在FFT应用中为什么要采用时间窗呢？

傅里叶变换(FFT)实现了时域到频域的转换，是信号分析中最常用的基本功能之一。本文将描述FFT应用中为什么要采用时间窗，以及RBW与时间窗的关系。

FFT变换是在一定假设下完成的，即认为被处理的信号是周期性的。图1给出了一正弦信号的采集样点波形，如果对Frame1作FFT运算，则会对其进行周期扩展。显然，在周期扩展的时候，造成了样点的不连续，样点不连续等同于相位不连续，相当于引入了相位调制，这将导致产生额外的频率成分，该现象称为频谱泄露。

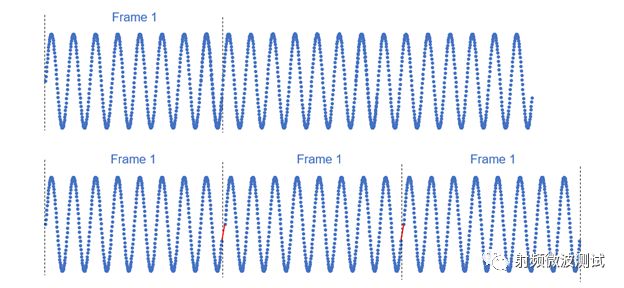
图1. 周期扩展引起样点的不连续

频谱泄露产生了原本信号中并不包含的频率成分，如图2所示，信号的频率本应只在虚线位置，但由于样点不连续，FFT之后导致产生了诸多频率点，如图所示的实线位置。频谱泄露会扰乱测试，尤其在观测小信号时，较强的频谱泄露成分可能淹没比较微弱的信号。

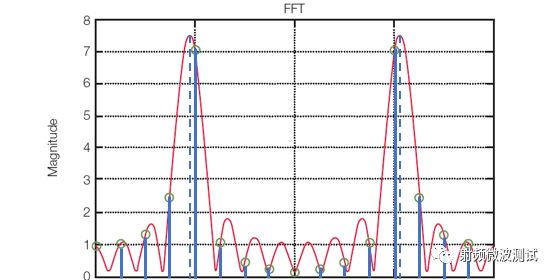
图2. 样点不连续引起频谱泄露

如何避免或者降低频谱泄露呢？这就需要使用下文介绍的时间窗(Window) 技术。

如果能够消除样点不连续，就可以消除频谱泄露。为了实现这一点，需要引入时间窗 (Window)，时间窗包含的样点数目与信号相同，而且两端的样点值通常为0。在FFT之前，时间窗与波形相乘，周期扩展后可以保证样点的连续性。

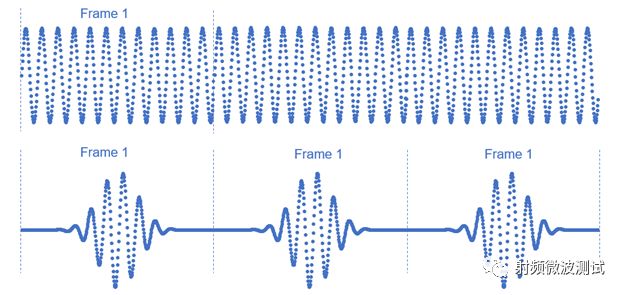
图3. 通过引入时间窗可改善频谱泄露

时间窗相当于一个滤波器，不同的时间窗具有不同的频响特性，比如边带抑制、矩形因子等，相应的幅度测试精度也不同。虽然基于FFT的频谱分析中没有IF filter，但是依然有RBW的概念，时间窗就决定了RBW的形状和大小。

RBW称为分辨率带宽，决定了频率分辨率，RBW越小，分辨率越高。RBW与时间窗宽度(即Window Time) 成反比，但即使时间窗宽度相同，不同的时间窗类型对应的RBW也不同，存在一个因子 k ，并满足如下关系：

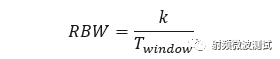
下面以矩形窗为例，RBW与时间窗宽度有什么关系呢？矩形窗的双边带频谱为 Sa(ω) 函数，如图4所示，假设窗口时间为T，则频率为** ±N*2π/T** (N为非零整数)处均为零点。矩形窗的双边带频谱可以写为如下表达式：

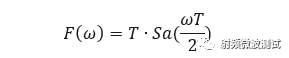
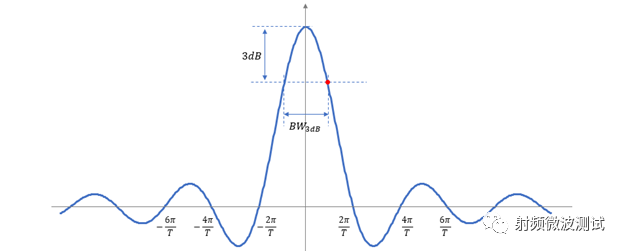
图4. 矩形窗的频谱特性(双边带频谱)

对于图4所示的频谱，相对峰值电平下降3dB的频点位于何处？从电压的角度讲，下降3dB的频点处，幅值将为峰值的 √2/2 。

简便起见，令sin(x)/x=√2/2 ，则x≈1.39 。经计算ω=2.78/T ，f=ω/2π≈0.443/T 。图4所示的频谱中，3dB带宽为：

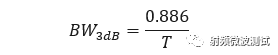
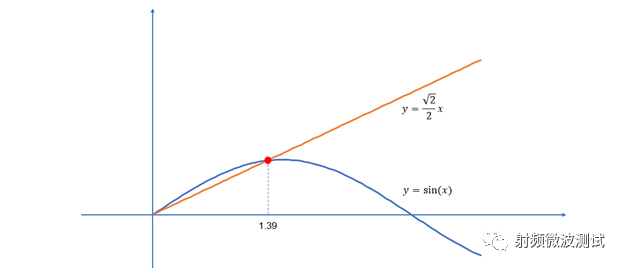
图5. x=1.39处，幅值下降3dB

如前所述，FFT应用中会将信号周期扩展，因此FFT是将信号当作一个周期信号来对待的。FFT得到的频点也是离散的，这些离散的频点称为freq. bin，两个相邻bin之间的频间距为扩展周期的倒数，扩展周期即为时间窗的宽度。bin间距决定了频率分辨率，间距越小，频率分辨率越高。

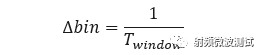
类似于扫频式频谱分析， FFT频谱分析中也有RBW****的概念，尽管不存在 IF filter 。 在****FFT 频谱分析中， RBW决定于时间窗幅频特性的3dB 带宽。 不同的时间窗类型，具有不同的****RBW 表达式。 对于矩形窗， RBW****为

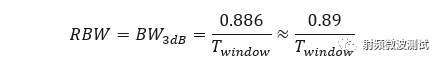
从上式可以看出，同是表征频率分辨率的参数，矩形窗的RBW并不等于bin间距，而是小于bin间距。频谱分析应用中通常提及RBW，但RBW与bin间距存在如下关系

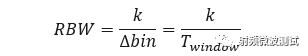
常见的时间窗类型包括：

Kaiser、Rectangular、Hamming、Hanning、Blackman-Harris、Flat-Top等。下图给出了不同时间窗类型对应的k因子大小。不同的时间窗，频谱泄露、幅度测试精度及RBW均不同，测试时应该如何选择呢，后文将有详细介绍。

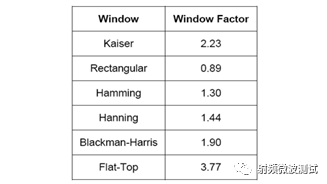
图6. 不同时间窗类型对应的k因子不同