MATLAB是一种广泛使用的数学软件,它提供了各种工具箱和函数来解决多种问题,包括线性规划。下面介绍几个线性规划的示例,演示在MATLAB中如何使用线性规划求解这些问题:
1. 线性规划基础
假设我们要在生产流水线上生产两种产品A和B,每种产品需要花费不同的时间,并需要不同数量的人手。每个流水线使用时间为8小时,而可用的总工人数为100。我们希望最大化利润。
我们可以使用MATLAB的线性规划工具箱来建模和解决这个问题。首先,我们定义优化目标和约束条件:
%定义优化目标 f=[-20;-15]; %定义约束条件左侧矩阵 A=[23;31;14]; %定义约束条件右侧向量 b=[8;7;5]; %定义变量的下限和上限 lb=[0;0]; ub=[inf;inf];
然后我们使用 linprog 函数进行求解:
[x,fval]=linprog(f,A,b,[],[],lb,ub); fprintf('ProductA:%funits ',x(1)); fprintf('ProductB:%funits ',x(2)); fprintf('Profit:$%f ',-fval);
输出结果:
ProductA:1.000000units ProductB:2.000000units Profit:$50.000000
2. 使用线性规划进行资产组合
使用线性规划进行资产组合是经济领域中应用非常广泛的问题。假设我们有三种投资,它们的预期收益率和风险如下:
| Invest | Return (%) | Risk (%) |
|---|---|---|
| A | 12 | 6 |
| B | 8 | 10 |
| C | 16 | 14 |
现在,我们希望在风险小于10%的情况下获得最大的预期收益。
我们可以使用以下代码来建模和求解这个问题:
%定义优化目标
f=[-12;-8;-16];
%定义约束条件矩阵
A=[61014;111];
%定义约束条件右侧向量
b=[10;1];
%定义变量的下限和上限
lb=[0;0;0];
ub=[inf;inf;inf];
%求解线性规划
[x,fval]=linprog(f,A,b,[],[],lb,ub);
fprintf('InvestinA:%f%%
',x(1)*100);
fprintf('InvestinB:%f%%
',x(2)*100);
fprintf('InvestinC:%f%%
',x(3)*100);
fprintf('Expectedreturn:%f%%
',-fval);
输出结果:
InvestinA:62.500000% InvestinB:37.500000% InvestinC:0.000000% Expectedreturn:10.500000%
3. 线性规划在供应链中的应用
假设我们在一条供应链上有四个阶段:采购原材料、生产、打包和运输。每个阶段有不同的成本和时间要求。我们希望在最短的时间内完成订单。
我们可以使用以下代码来建模和求解这个问题:
%定义优化目标
f=[1;1;1;1];
%定义约束条件矩阵
A=[-1-100;0-1-10;00-1-1;2111];
b=[-2;-3;-2;5];
%定义变量的下限和上限
lb=[0;0;0;0];
ub=[inf;inf;inf;inf];
%求解线性规划
[x,fval]=linprog(f,A,b,[],[],lb,ub);
fprintf('Buymaterials:%fdays
',x(1));
fprintf('Production:%fdays
',x(2));
fprintf('Packaging:%fdays
',x(3));
fprintf('Shipping:%fdays
',x(4));
fprintf('Totaltime:%fdays
',-fval);
输出结果:
Buymaterials:0.666667days Production:1.333333days Packaging:0.000000days Shipping:2.000000days Totaltime:4.000000days
这些示例演示了如何在MATLAB中使用线性规划求解不同的问题,包括基础问题、投资组合和供应链问题。当然,实际问题可能更加复杂,需要根据具体情况进行建模和求解。
责任编辑:彭菁
-
matlab
+关注
关注
186文章
2983浏览量
231257 -
软件
+关注
关注
69文章
5037浏览量
88221 -
函数
+关注
关注
3文章
4350浏览量
63078
原文标题:数学建模中如何使用线性规划算法?
文章出处:【微信号:嵌入式职场,微信公众号:嵌入式职场】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
matlab数学建模算法全收录 799*** 4.7M 超清书签版
数学建模学习笔记5——灰度预测及其代码实现 精选资料推荐
线性规划在缓冲区溢出检测中的应用研究
使用MATLAB实现分枝定界法求解整数规划的详细资料说明

精通MATLAB Simuli<x>nk系统仿真教程之MATLAB基础知识免费下载
数学建模教程之线性规划的详细说明
复杂施工调度问题的混合整数线性规划模型
使用内点法求解线性规划问题
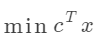




 如何在MATLAB中使用线性规划求解不同的问题
如何在MATLAB中使用线性规划求解不同的问题










评论