在 飞行器姿态计算 中,卡尔曼滤波是最常用的姿态计算方法之一。今天就以目前的理解讲以下卡尔曼滤波。
先用一个日常生活中的例子来解释下卡尔曼滤波。
假设你正在驾驶一辆汽车并使用 GPS 导航系统。然而,你可能会注意到,GPS 定位有时会出现一些误差,导致导航系统显示的位置与实际位置存在差异。卡尔曼滤波就可以用来解决这个问题。
在这个例子中,我们可以将卡尔曼滤波器视为一种数据处理技术,用于融合 GPS 定位数据和车辆本身的运动模型,从而更准确地估计车辆的位置和速度。
卡尔曼滤波器的基本原理如下:
- 预测(预测状态):根据车辆的运动模型和上一时刻的位置和速度信息,使用预测方程预测当前时刻的位置和速度。这个预测是基于物理规律进行的,假设车辆在没有外界干扰的情况下按照一定的运动模型移动。
- 更新(更新状态):根据 GPS 定位系统提供的测量数据(位置数据),使用更新方程将预测值与测量值进行比较,并根据测量的准确性来权衡两者。如果 GPS 测量准确,卡尔曼滤波器会更加相信测量值;如果 GPS 测量存在误差或不可靠,卡尔曼滤波器会更加相信预测值。
- 合并(状态合并):通过组合预测和更新步骤得到的信息,卡尔曼滤波器会生成一个新的状态估计,该估计综合考虑了车辆运动模型和 GPS 测量数据的信息。
- 迭代:上述步骤会不断地重复进行,每次利用新的测量数据和先前的状态估计进行预测和更新,以不断优化对车辆位置和速度的估计。
卡尔曼滤波器利用过去的信息(运动模型)和当前的观测数据(GPS 测量)来进行状态估计,通过动态调整预测和更新之间的权衡,以获得更准确和稳定的估计结果。
在汽车导航系统中,卡尔曼滤波器可以帮助消除 GPS 定位的误差,提供更准确的位置和速度信息,从而改善导航准确性和用户体验。
再举一个跟加速度计和陀螺仪有关的例子,以帮助我们更好地理解卡尔曼滤波的工作原理。
想象一下,你正在玩一款虚拟现实游戏,需要通过头戴式显示器(VR 头盔)来体验沉浸式的游戏世界。然而,由于头戴式显示器的内置传感器的测量存在一些噪声和误差,导致你在游戏中的头部姿态(旋转角度)的准确性受到影响。
在这个情景中,卡尔曼滤波器可以用来改善头部姿态的估计,提供更平滑和准确的旋转角度数据,从而增强游戏的沉浸感和真实感。
以下是卡尔曼滤波在这个例子中的具体应用步骤:
- 传感器测量:VR 头盔内置了陀螺仪传感器,用于测量头部的旋转角速度。这些测量值包含一定的噪声和误差。
- 预测(预测姿态):利用上一时刻的姿态信息和陀螺仪测量的角速度,使用预测方程来预测当前时刻的头部姿态。预测方程基于物理模型,假设头部在没有外界干扰的情况下按照一定的运动规律旋转。
- 更新(更新姿态):通过 VR 头盔的其他传感器,例如加速度计和磁力计,测量头部的加速度和磁场信息。利用更新方程,将预测的姿态与这些测量值进行比较,并根据测量的准确性来调整预测和测量之间的权衡。
- 合并(姿态合并):通过综合预测和更新步骤得到的信息,卡尔曼滤波器会生成一个新的头部姿态估计,该估计综合考虑了陀螺仪、加速度计和磁力计的测量数据以及物理模型的信息。
- 迭代:上述步骤会不断地重复进行,每次利用新的测量数据和先前的姿态估计进行预测和更新,以不断优化对头部姿态的估计。
通过卡尔曼滤波器的迭代过程,头戴式显示器可以更准确地估计你的头部姿态,使得虚拟现实游戏中的画面更加平滑和真实,增强了游戏的沉浸感。
下面用一个简化版的代码作为示例,增进我们对卡尔曼滤波算法的理解:
import numpy as np
# 初始化卡尔曼滤波器参数
dt = 0.01 # 时间步长
A = np.array([[1, -dt],
[0, 1]]) # 状态转移矩阵
H = np.array([[1, 0]]) # 观测矩阵
Q = np.array([[0.01, 0],
[0, 0.01]]) # 状态噪声协方差
R = np.array([[0.1]]) # 观测噪声协方差
# 初始化状态变量和协方差矩阵
x = np.array([[0],
[0]]) # 初始状态(姿态角度和角速度)
P = np.array([[1, 0],
[0, 1]]) # 初始协方差矩阵
# 模拟姿态测量数据
measurements = [0.1, 0.12, 0.08, 0.09, 0.11]
# 使用卡尔曼滤波进行姿态估计
filtered_measurements = []
for measurement in measurements:
# 预测步骤
x = np.dot(A, x)
P = np.dot(np.dot(A, P), A.T) + Q
# 更新步骤
y = measurement - np.dot(H, x)
S = np.dot(np.dot(H, P), H.T) + R
K = np.dot(np.dot(P, H.T), np.linalg.inv(S))
x = x + np.dot(K, y)
P = np.dot((np.eye(2) - np.dot(K, H)), P)
# 将滤波后的姿态估计结果保存到列表中
filtered_measurement = x[0, 0]
filtered_measurements.append(filtered_measurement)
# 打印每个步骤的结果
print("测量值:", measurement)
print("预测状态:", x)
print("预测协方差:", P)
print("滤波后的姿态估计:", filtered_measurement)
print("--------")
# 打印滤波后的姿态估计结果
print("滤波后的姿态估计结果:", filtered_measurements)
- 初始化:在卡尔曼滤波的开始时,需要初始化状态变量和协方差矩阵。状态变量表示系统的状态,对于头部姿态估计,可以包括姿态角度和角速度。协方差矩阵表示状态变量的不确定性。
在代码示例中,我们使用x表示状态变量,其中x[0]表示姿态角度,x[1]表示角速度。P是状态协方差矩阵,初始时给定一个较大的值表示对状态变量的不确定性的估计。 - 预测(预测状态):在卡尔曼滤波的预测步骤中,根据系统的动力学模型和上一时刻的状态变量,使用预测方程来估计当前时刻的状态。
在代码示例中,我们使用状态转移矩阵A和上一时刻的状态变量x,通过矩阵乘法运算来计算当前时刻的预测状态x。预测方程基于物理模型,假设系统在没有外界干扰的情况下按照一定的运动规律变化。 - 更新(更新状态):在卡尔曼滤波的更新步骤中,使用观测数据来校正预测的状态,以提高估计的准确性。
在代码示例中,我们通过观测矩阵H将预测状态映射到观测空间,并将观测值与预测状态进行比较,得到观测残差(测量误差)。然后,通过计算协方差矩阵P和观测噪声协方差矩阵R的乘积,并进行一系列矩阵运算,计算卡尔曼增益K。卡尔曼增益表示预测值和观测值之间的权衡,用于将观测残差应用到预测状态上。
最后,通过将卡尔曼增益乘以观测残差,并将结果添加到预测状态上,得到更新后的状态估计x。 - 合并(状态合并):在卡尔曼滤波的合并步骤中,通过综合预测和更新步骤得到的信息,生成新的状态估计。
在代码示例中,我们通过计算P和卡尔曼增益K的乘积,并将其与单位矩阵的差异进行矩阵运算,得到更新后的协方差矩阵P。最后,我们返回状态估计中的姿态角度部分x[0, 0]作为滤波后的姿态估计结果。 - 迭代:上述步骤会不断地重复进行,每次使用新的观测数据和先前的状态估计进行预测和更新,以不断优化对姿态的估计。
在代码示例中,我们通过一个循环将多个观测值传递给卡尔曼滤波器,并获得滤波后的姿态估计结果。
请注意,实际应用中可能会涉及更复杂的模型和参数调整。上述代码示例仅提供了卡尔曼滤波的基本框架和实现思路,具体的实现细节可能会因应用场景而有所不同。
卡尔曼滤波算法应用非常广泛,算法背后的解决问题的思想是我们应该学习的核心。
-
传感器
+关注
关注
2548文章
50664浏览量
751893 -
滤波器
+关注
关注
160文章
7727浏览量
177668 -
飞行器
+关注
关注
13文章
716浏览量
45468 -
卡尔曼滤波
+关注
关注
3文章
162浏览量
24634
发布评论请先 登录
相关推荐
浅析卡尔曼滤波原理




 浅析卡尔曼滤波
浅析卡尔曼滤波
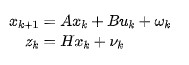











评论