使用信赖域法求解无约束优化问题
在 MATLAB 中,可以使用 fminunc 函数来求解无约束优化问题,其中包括信赖域法。fminunc 函数的使用方法非常灵活,可以通过修改参数来指定不同的算法、梯度计算方法等。
以下是一个使用信赖域法求解无约束优化问题的简单示例:
假设有以下无约束优化问题:
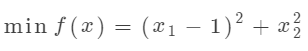
下面是 MATLAB 的代码实现:
%定义目标函数和梯度函数 f=@(x)(x(1)-1)^2+x(2)^2; grad_f=@(x)[2*(x(1)-1);2*x(2)]; %定义初始点和参数 x0=[0;0]; options=optimoptions('fminunc','Display','iter','Algorithm','trust-region'); %调用fminunc函数进行优化 [x,fval,eflag,output,grad,hessian]=fminunc(f,x0,options);
在上面的代码中,首先定义了目标函数 f 和梯度函数 grad_f,然后调用 fminunc 函数来求解优化问题。需要注意的是,信赖域法需要计算 Hessian 矩阵,因此需要将 fminunc 函数的输出参数中的 Hessian 矩阵 hessian 提取出来。如果不需要计算 Hessian 矩阵,可以通过将 fminunc 函数的参数 'Hessian','off' 来禁用 Hessian 计算。
信赖域法还有一些其他的参数可以调整,例如信赖域半径、最大迭代次数、收敛容限等。我们可以通过修改 options 结构体中的参数来指定不同的值。在上面的代码中,我们指定了 Algorithm 为 'trust-region',即使用信赖域法求解无约束优化问题,默认情况下 fminunc 函数使用拟牛顿法进行优化。
需要注意的是,信赖域法需要计算目标函数的梯度,因此要确保梯度函数的正确性。如果没有提供梯度函数,则 fminunc 函数会通过自动微分方法计算梯度。
审核编辑:汤梓红
-
matlab
+关注
关注
186文章
2984浏览量
231306 -
函数
+关注
关注
3文章
4350浏览量
63106 -
约束
+关注
关注
0文章
82浏览量
12791
原文标题:使用信赖域法求解无约束优化问题
文章出处:【微信号:嵌入式职场,微信公众号:嵌入式职场】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
matlab中无约束非线性规划函数\fminunc函数使用方法
优化入门绝顶精品!!!
机器学习基础|深入理解拉格朗日乘子法
Modelsim不支持无约束的记录
基于改进DE算法的难约束优化问题的求解
MATLAB软件在机械优化设计中的应用
Fluke详述如何定位并解决无约束AP的问题
一种改进灰狼优化算法的用于求解约束优化问题




 使用信赖域法求解无约束优化问题
使用信赖域法求解无约束优化问题











评论