MATLAB®是一个强有力的工具,可用来快速分析从模数转换器(ADC)输出所捕获的数据。本应用笔记演示了如何使用MATLAB来突破逻辑分析仪存储深度的局限。描述并比较了三种数码拼接方式(基本,超前和反转)。并给出了三种方法所得的结果。
介绍
要评估一个高速模数转换器(ADC)的性能,就需要捕获其数字输出码,然后进行分析。逻辑分析仪的存储深度常常成为一个重要局限,妨碍系统捕获足够的数据点,以生成高分辨率FFT,或者精确的INL/DNL图。解决该问题的一个简单办法是使用某种数学工具,例如MATLAB ( 图1 ),将多组数据连接起来。连接数据的一个缺点是,通常会在两组数据之间的连接点出现很大的不连续性。尽管不连续性对INL/DNL图的影响极小,但对高分辨率FFT而言,几乎是毁灭性的( 图2 )。
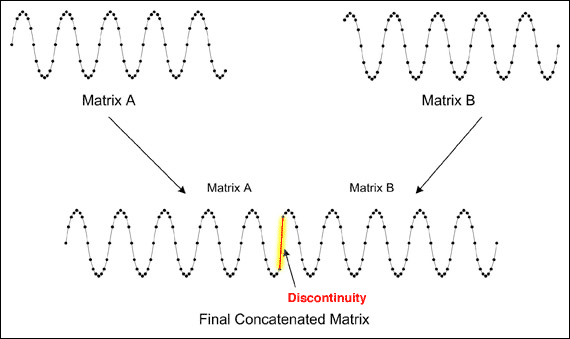
图1. 连接后的数据在两组数据之间出现不连续。
![图2. a) 捕获单组16384点数据并分析;b) 捕获两组8192点数据,连接,然后分析“拼接”技术。]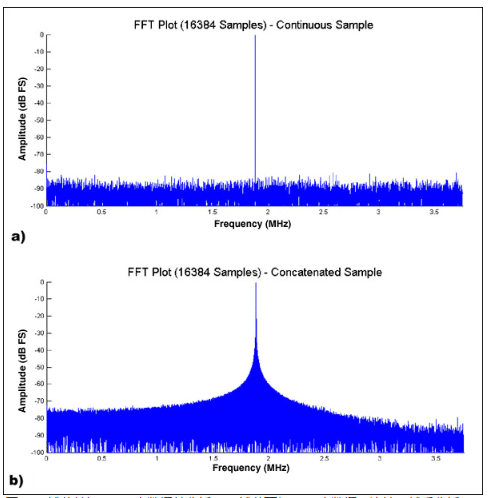
图2. a) 捕获单组16384点数据并分析;b) 捕获两组8192点数据,连接,然后分析“拼接”技术。
有一种办法可以消除不连续性,就是在各组数据中寻找相同的点簇(一般为3到4个点),然后在这些点将两组数据“拼接”在一起( 图3 )。最简单的“拼接”方法是,记录下第一组数据中的最后四个点,然后在第二组数据里寻找相同的点簇。相同点簇出现在第二组数据中的位置称为“拼接点”。第二组数据中在拼接点之前的所有数据均被舍弃;第二组数据中的剩余部分与第一组数据合并。这种技术即所谓的基本数码拼接,实现起来非常简单,可以在MATLAB中非常快地运行。
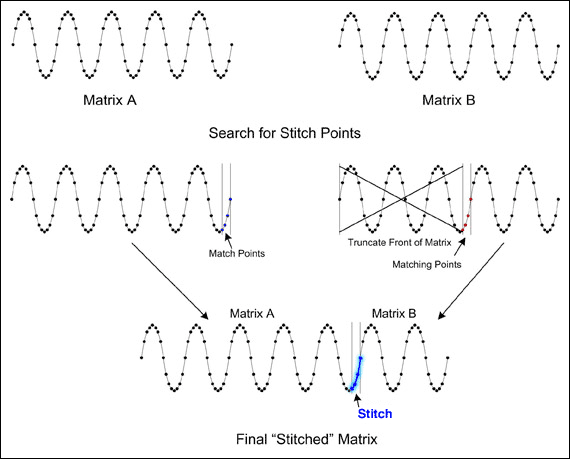
图3. 基本数码拼接后得到的最终“拼接”数组。
采用基本拼接方法拼接数据时,有时必须丢掉第二组数据中的近一半,才能找到与第一组数据最后四个点相匹配的一簇点。作为另一种选择,丢掉第一组数据尾部的几个点,常常有助于找到更靠近第二组数据起点的拼接点( 图4 )。然而,通过丢掉第一组数据尾部、第二组数据头部的部分采样点来寻找匹配点的方法实现起来比较困难。这种处理被称为超前数码拼接。理想拼接点应该能够保留尽可能多的数据点,寻找这样的拼接点需要认真的考虑和一定的编程技巧。正确地实现之后,超前拼接技术通常能够得到两组小数组所含数据点总数的至少90%。
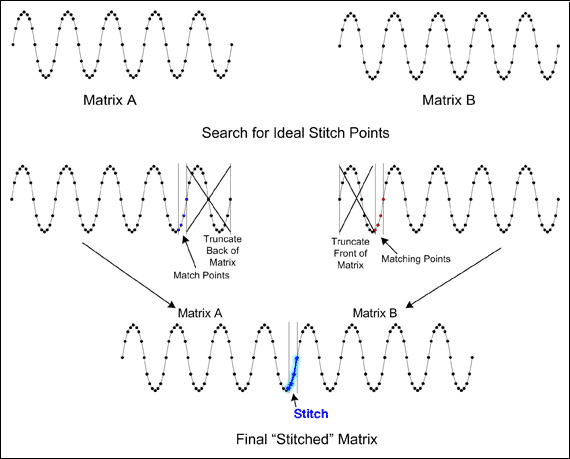
图4. 采用超前拼接技术寻找理想拼接点,最终得到“拼接”后的数组。
将第二组数据(数组B)拼接到第一组数据(数组A)之前被称为反转拼接,这种方式有可能得到更大的拼接数组( 图5 )。但是,这种技术会使处理时间翻倍,因为必须在A领先于B和B领先于A两种情况下寻找拼接点。此外,当与其他拼接技术一起使用时,反转拼接方式所带来的好处通常很少。因此,对于较慢的PC,反转拼接技术大幅度增加的处理时间开销较之它所带来的好处而言并不太值。表1详细比较了这三种代码拼接方法。
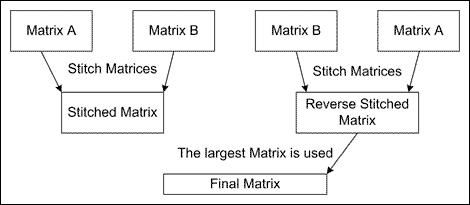
图5. 反转拼接的处理时间加倍,但常常收效甚微。
表1. 三种拼接技术对比 *
| Stitch Technique | Size of Final Data Set | Description |
|---|---|---|
| Data Set Numbers | # of codes(averaged) | % of two data sets(averaged) |
| 1 + 2 | 3 + 4 | 1 + 4 |
| Concatenate† | N/A | 16384 |
| Basic | 11060 | 8192‡ |
| Reverse | 11060 | 8192‡ |
| Advanced | 13790 | 16046 |
| Advanced+Reverse | 15427 | 16176 |
*采用上述拼接技术对两组8K (8192个)数据进行拼接。为确保准确性,采用四组8192点数据(分别编号为1至4)重复本测试。每组测试所合成的数据取平均后列于测试数据的右侧。
† 直接连接总能得到100%的数据。
‡ 无法拼接数据。### MATLAB函数说明
本文后附的MATLAB代码(附录A和B中的StitchMatrices和FindStitchPoint)将上述论点结合到一个易于使用的函数中。这些函数可接受两组数据(MATLAB中的单列矩阵)和几个输入变量(用来选择超前/反转拼接功能)。FindStitchPoint例程用来确定拼接点在数组A和B中的偏移量。StitchMatrices例程则根据FindStitchPoint例程给出的偏移量对两组数据A和B进行舍弃和组合。同时,最终数据的拼接点被记录在PrevStitchBins数组中,以便于后续处理。当拼接多组数据时,PrevStitchBins可保存老的拼接点。
结论
拼接两组数据可以得到一组理想的结果。图6给出了三组8192点数据使用上述拼接技术拼接起来(使用5个拼接点)后的FFT图。所得的FFT几乎与前面图2a所示,基于16384个连续点所得结果相同。
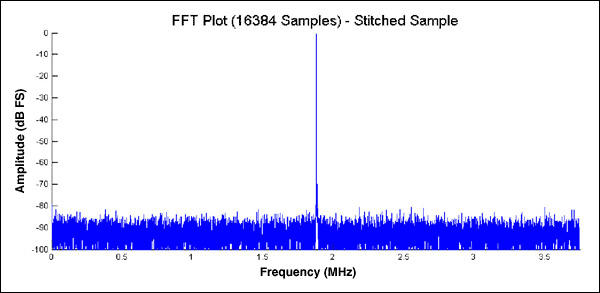
图6. 数码拼接后得到精确的FFT图。
审核编辑:郭婷
-
matlab
+关注
关注
185文章
2976浏览量
230464 -
adc
+关注
关注
98文章
6498浏览量
544627
发布评论请先 登录
相关推荐
逻辑分析仪是什么
RAM内存不足错误
逻辑分析仪内存不足?“拼”出解决之道




 逻辑分析仪内存不足? “拼”出解决之道!
逻辑分析仪内存不足? “拼”出解决之道!










评论