MATLAB是一个数学软件,它对矩阵运算、线性方程组求解、特征值与特征向量等方面提供了强大的支持。
1. 矩阵运算
在MATLAB中,可以用矩阵和向量来存储数据,并进行向量和矩阵的加减乘除以及转置、逆、行列式等操作。例如,要对两个矩阵A和B进行乘法运算,可以使用“*”符号:
C = A * B
其中,C为运算结果。此外,还可以使用“+”、“-”、“'”等符号进行加减法和转置运算。
2. 线性方程组求解
在MATLAB中,当需要解决线性方程组时,可以使用:
x = A b
其中,x为未知变量的解向量。此外,还可以使用“inv()”函数求解矩阵的逆,但需要注意逆不存在或不唯一的情况。
3. 特征值与特征向量
在MATLAB中,可以使用“eig()”函数来求解矩阵的特征值和特征向量。例如,对于矩阵A,可以写成:
[V, D] = eig(A)
其中,V为特征向量矩阵,D为特征值对角矩阵。此外,还可以使用“det()”函数求解矩阵的行列式,但需要注意行列式为0的情况。
综上所述,MATLAB提供了强大的矩阵运算、线性方程组求解以及特征值与特征向量求解等支持,对于处理数学计算和数据分析具有非常重要的作用。
矩阵运算示例
创建两个矩阵A和B:
A=[12;34]; B=[56;78];
计算A与B的乘积:
C=A*B
计算A加上B的转置的结果:
D=A+B'
线性方程组求解示例
假设有一个包含3个未知数的线性方程组:
2x-y+3z=6 x+y+2z=4 3x-2y+z=2
将其转换成矩阵形式:
A=[2-13;112;3-21]; b=[6;4;2];
使用MATLAB求解:
x=Ab
得到的结果为:
x= 1.0000 -1.0000 2.0000
表示未知数x、y、z分别为1、-1、2。
特征值与特征向量示例
假设有一个矩阵:
A=[123;456;789];
使用MATLAB求解其特征值和特征向量:
[V,D]=eig(A)
得到的结果为:
V= -0.231970687246286-0.7858302387426290.408248290463863 -0.525322093301234-0.086751339519221-0.816496580927726 -0.8186734993561830.6123275597041870.408248290463863 D= -1.1168e-1500 0-1.0000e+000 001.1168e+01
其中,V表示特征向量矩阵,D表示特征值对角矩阵。可以看到,特征值为0、-1、11,特征向量分别为三列V矩阵。
另外,如果想要对矩阵的行列式进行求解,可以使用“det()”函数。例如:
det(A)
得到的结果为:
ans= 0
表示该矩阵的行列式为0,即该矩阵不可逆。
审核编辑:汤梓红
-
matlab
+关注
关注
186文章
2983浏览量
231258 -
矩阵
+关注
关注
0文章
425浏览量
34678 -
函数
+关注
关注
3文章
4350浏览量
63079 -
线性方程组
+关注
关注
0文章
3浏览量
986
原文标题:matlab矩阵运算、线性方程组求解、特征值与特征向量
文章出处:【微信号:嵌入式职场,微信公众号:嵌入式职场】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
MATLAB应用求线性方程组的通解
matlab求解非线性方程组问题
labview 将矩阵的特征值排序,再把排序后的特征值对应的特征向量组成矩阵
labview求解非线性方程组
求解矩阵特征值及特征向量的新方法
线性方程组并行迭代解法的新思路
迭代矩阵特征值模的界
使用MATLAB编程实现里查森迭代法线性方程组求解的资料和程序免费下载




 MATLAB矩阵运算、线性方程组求解、特征值与特征向量
MATLAB矩阵运算、线性方程组求解、特征值与特征向量
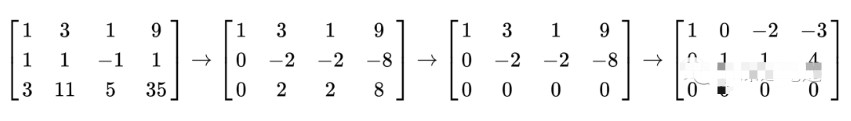










评论