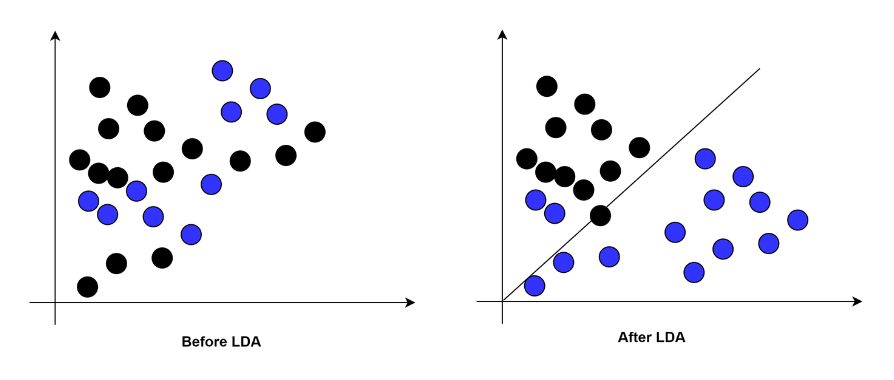
LDA(Linear Discriminant Analysis)是一种经典的线性分类方法,它的基本思想是将高维数据映射到低维空间中,同时最大化不同类别之间的距离和最小化同类别之间的距离,以此来达到降维和分类的目的。
具体来说,LDA 将数据分为不同的类别,并计算它们的均值和协方差矩阵。然后,它使用这些统计量来计算一个投影矩阵,将原始数据投影到一个新的低维空间中,使得不同类别的投影之间距离最大化,而同类别之间距离最小化。
在 MATLAB 中,可以使用 Classification Learner App 或 fitcdiscr 函数来进行 LDA 分析。以下是一个示例代码,假设我们有一个包含 1000 个样本和 10 个特征的数据集,并且有两个类别:
%生成随机数据 data=[randn(500,10)+1;randn(500,10)-1]; labels=[ones(500,1);ones(500,1)*2]; %计算LDA lda=fitcdiscr(data,labels); %可视化结果 gscatter(data(:,1),data(:,2),labels); holdon; line(lda.Mu(1,:),lda.Mu(2,:),'LineWidth',2,'Color','k'); line([lda.Coeffs(1,1).Constlda.Coeffs(1,2).Const]+... [lda.Coeffs(1,1).Linearlda.Coeffs(1,2).Linear]*[-44],... [lda.Coeffs(1,1).Constlda.Coeffs(1,2).Const]+... [lda.Coeffs(1,1).Linearlda.Coeffs(1,2).Linear]*[-44],... 'LineWidth',2,'Color','r'); line([lda.Coeffs(2,1).Constlda.Coeffs(2,2).Const]+... [lda.Coeffs(2,1).Linearlda.Coeffs(2,2).Linear]*[-44],... [lda.Coeffs(2,1).Constlda.Coeffs(2,2).Const]+... [lda.Coeffs(2,1).Linearlda.Coeffs(2,2).Linear]*[-44],... 'LineWidth',2,'Color','b'); axisequal; holdoff;
其中,fitcdiscr 函数可以计算 LDA,并返回一个 ClassificationDiscriminant 对象。这个对象包含投影矩阵、均值和协方差矩阵等信息。我们可以使用这些信息来进行分类或对新数据进行投影。
以上代码中的 gscatter 函数用于可视化数据,而 line 函数则用于绘制分界线和均值点。
综上所述,LDA 是一种非常有效的降维和分类方法,可以在不丢失太多信息的情况下将高维数据降到低维空间中,并且能够在低维空间中进行有效的分类。在 MATLAB 中,可以使用 Classification Learner App 或 fitcdiscr 函数来进行 LDA 分析。
责任编辑:彭菁
-
函数
+关注
关注
3文章
4327浏览量
62567 -
线性
+关注
关注
0文章
198浏览量
25145 -
LDA
+关注
关注
0文章
29浏览量
10605
原文标题:LDA经典的线性分类方法
文章出处:【微信号:嵌入式职场,微信公众号:嵌入式职场】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
LDA $88,SP完全不懂啊
基于LDA的SIFT算法在图像配准中的应用
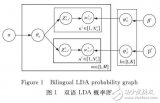
基于双语LDA的跨语言文本相似度计算方法
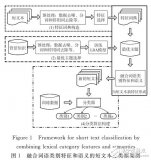
融合词语类别特征和语义的短文本分类方法
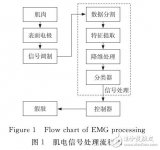
基于LDA分类器的模式识别方法
人脸识别经典算法三:Fisherface(LDA)
基于Hadoop平台的LDA算法的并行化实现

基于隐含狄列克雷分配LDA分类特征扩展的广告过滤方法
一种融合图像纹理结构信息的LDA扣件检测模型
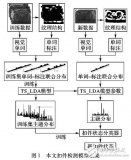
基于监督局部线性嵌入的中药材分类鉴别研究
用PCA还是LDA?特征抽取经典算法大PK
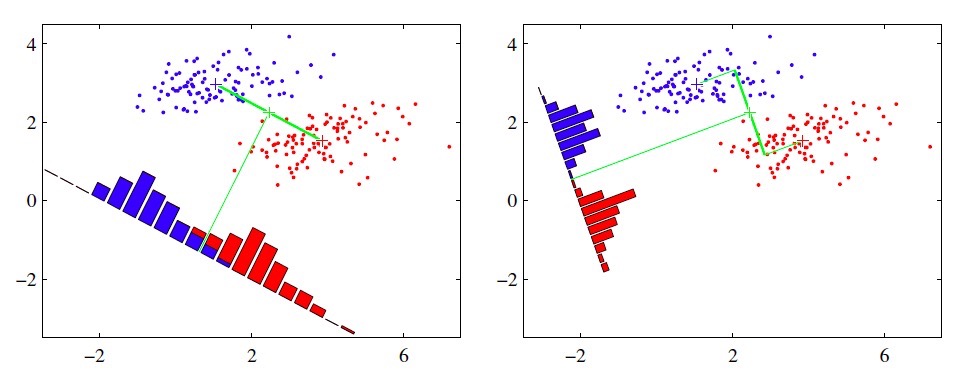
一种捕获主题单词信息的主题模型JEA-LDA




 基于LDA经典的线性分类方法
基于LDA经典的线性分类方法










评论