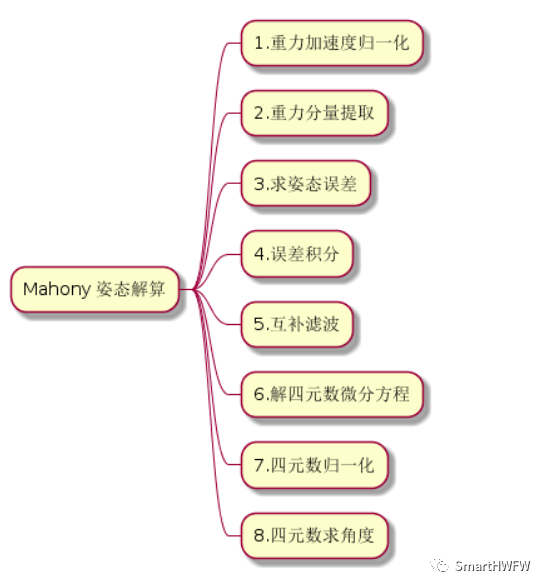
1.概述
在进行代码分析之前,了解Mahony滤波器的原理和公式推导是必要的。Mahony滤波器是一种基于四元数的姿态估计滤波器,其主要思想是通过加速度计和陀螺仪的测量值来估计姿态,并通过四元数来表示姿态。其公式推导涉及到四元数的运算和旋转矩阵的推导,需要具备一定的数学基础和姿态估计相关的知识。
四元数是一种数学工具,它可以用来表示三维空间的旋转信息。在秦永元的《惯性导航》这本书第9.2章节中,介绍了姿态更新计算的四元数算法,其中详细讲解了四元数的概念、四元数与姿态阵之间的关系以及四元数微分方程。阅读完9.2章节的推导后,我们可以更深入地理解四元数的应用和原理。
之前我也写过一篇 《MEMS_惯性传感器09 - Mahony姿态解算算法详解》,但是还是建议阅读秦永元的《惯性导航》,这样更容易理解。
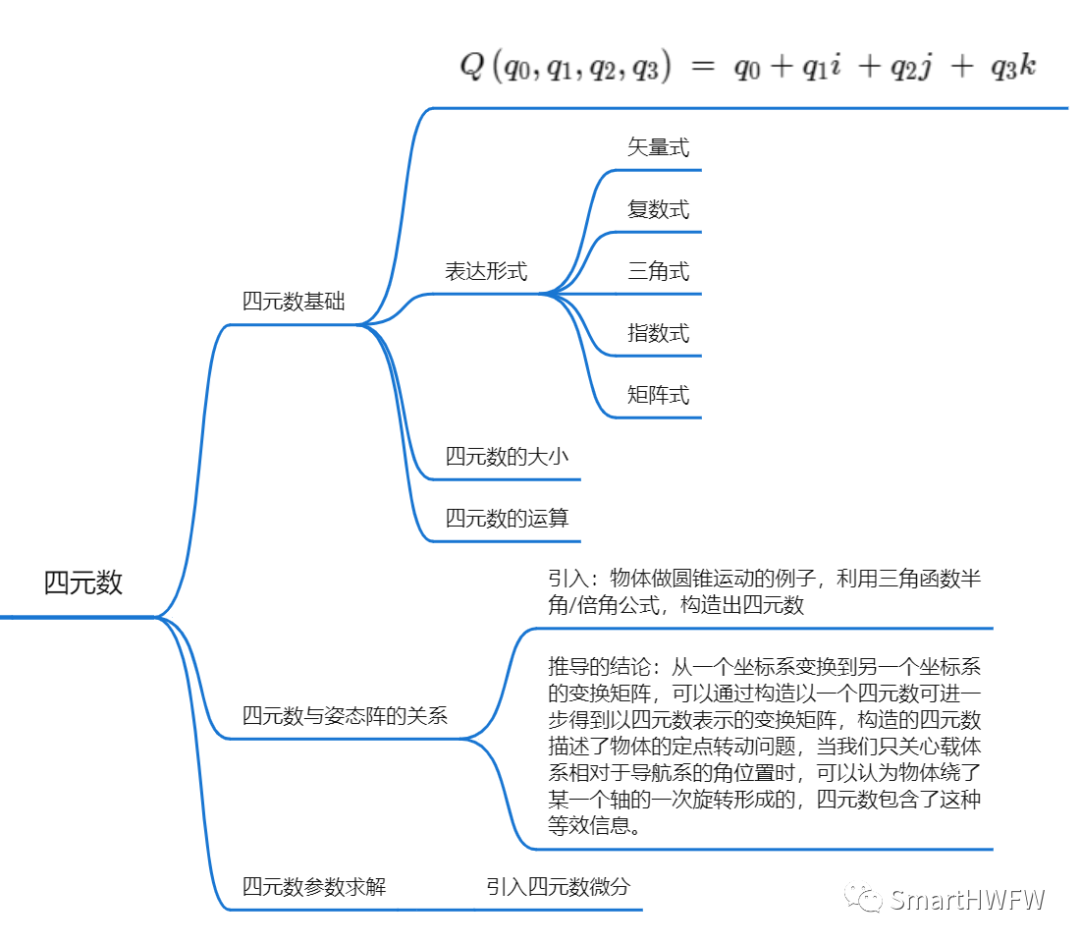
物体的姿态变化可以等效为绕某个轴的一次旋转。我们不需要关注物体变化的中间过程,只需要找到一种变换关系,就能够求出物体从导航坐标系到载体坐标系或从载体坐标系到导航坐标系的坐标。因此,我们需要推导出这种变化关系。
利用四元数与姿态阵的关系,可以推导得到如下结论:
(1) 四元数 Q (表达式如下) 描述了物体的定点转动,即,当之关心 b 系(载体系)相对于 R 系(导航系)的角位置时,可认为 b 系是由 R系经过无中间过程的一次性等效旋转形成的。
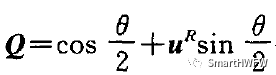
Q包含了这种等效旋转的全部信息;u^R 为旋转瞬间和旋转方向 θ为旋转过的角度
(2) 四元数可以确定出 b 系至 R 系的坐标变换矩阵
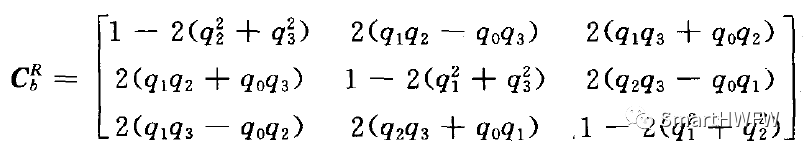
根据上述推导,已经得到了姿态变换矩阵和四元数表示法中的姿态角。然而,目前四元数的具体数值未知。为了得到真正的姿态角,需要找到确定四元数数值的方法。
通过已知的陀螺仪和加速度计获得的角速度和加速度,我们可以利用四元数微分来求解四元数的具体数值。四元数微分是指将四元数看作一个向量,然后对其进行微分,得到一个表示四元数变化率的向量。通过对四元数微分的计算,可以得到四元数的具体数值。
通过解微分方程,可以计算四元数的参数
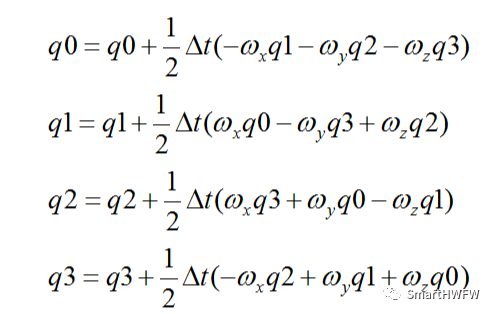
以上公式的推导过程已在书中详细说明,故本文不再赘述。针对误差消除,本文采用了Mahony滤波算法,该算法是本文的核心内容。
2.陀螺仪误差的消除
角度测量中存在偏差,由于角速度是积分得到的,陀螺仪获得的角速度信息存在小的偏差,积分后误差会不断累积,导致角度测量结果偏差较大。虽然加速度计获得的角度信息不会出现偏差,但其受噪声影响较大,短时间内可靠性不高。因此,我们可以利用加速度计获得的角度信息去矫正陀螺仪获得的姿态信息,从而消除算出来的角度误差。
核心思想是利用加速度计获取信息来补偿陀螺仪的角速度信息。具体实现步骤如下:
1.获取加速度的值,并对其归一化 (归一化是为了确保姿态变化矩阵中的四元数是规范四元数,并且利用陀螺仪更新的四元数也需要归一化。以确保与其他数据对应)
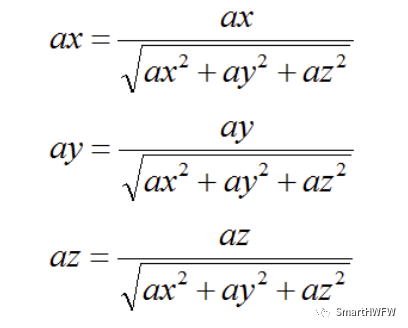
//Normaliseaccelerometermeasurement recipNorm = invSqrt(ax * ax + ay * ay + az * az); ax *= recipNorm; ay *= recipNorm; az *= recipNorm;
2.获取陀螺仪算出的姿态矩阵中的重力分量, 重力分量记为Vx、Vy、Vz
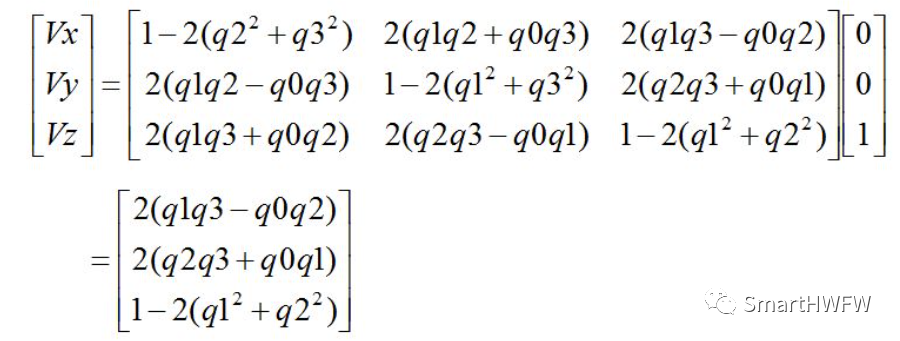
// Estimated direction of gravity and vector perpendicular to magnetic flux halfvx = q1 * q3 - q0 * q2; halfvy = q0 * q1 + q2 * q3; halfvz = q0 * q0 - 0.5f + q3 * q3;
3.获取姿态误差,(将第一步中 获取的重力向量归一化后的值与提取的姿态矩阵的重力向量叉乘)
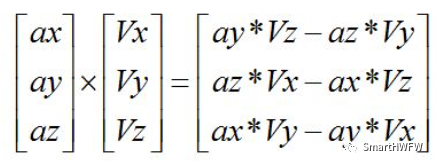
// Error is sum of cross product between estimated and measured direction of gravity halfex = (ay * halfvz - az * halfvy); halfey = (az * halfvx - ax * halfvz); halfez = (ax * halfvy - ay * halfvx);
4.消除误差, (通过对重力分量叉乘后的误差进行积分,可以得到角速度值。ki为积分系数,dt为积分周期)
integralFBx += twoKi * halfex * (1.0f / sampleFreq); // integral error scaled by Ki integralFBy += twoKi * halfey * (1.0f / sampleFreq); integralFBz += twoKi * halfez * (1.0f / sampleFreq); gx += integralFBx; // apply integral feedback gy += integralFBy; gz += integralFBz;
5.互补滤波(在PID控制器中加入误差值,并将其与陀螺仪测得的角速度相加,得到修正的角速度值。使用修正的角速度值来更新四元素,以获得更准确的姿态角信息)
// Apply proportional feedback gx += twoKp * halfex; gy += twoKp * halfey; gz += twoKp * halfez; //Integrate rate of change of quaternion gx *= (0.5f * (1.0f / sampleFreq)); // pre-multiply common factors gy *= (0.5f * (1.0f / sampleFreq)); gz *= (0.5f * (1.0f / sampleFreq));
6.求解微分方程
qa = q0; qb = q1; qc = q2; q0 += (-qb * gx - qc * gy - q3 * gz); q1 += (qa * gx + qc * gz - q3 * gy); q2 += (qa * gy - qb * gz + q3 * gx); q3 += (qa * gz + qb * gy - qc * gx);
7.四元数归一化
// Normalise quaternion recipNorm = invSqrt(q0 * q0 + q1 * q1 + q2 * q2 + q3 * q3); q0 *= recipNorm; q1 *= recipNorm; q2 *= recipNorm; q3 *= recipNorm;
8.四元数求解欧拉角 (在求解角度时要清楚的知道导航坐标系是:东北天; 北东地)
roll = asinf(2 * q0 * q2 - 2 * q1 * q3) * (180 / M_PI); // 绕X轴旋转 pitch = atan2f(2 * q2 * q3 + 2 * q0 * q1, -2 * q1 * q1 - 2 * q2 * q2 + 1) * (180 / M_PI); // 绕Y轴旋转 yaw = atan2f(2 * q1 * q2 + 2 * q0 * q3, -2 * q2 * q2 - 2 * q3 * q3 + 1) * (180 / M_PI); // 绕Z轴旋转
3.算法效果演示
不足:
1)当X轴角度大于90度时,Y轴角度发生了漂移
2)在从旋转到静止的过程之后,Z轴角度没有趋近于0度。
责任编辑:彭菁
-
滤波器
+关注
关注
161文章
7811浏览量
178075 -
导航
+关注
关注
7文章
528浏览量
42411 -
惯性传感器
+关注
关注
2文章
169浏览量
27946
原文标题:MEMS_惯性传感器14 - Mahony 滤波算法的代码分析
文章出处:【微信号:SmartHWFW,微信公众号:SmartHWFW】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
求Sigmadsp的高阶滤波器计算公式
抗EMI滤波器设计与应用原理
LC低通滤波器的截止频率是怎么推导出来的?公式是什么?

一阶数字低通滤波器原理及公式推导
如何理解卡尔曼滤波器?卡尔曼滤波器状态方程及测量方程
低通滤波器截止频率计算公式_作用和用途
模拟无源滤波器设计(九)-Gaussian滤波器设计详解
在连续时间域中比较Papoulis滤波器和Chebyshev滤波器





 Mahony滤波器的原理和公式推导
Mahony滤波器的原理和公式推导










评论