麦克斯韦的方程式

詹姆斯·克拉克·麦克斯韦是一位苏格兰物理学家，他最著名的是他在经典电磁学物理理论方面的工作。我们经常谈论麦克斯韦方程组，它巧妙地将所有电磁现象打包成四个非常简单的方程式。

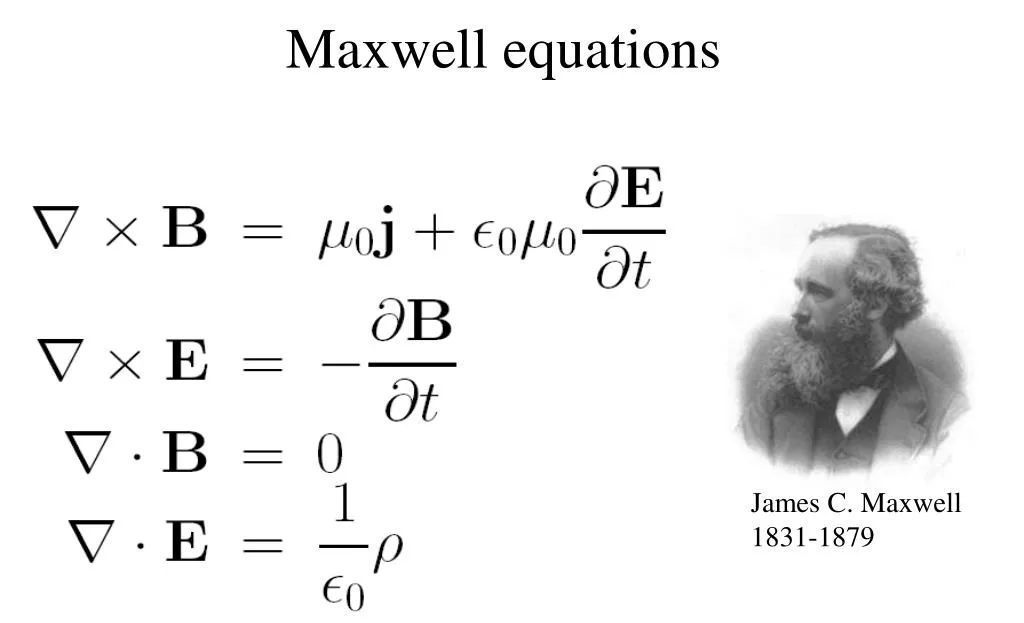
除此之外，麦克斯韦还从事电磁学以外的物理学其他领域的研究。事实上，他为我们理解热力学、热能传递研究做出了巨大贡献，以至于他在这个领域还有很多以他的名字命名的关系式。

上图就是其中一个例子，它看起来很复杂，但我将在本文中逐步解读它的含义。我们将从热力学第一定律开始，它基本上是一个关注能量守恒的定律。让我们考虑一个特定的系统来研究。

假设我们正在研究一种由许多小原子组成的气体，并且假设这种气体是孤立的。现在我们可以说这种气体具有一定的“内能”，并用字母U标记。事实上，内能基本上是所有这些小原子的能量总和，包括它们的动能以及由于它们相互施加的力而产生的势能。

现在，这种气体有多少内能并不是特别重要，重要的是内能如何变化。我们可以为内能的变化写一个简单的表达式，我们称之为dU。在这个简单的系统中，内部能量可以以两种方式变化：一种是热量的传递，另一种是系统做功，可以用公式写成dU=δQ-δW。

有必要澄清一下为什么这里有一个减号，这与我们如何定义能量流有关。在这里，热量被转移到气体中，δQ为正，反之为负；而当系统对外做功时，δW为正，反之为负。这是最初从事这项工作的科学家选择的约定。

现在，我们还可以更详细地了解热量和功。我们可以根据系统的其他属性来描述它们，比如它的温度、压力、体积和熵。具体来说，由于热量传递引起的能量变化可以通过系统的温度乘以其熵的改变来描述：δQ=TdS。由于系统所做的功而转移的能量由系统压力乘以其体积变化得出：δW=PdV。因此，我们可以将整个式子重新写成以下形式：dU=TdS-PdV。

接下来，我们将用到一个数学规则。每当我们有一个看起来像这样的表达式时：dz =Adx+Bdy，我们可以使用微积分的知识得到A和B的表达式。

我们现在可以采用这个表达式，并回到我们热力学第一定律的表达式。我们意识到，如果体积保持不变，温度必须等于内能相对于熵的变化率；同样，如果熵保持不变，压力必须等于内能相对于体积的变化率。

我们可以更进一步，考虑采用二阶导数。

现在，从数学上来看，这两个量是相等的。这意味着当我们熵保持不变，改变体积时温度变化的速度，等于体积保持不变时压力随熵改变的速度： 。在这里我们发现了温度如何随体积变化以及压力如何随熵变化之间的全新关系。这是我们应用数学和热力学定律发现的，如果仅从系统的物理特性来看并不明显。

这里的这个方程是麦克斯韦关系式的一个例子。在不同的情况下，还有更多基于热力学的公式。它们的定义可用于推导其他麦克斯韦关系，如下所示。

所以基本上，麦克斯韦在许多领域做了很多重要的工作，因此他的电磁方程并不是唯一的“麦克斯韦方程”。