在统计建模领域,理解总体趋势的同时解释群体差异的一个强大方法是分层(或多层)建模。这种方法允许参数随组而变化,并捕获组内和组间的变化。在时间序列数据中,这些特定于组的参数可以表示不同组随时间的不同模式。
今天,我们将深入探讨如何使用PyMC(用于概率编程的Python库)构建分层时间序列模型。
让我们从为多个组生成一些人工时间序列数据开始,每个组都有自己的截距和斜率。
import numpy as np
import matplotlib.pyplot as plt
import pymc as pm
# Simulating some data
np.random.seed(0)
n_groups = 3 # number of groups
n_data_points = 100 # number of data points per group
x = np.tile(np.linspace(0, 10, n_data_points), n_groups)
group_indicator = np.repeat(np.arange(n_groups), n_data_points)
slope_true = np.random.normal(0, 1, size=n_groups)
intercept_true = np.random.normal(2, 1, size=n_groups)
y = slope_true[group_indicator]*x + intercept_true[group_indicator] + np.random.normal(0, 1, size=n_groups*n_data_points)
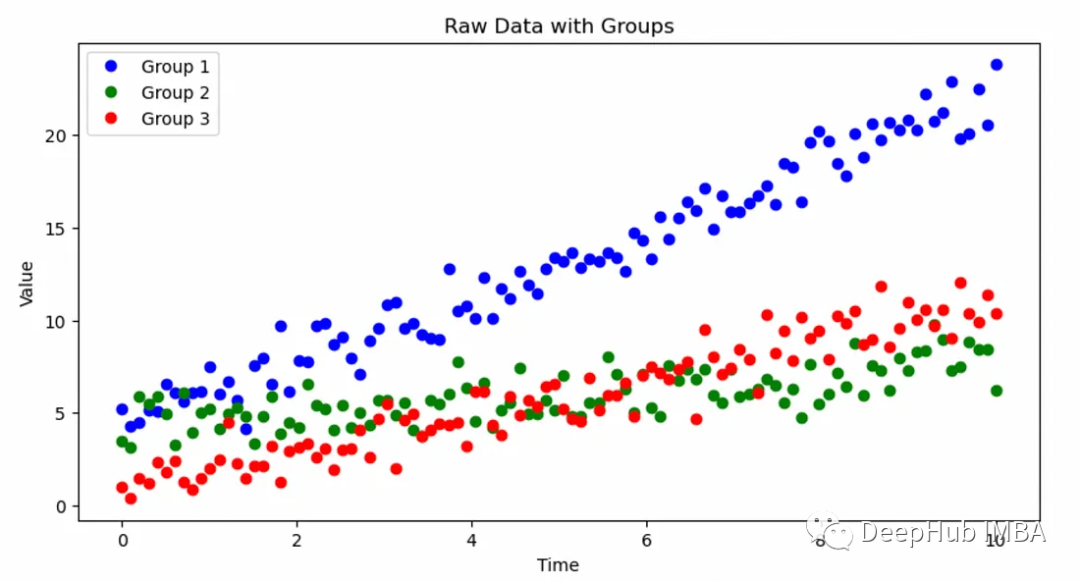
我们生成了三个不同组的时间序列数据。每组都有自己的时间趋势,由唯一的截距和斜率定义。
colors = ['b', 'g', 'r'] # Define different colors for each group
plt.figure(figsize=(10, 5))
# Plot raw data for each group
for i in range(n_groups):
plt.plot(x[group_indicator == i], y[group_indicator == i], 'o', color=colors[i], label=f'Group {i+1}')
plt.title('Raw Data with Groups')
plt.xlabel('Time')
plt.ylabel('Value')
plt.legend()
plt.show()
下一步是构建层次模型。我们的模型将具有组特定的截距(alpha)和斜率(beta)。截距和斜率是从具有超参数mu_alpha、sigma_alpha、mu_beta和sigma_beta的正态分布中绘制的。这些超参数分别表示截距和斜率的组水平均值和标准差。
with pm.Model() as hierarchical_model:
# Hyperpriors
mu_alpha = pm.Normal('mu_alpha', mu=0, sigma=10)
sigma_alpha = pm.HalfNormal('sigma_alpha', sigma=10)
mu_beta = pm.Normal('mu_beta', mu=0, sigma=10)
sigma_beta = pm.HalfNormal('sigma_beta', sigma=10)
# Priors
alpha = pm.Normal('alpha', mu=mu_alpha, sigma=sigma_alpha, shape=n_groups) # group-specific intercepts
beta = pm.Normal('beta', mu=mu_beta, sigma=sigma_beta, shape=n_groups) # group-specific slopes
sigma = pm.HalfNormal('sigma', sigma=1)
# Expected value
mu = alpha[group_indicator] + beta[group_indicator] * x
# Likelihood
y_obs = pm.Normal('y_obs', mu=mu, sigma=sigma, observed=y)
# Sampling
trace = pm.sample(2000, tune=1000)
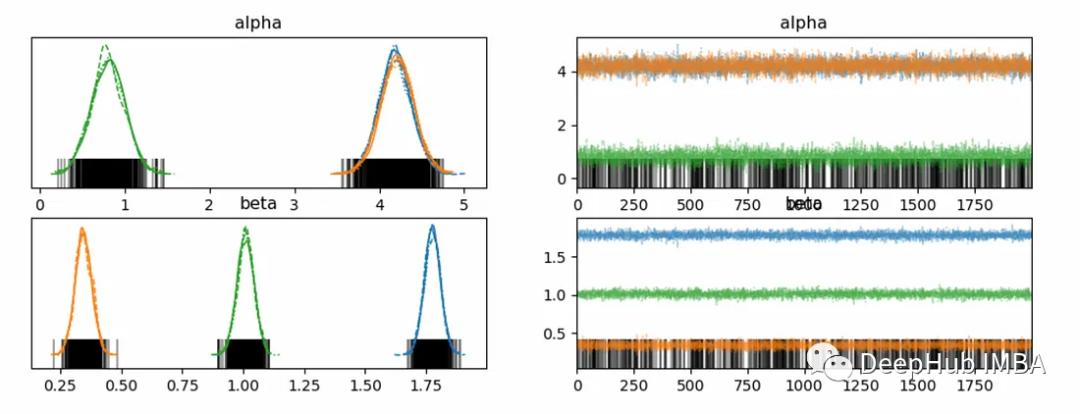
现在我们已经定义了模型并对其进行了采样。让我们检查不同参数的模型估计:
# Checking the trace
pm.plot_trace(trace,var_names=['alpha','beta'])
plt.show()
最后一步是将原始数据和模型预测可视化:
# Posterior samples
alpha_samples = trace.posterior['alpha'].values
beta_samples = trace.posterior['beta'].values
# New x values for predictions
x_new = np.linspace(0, 10, 200)
plt.figure(figsize=(10, 5))
# Plot raw data and predictions for each group
for i in range(n_groups):
# Plot raw data
plt.plot(x[group_indicator == i], y[group_indicator == i], 'o', color=colors[i], label=f'Group {i+1} observed')
x_new = x[group_indicator == i]
# Generate and plot predictions
alpha = trace.posterior.sel(alpha_dim_0=i,beta_dim_0=i)['alpha'].values
beta = trace.posterior.sel(alpha_dim_0=i,beta_dim_0=i)['beta'].values
y_hat = alpha[..., None] + beta[..., None] * x_new[None,:]
y_hat_mean = y_hat.mean(axis=(0, 1))
y_hat_std = y_hat.std(axis=(0, 1))
plt.plot(x_new, y_hat_mean, color=colors[i], label=f'Group {i+1} predicted')
plt.fill_between(x_new, y_hat_mean - 2*y_hat_std, y_hat_mean + 2*y_hat_std, color=colors[i], alpha=0.3)
plt.title('Raw Data with Posterior Predictions by Group')
plt.xlabel('Time')
plt.ylabel('Value')
plt.legend()
plt.show()

从图中可以看出,分层时间序列模型很好地捕获了每组中的单个趋势,而阴影区域给出了预测的不确定性。
层次模型为捕获时间序列数据中的组级变化提供了一个强大的框架。它们允许我们在组之间共享统计数据,提供部分信息池和对数据结构的细微理解。使用像PyMC这样的库,实现这些模型变得相当简单,为健壮且可解释的时间序列分析铺平了道路。
-
python
+关注
关注
56文章
4811浏览量
85103 -
Alpha
+关注
关注
0文章
45浏览量
25774
发布评论请先 登录
相关推荐
【「时间序列与机器学习」阅读体验】全书概览与时间序列概述
使用PyMC3包实现贝叶斯线性回归
小波回声状态网络的时间序列预测
基于系数矩阵弧微分的时间序列相似度量
如何基于Keras和Tensorflow用LSTM进行时间序列预测
如何使用频繁模式发现进行时间序列异常检测详细方法概述
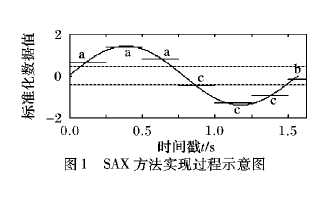
如何用Python进行时间序列分解和预测?

基于时间卷积网络的通用日志序列异常检测框架

如何使用SBC ToolBox云平台进行时间序列分析?




 使用PyMC进行时间序列分层建模
使用PyMC进行时间序列分层建模










评论