量子金融算法发布！本源开发QmRMR算法加速债务监测

2014年3月4日起，“11日超日债“成为了我国首例违约公募债，从此债券违约的案例陆续出现。因此建立债券违约预警模型对稳定经济的健康发展起着重要的作用，而选择有效的检测指标则可以提高模型的学习效率和准确率，从而加快检测速度。11日超日债（图片来源于网络）

近日，本源量子团队开发出量子mRMR算法（QmRMR），加速分析识别金融风控领域企业债务违约行为。在筛选预警模型中有效指标时，团队利用量子近似优化算法（QAOA）对全局最优指标的选取进行平方级加速，改进了最大相关最小冗余（mRMR）算法，这一方法大大减少了债务监测中的冗余分析指标，将成功降低预测债券违约模型中的过拟合风险。

01mRMR算法减少债务信息“冗余”数据降维在金融数据分析中相当重要，当数据维度过高时，高维数据的各个维度间极易存在较强的相关性，容易产生大量冗余信息。这种情况下，我们无法直观理解数据，在后续的数据挖掘、模型分析时也面临困难。冗余的信息不仅使得模型难以收敛，内存消耗大，甚至会出现过拟合的现象，直接干扰后续分析的结论。

降维的方法多种多样，经典的降维方法有主成分分析（PCA），奇异值分解（SVD)等方法。上面提到的两种常见算法的优点是通用性强，效果明显，而缺点则是线性组合的现存数据与历史数据无法并存，仅通过现存数据无法全面分析，且不具有可解释性。特别是在金融领域中，各种指标间的相关性较大，例如财务报表中形容偿债能力的指标就有流动比，速动比，长期负债比等。

而最大相关最小冗余（mRMR）算法和以上列举的算法不同，它可以直接选取和剔除指标。mRMR方法能够在样本指标与目标指标（债券是否违约的标签）之间的交互信息达到最大的同时，使得选取指标内部的平均交互信息较少。而在选取指标之前，是无法预先知道能够选取的指标个数，所以需要对mRMR模型进行改进，使得我们可以自由控制指标选取个数的同时还能够将问题转化为二次二值无约束的优化问题，也就是QUBO问题。并且我们在数学的原理证明了该改进的正确性。

02利用量子近似优化算法（QAOA）加速挖掘全局最优指标目前，原有的mRMR算法选取指标所使用的增量搜索方法往往只能得到一个局部最优结果。我们通过对算法的改进可以在无约束的情况下自由选取指标个数，在后续使用支持向量机进行债券违约效果检验时，发现改进后的QmRMR算法选取的指标能够以高概率遍历得出一样的全局最优指标选取方案。在研究中，我们使用上市公司公开的财务报表作为分析指标，来预测该公司发行的债券是否违约。我们基于偿债能力、盈利能力、现金流量、资本结构四个维度，利用改进后的量子mRMR方法，在财务报表中选取出20个样本指标（将mRMR稍作改进，就可以自由控制选取指标的个数）。之后我们使用传统的支持向量机来分类判断后续的指标选取是否有效，以及债券是否违约。在控制不同的指标个数选取的情况下，分类的结果如下图（其中各项指标都是衡量分类器的标准，越接近1说明该分类器的性能越好）。

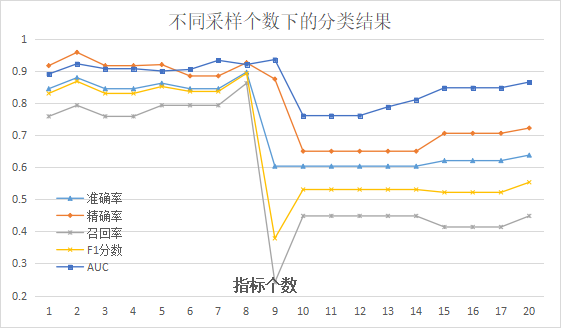
在不同样本指标个数下的分类结果：越接近1说明该分类器的性能越好上图是在不同的指标选取个数的情况下，五个衡量分类器的指标的变换情况。综合可以看出，我们在用量子mRMR选取8个最优指标时分类的效果达到最优。以该8个指标的选取过程为例，我们在实验中与使用经典方法选取指标得到的遍历结果进行对比，可以发现QAOA算法能够以较高的概率得到和经典一致的结果。下图则展示了在迭代到80层的情况下，运行量子线路得到最优选取方法的概率。可以看出，随着迭代的次数的增加，该概率总体呈现上升的趋势，并且最终可以在每次运行量子线路时都能够以超过0.3的概率得到最优解。

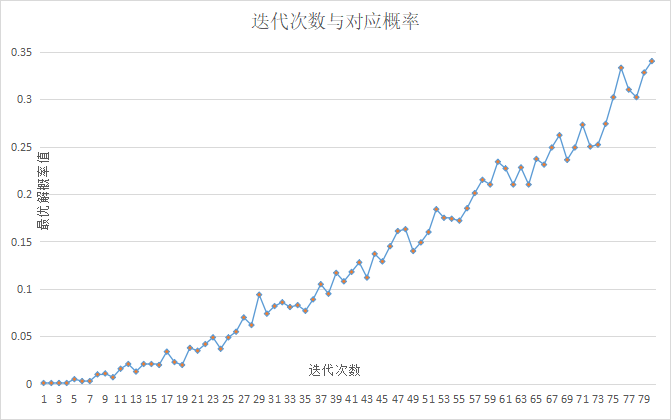
随着算法迭代次数变多，单次运行线路得到最优选取方法的概率在选取8个指标时达到较好的预测结果可以说明该8个指标和目标分类结果最大相关，且能够从不同的维度来衡量是否会出现债券违约。我们在56次的实验对比中发现，QAOA算法均能够以较高的概率得到和经典遍历一样的结果，这证明了QAOA的稳定性。相比于经典计算，本源量子团队在此次研究中开发出的QmRMR算法能够为全局优化指标选取带来二次加速，这对未来处理违约检测等场景中的大规模金融数据有着重要的意义。