仓位控制！本源量子金融在投资组合方向再获新进展

在证券投资过程中除了要考虑收益，还要考虑风险，我们通常根据风险和收益的综合衡量来决定各只证券的投资占比。在实际的组合中每一项投资都有自己的任务和价值，这时候，手头的资金应该以何种比例分配到各只证券中就尤其重要。目前普遍的量子金融算法往往解决的是投/不投的二值优化问题，无法做到仓位管理。这次本源的研发团队给出了更具落地价值的考虑投资比例的量子投资组合优化方案。

01用量子计算探索投资组合最优解

投资组合优化问题是量化金融中较为典型的一类问题。而作为现代金融投资理论的基础，Markowitz提出了均值方差（M-V）模型，其以方差表示风险，以均值来表示期望收益率，同时证券投资组合的总收益率则为各只证券的期望收益率的加权平均；在研究投资组合优化问题时，我们可以通过找寻均值方差（M-V）模型的最优函数值，进一步得到证券投资的最优投资占比。然而当投资组合优化问题规模较大以及亟待优化证券数目较多时，采用经典方法求解该问题需要消耗大量的计算资源。

为了降低计算资源的消耗，寻求速度上的提升，本源研发团队考虑了Grover适应性搜索算法（后称GAS算法）和变分量子算法（后称VQA算法）两种不同的量子解决方案。

• Grover适应性搜索算法（GAS）

由于在证券投资中，交易单位为手，同时人民币的最小单位为分，我们无法以任意精度的投资占比来进行投资，因此我们考虑采用Grover适应性搜索算法（GAS）以更贴近现实投资情形的方式来解决该问题。

• 变分量子算法（VQA）

但同时，受限于目前经典计算机可模拟的量子比特数，GAS算法目前可解决的投资组合优化问题的规模较小，因此我们考虑另一种可有效解决大规模证券的优化方法——采用拟设为hardware efficient ansatz（HEA）的变分量子算法（VQA）。02 投资组合优化：二次规划（QP）问题目前在量子金融领域，为解决投资组合优化问题，目前已有算法都会将M-V模型抽象为只考虑是否买入的二次无约束二值优化问题（QUBO），同时采用一些典型的量子优化算法如量子近似优化算法（QAOA）等对问题进行优化。我们在此之前也发布过基于这种无仓位模型进行改进后的量子应用。

这种模型使用场景限制较多，尤其在用于证券投资时，由于其决策变量仅可以为二值，其中0表示不买入该只证券，1则表示买入该只证券。而在现实中，人们在证券投资时往往不会简单地决定一只证券的买入与否，而会将手中的资金以一定的比例分配到各只证券中，此时按照何种比例分配资金使得自己的收益最大同时风险最小成了人们考虑的首要问题。不同于QUBO问题，此时的决策变量将为0，1间的小数，代表各证券的投资占比，同时所有证券的投资占比和为1。可以看到实际问题中的投资组合优化是一个典型的二次规划（QP）问题。

为解决如上的二次规划问题，本次研究中，我们除了考虑将QP问题转化为QUBO问题进而利用可以找到全局最优的GAS算法对问题进行优化。同时也考虑了在含噪中等规模量子计算(NISQ)时代的硬件条件以及现有量子芯片的拓扑结构，采用拟设为hardware efficient ansatz（HEA），对真机友好的变分量子算法对问题进行直接优化。

03量子比特数较少时，VQA量子算法仍可实现较大规模数值求解

对于GAS算法，受限于经典计算机可模拟的量子比特数，本次研究我们对4只证券进行实证分析

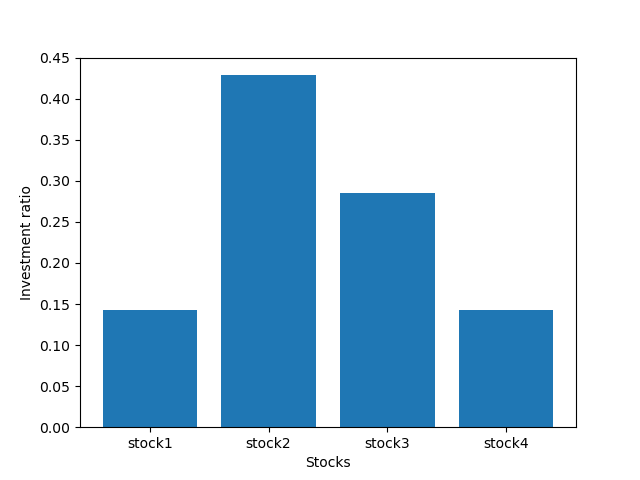
通过实验我们验证了GAS算法可以得到与经典遍历方法相同的结果，但不同于经典遍历方法，GAS算法相较于经典方法提供了近似二次加速。该次实验中，GAS算法仅通过86次查询即搜索到问题的最优结果。由此推广，随着可模拟比特数的增加，GAS算法将具有较好的应用。

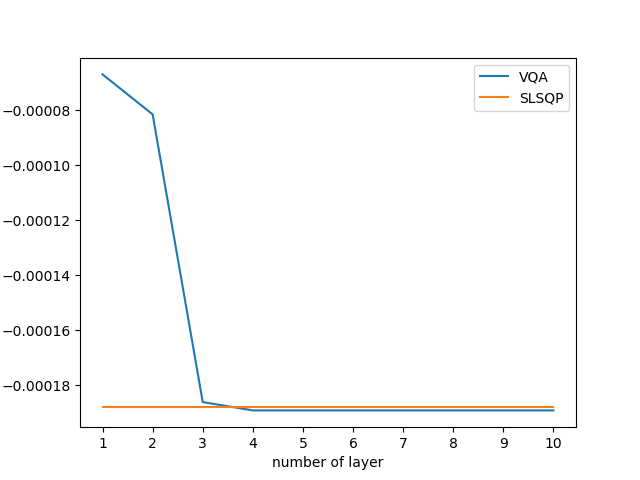
而对于采用拟设为HEA的VQA，我们对6只证券进行实证分析

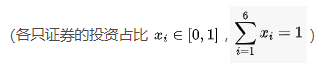
对比经典二次规划方法——序列最小二乘规划（SLSQP）算法，发现优化结果可以近似甚至优于该方法，如下所示。同时若有n只证券，该方法仅需要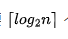个比特，如此在当下经典计算机可模拟量子比特数较少时，仍然可以实现对证券规模较大的投资组合优化问题进行优化求解。

本源量子近年来一直在量子金融领域进行相关研究与开发：联合建信金融科技推出国内首批量子金融应用——量子期权定价应用与量子VaR值计算应用，发布可用于金融衍生品收益计算的量子期权策略应用，上线可预测金融概率、进行网络监控和故障溯因新量子贝叶斯算法应用程序，开发出可快速分析识别企业债务违约行为的量子mRMR算法，发布基于GAS算法的投资组合优化应用等。随着量子技术的成熟和商业可行性的提高，量子计算将逐步展现其在金融领域的巨大技术优势和带来的经济效益。