瞬态热阻抗准确计算IGBT模块结壳热阻的方法

随着半导体技术的迅速发展以及绝缘栅双极型晶体管（insulated gate bipolar translator，IGBT）模块的普遍应用，电力电子可靠性要求不断提高，而过热失效这一主要失效原因亦成为IGBT器件研制的障碍。为解决这一瓶颈问题，近年来，国内外专家学者们也将关注的焦点放在了IGBT模块的热失效分析方面。热阻这一表征半导体器件热传导的参量也成了热失效问题中的一个热点。

IGBT热阻的测试及计算方法常见的有以下几种，包括热传导法、热敏参数法、物理接触法、红外热成像法、等效热网络模型法等。

热传导法以IGBT定义式为基础进行热阻计算。这种方法具有用直接基于尺寸参数和材料热特性解算模块结壳热阻和能清楚地反映出模块内各层构造热阻值等优点，其不足之处在于模块内各层导热材料厚度与有效导热面积近似，且忽略各层材料热导率随着温度和退化程度的变化。

热敏参数法首先得到温敏参数，由温敏参数求得IGBT的结温，再根据IGBT热阻的计算式求得其热阻。该方法优点是不易对器件造成破坏；缺点是引入了较多的测量误差，壳温最大值点难以确定，并且该方法需要在IGBT模块达到热稳态时才能进行求解。对此也有很多文献对该方法进行改进。

物理接触法主要有利用热电偶和光纤探头直接测量结温或者壳温的。这种方法具有可直接求出测量点在任意时间内的温度等优点；其不足之处在于一方面损坏了器件，而且所产生的损伤还影响了温度分布，而另一方面测量点又不一定是温度最大值的点，这些都会产生误差。

红外热成像法就是利用红外热成像系统测温的方法。它具有测量精度高、探测速度快等优点；不足之处在于费用较高。等效热网络模型法采用计算机软件编程拟合IGBT模块瞬态热阻抗曲线获得其RC热网络模型继而获得热阻。这种方法的好处在于计算速度很快；缺点在于随IGBT模块不断劣化，热网络模型中阻容参数需不断修改且工作烦琐。

根据以上分析可知，传统的热阻计算方法在准确性、测量周期或是成本上都有着些许缺陷，因此，本文根据瞬态热阻抗计算式提出了一种可以在工况条件下快速、准确计算IGBT模块结壳热阻的方法。

IGBT模块快速计算法原理

JESD51—14中定义，在t=0时刻给半导体器件施加1个恒定的热功率，那么t时刻的瞬态热阻抗可通过下式计算：

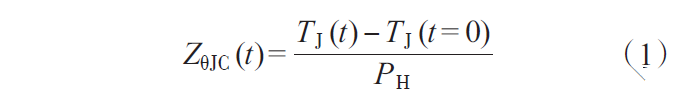
式中：

TJ(t)：为t时刻的芯片结温；

TJ(t=0)：为t=0时刻的芯片结温；

PH：为施加的热功率。

电热比拟理论认为热阻这一材料本身属性是恒定的。但热和电也有本质区别，电传得很快，也就是电场传得很快，热传得比较慢，有迟滞现象。所以以IGBT模块为例，热量从芯片上产生、往下转移的过程当中,t1时刻，热量的前端刚刚转移至衬底层（DBC）下表面，则热量流过物料的热阻就是结在DBC下表面上的热阻，根据式（1）求得的ZθJC（t1）即结到DBC底面的热阻；当t2时刻热量前端传递到铜基板底面时，那么热量所流经的热阻则为模块结壳热阻，根据式（1）求得的ZθJC（t2）即结壳热阻。所以通过研究热量前端传递到铜基板底面的时间节点及该时刻的模块结温大小，根据热量的流经热阻，由式（1）就可求得模块的结壳热阻。

为研究热量向铜基板底面传递的时间节点，对某一恒功率载荷作用下IGBT模块结壳温度0.02s之前的变化曲线进行了模拟研究，结果如图1。

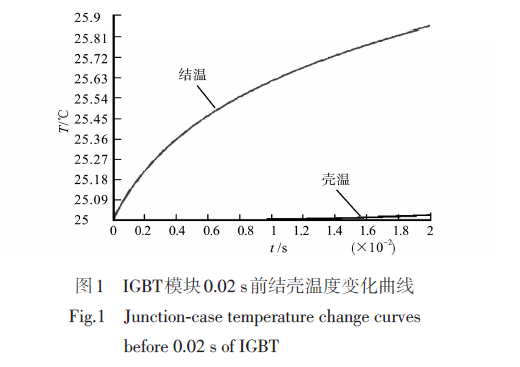
由图1可知，在t0时刻施加恒功率载荷后，芯片温度迅速上升，在0.02s时刻升高了0.85℃，而壳的温度升高出现迟滞性，在0.014s才有较为明显的升高，且温度变化速率要小于结温变化速率，在0.02s时壳温升高了0.003℃左右。为了准确研究模块热能传递过程，对图1中的壳温变化曲线进行局部放大，如图2所示。

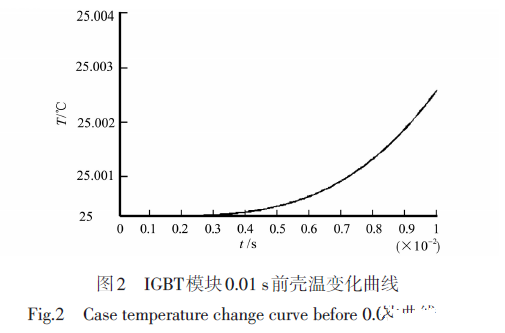
由图2可知，壳温在0.003s前不发生变化，也就是说当t=0.003s时，由芯片吸收的热量刚好传递到IGBT模块基板底面。

为了便于观察，只对模块中1组IGBT芯片的剖切面进行仿真，得出IGBT在0.003s时的瞬态纵向分布，如图3所示。

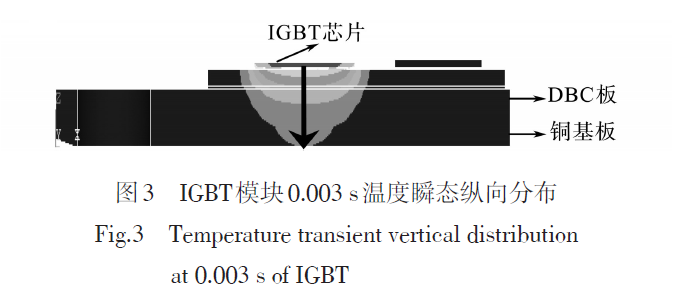
如图3所示，热流从IGBT芯片到铜基板底面是沿着箭头方向流动。基于此模拟可知0.003s下热流正好到达铜基板的底侧，这也验证了我们迟滞性理论的正确性。

通过图1～图3可知，热量从芯片传递到铜基板底面的时间为0.003s，由于IGBT模块芯片到铜基板底面的垂直距离为4.75mm，所以可以求得热量在IGBT模块中的平均传播速度为1.58m/s，远低于电子在金属导体中的传播速度，因此热量的传递与电能传递相比具有迟滞性。

IGBT快速计算模型建立

根据对式（1）的分析可知，当tp时刻热量恰好传递至模块铜基板底面时，由式（1）所计算的瞬态热阻ZθJC（tp）是模块热量所流经的热阻和，即为模块的结壳热阻。

从图1中可以看出，模块芯片向铜基板底面传热所需时间为10-3s量级，很短，所以利用这种方法可以迅速地计算出模块结壳时的热阻，不需要等IGBT模块达到稳态传热模式后再测量。故工况条件采用本方法可得到IGBT模块开机瞬间结壳热阻。因为模块在工作前各点温度与环境温度相同，所以模块结壳热阻的计算方法如下式所示：

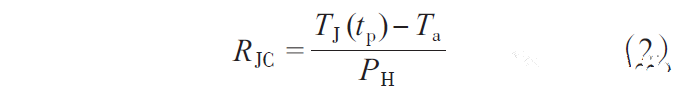
其中，tp满足：

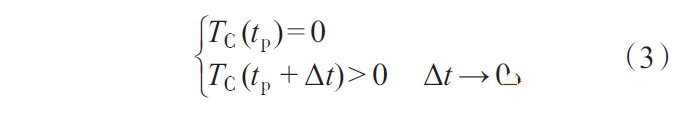
式中：

Ta：为环境温度；

Tc(t)：为t时刻模块的壳温；

Tp：为模块壳温刚开始升高的时间点。

从上述研究来看，模拟可以简便地捕捉壳温开始上升的时间点和相应时刻结温。但是在实际工况测量中，要得到这个时间节点就必须同时对模块结壳温度进行监测，并根据模块变化曲线对曲线方程进行拟合，找出ΔTc恰好不是零时的tp值。但是建立数学模型、以及求导分析过程烦琐，而且在底壳温度测量点的选择上存在随机性，从而造成结壳热阻结果存在误差。

为了可以准确获取tp时刻的结温TJ (tp)，需要对IGBT模块的传热过程进一步分析。当给IGBT模块施加一恒定功率时，热量由芯片的PN结产生并垂直向下传递，当器件的壳温没有发生变化之前，通过式（1）求得的瞬态热阻大小不受模块外部散热条件的影响，只与模块内部散热性能有关。因此，对于散热条件不同的IGBT模块，由于在此时间段，热量的传递路径完全一致，所以模块的结温变化曲线也完全一致。久而久之，因IGBT模块铜基板底部温度上升，热对流将热量散到环境中去，这时由式（1）得到的瞬态热阻较大时，会受到模块外散热的影响。针对散热条件的差异，该时刻之后IGBT模块热量传递路径发生了变化，结温曲线发生了分离。两种不同散热系数IGBT模块在加载同一热载荷下结温变化曲线如图4。

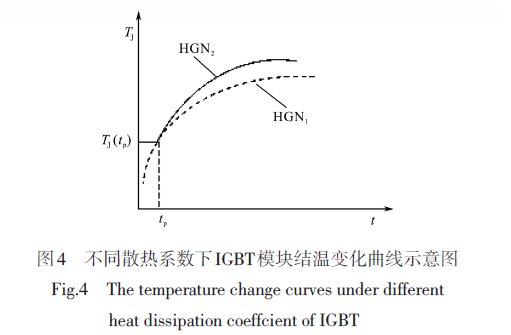
由图4分析知，在tp时刻，热量刚好由芯片传递至模块铜基板底面；在tp时刻之前两模块热量传递路径及条件完全一致，所以对于不同散热系数的IGBT模块结温在此时间段变化曲线一致；当tp时刻之后，热从铜基板底面开始散失到周围环境中，这两个模块因使用对流系数不同而改变了热传递条件，结温升高速率亦随之变化：对流系数越高的模块结温变化率越低，而对流系数越低则结温变化率越高。

IGBT模块快速计算仿真研究

为验证所提方法的准确性，采用有限元仿真进行了实例求解和计算。为了能够同时对模块热阻进行快速地计算，模拟中在同一个工作平台上建立了两个完全吻合的IGBT模块三维模型并且对其设定了不同对流系数来替代实际测量中相继两次的测量。具体解题流程如下。

1.在同一工作平台建立2个完全一致的IGBT模块3维模型，并进行完全相同的网络划分，如图5所示。

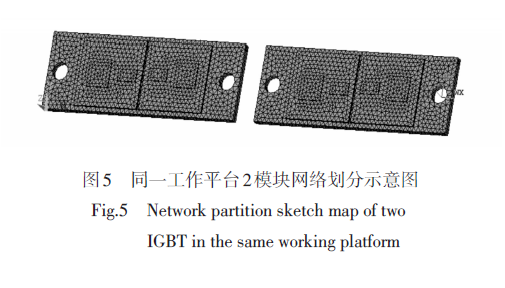
2.铜基板底面的对流系数分别设为50和100，仿真不同散热条件的模块传热特性。

3.给2个模块的IGBT芯片均施加功率为50W的热载荷。

4.通过仿真获得IGBT模块的结温变化曲线如图6所示

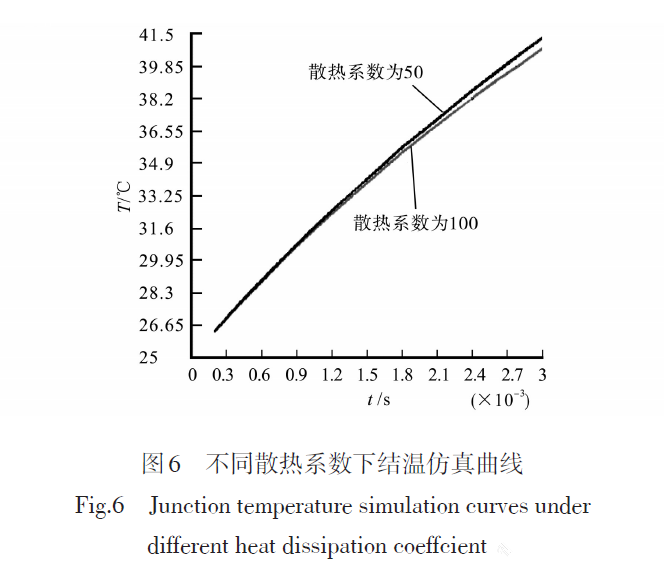
由图6可知，在t=0.0014s时，2条结温曲线发生分离，分离时的结温大小为TJ（0.0014）=33.3℃。

5.经过仿真可知，TJ（0.0014）=33.3℃，Ta=25℃，P=50W，根据式（2），求得IGBT模块的结壳热阻RJC=0.166℃/W。

为验证所提方法的准确性，采用有限元仿真进行了实例求解和计算。为了能够同时对模块热阻进行快速地计算，模拟中在同一个工作平台上建立了两个完全吻合的IGBT模块三维模型并且对其设定了不同对流系数来替代实际测量中相继两次的测量。具体解题流程如下。

解算出结壳热阻达到0.166°C·W-1。对比上述结果证明IGBT模块快速计算法是可行和正确的。

IGBT模块快速计算试验研究

1、快速计算工况条件实现方法

根据以上分析，在实际工况条件下使用该模型计算IGBT模块结壳热阻的实现方法为：

在同一坐标系下绘制不同散热条件下IGBT模块的结温变化曲线，2条曲线的分离点对应的时刻即为壳温刚开始升高的时间点tp, 此时对应的结温大小即为TJ(tp)。这样就可以根据式（2）直接计算模块的结壳热阻。

在工况条件下通过该方法计算模块结壳热阻的具体步骤如下：

1.使IGBT模块在环境温度Ta下达到热稳态，即模块各节点温度均为Ta，没有热传递发生；

2.给IGBT模块施加一恒定功率P，采集其结温变化曲线；

3.改变IGBT模块散热条件例如：组装散热器后改变铜基板和散热器间导热硅脂的厚度、未组装散热器后施加或者改变风冷后空气的速度等。再施加恒定功率P并收集其结温变化曲线；

4.寻找2次采集的结温变化曲线分离点对应的结温大小TJ (tp)；

5.根据式（2）计算模块的结壳热阻。为了使得测试过程更加快捷方便，可以提前测量不同条件下结温的变化曲线，形成数据库。

这样，实际操作时只需测量1次结温变化曲线，再与数据库中同条件结温曲线进行比对即可。

2、快速计算实验条件实现方法

通过嵌入光纤传感器可实现对芯片结温的精确测量，而无需改变模块本身的传热特性，本部分将基于分离点求取结壳热阻，并在实验室工况下对模块结壳热阻进行了测量。

根据制定的在工况条件下实验该方法的具体步骤，设计实验条件下结壳热阻测试的实现方法。

1.环境温度设置。为了更好地模拟工况条件，实验过程直接在实验室环境中进行，同时记录测试时刻环境温度的大小。

2.施加恒定功率。对IGBT模块加恒定电流30A,因发生结温分离点时刻约为数ms,故对模块栅极加+15V脉冲信号，作用时间1s。经过实测和推算，这时产热功率达到了52.6W。

3.设置不同散热系数。由于2次测量需要给模块设置不同的散热系数，所以实验过程中，第1次测量时，不做任何散热处理，第2次测量时给模块进行风冷。

4.结温采样。利用温度信号解调器能够对光纤探头收集到的光信号进行处理并发送至PC机,PC机能够对其进行曲线拟合和其他处理。在实验中，结温采样频率由计算机设定为9600Hz,也就是说温度值每s可采集9600个，每0.1ms取样一次。实测IGBT模块在加载过程中的环境温度Ta等于19.8°C。

3、 快速计算实验条件结果及分析

严格按照以上实验室条件进行测试，2次实验采集的结温点如图7所示。

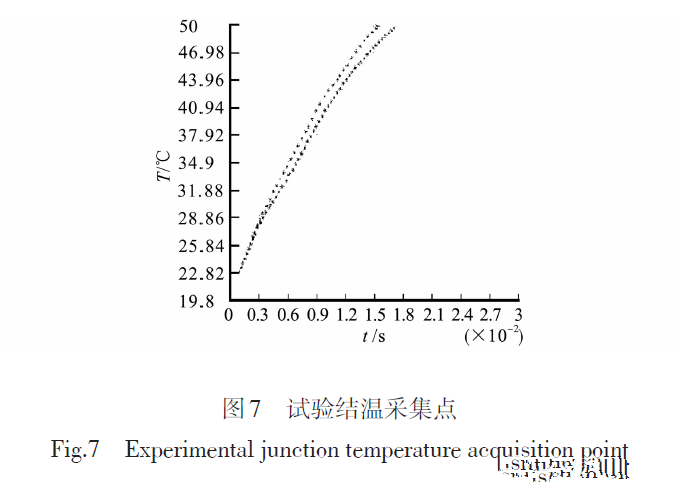
由图7及采集点数据分析可知，2次测量结温分离点时刻结温为TJ(tp)=28.6℃。根据实验条件可知，Ta=19.8℃，P=52.6W，根据式（2）求得模块的结壳热阻为RJC=0.1673℃/W。

经比对试验计算结果表明：采用结温分离点法进行模块结壳热阻的计算具有更高的准确度。同时实验过程所需要的时间较少，不需要等模块达到热稳态就可以达到快速测量的目的。

通过分析试验过程，总结发现在工况条件下使用该方法也存在一些不足：

1.工况条件下的IGBT模块都有封装结构，无法直接测量芯片结温；

2.该测试方法需要在不同对流系数下进行2次测量，第1次结束后需等待IGBT模块冷却到环境温度才可进行下一次测量；

3.工况下IGBT模块均用于组装散热器，拆下散热器或者更改散热器和铜底板之间导热硅脂厚度时工作较为烦琐且影响IGBT模块正常运行。

通过本文的分析可知，该IGBT模块结壳温度快速计算法具有以下优点：

1.无需测量模块的壳温，消除了测量IGBT 壳温时因选取节点的随机性而引入的计算误差；

2.测量误差较小；IGBT模块芯片各部分温度分布相差不大，因此测量点选择的随机性在计算热阻时几乎没有影响，环境温度及所加恒定功率均能在工况条件下测得精确；

3.测量周期短，由于热量由模块芯片向铜基板底面转移的时间为10-3s量级，所以对IGBT模块恒功率P施加所需的时间很短，收集一条结温变化曲线只需几个s即可完成。

结论

该文为寻求一种热阻快速计算新方法，给出一种通过得到不同散热情况下结温变化曲线上分离点的IGBT模块结壳热阻解算方法。设计了一种在工况条件下用此方法解决IGBT模块结壳热阻问题的实施方法及具体试验步骤，最后给出了仿真分析和试验分析的结果，采用这种方法都能迅速，精确地得到IGBT模块结壳热阻。

总结知该方法具有计算误差小、测量周期短的优点，可以实现准确、快速测量模块结壳热阻的要求。