50个关键词，带你全面了解量子计算

量子计算是一种基于量子效应的新型计算方式，它是以量子比特作为信息编码和存储的基本单元，通过大量量子比特的受控演化来完成计算任务。以量子计算为基础的信息处理技术的发展有望引发新的技术革命，为大数据和机器学习、人工智能、化学反应计算、材料设计、药物合成等许多领域的研究，提供前所未有的强力手段，对未来社会的科技、经济、金融，以及国防安全等产生革命性的影响。

本文以词条形式主要介绍量子计算相关的术语，让你对量子计算有个快速简单的总览。

量子计算的理论依据

---

叠加态Superposition叠加态原理，是量子力学中的一个基本原理，它广泛应用于量子力学各个方面，“薛定谔的猫”就是用来描述叠加态的经典比喻。在经典物理中，粒子任何时刻的状态都是空间中一个固定的点。在量子力学中，粒子可以不处于一个固定的状态（上或下），而是同时处于两种状态的叠加（上和下）。

---

量子纠缠

QuantumEntanglement

量子纠缠，它描述了粒子量子态之间的高度关联，这样的“关联”可以是多种形式，比如自旋态总是相反，或总是相同，或者是既可能相反也可能相同，但相反的可能性比相同大。只要两个粒子相互关联构成叠加态，它们就会“互相纠缠”在一起，即使在两个粒子分开到很远很远距离的情况下，它们能瞬间互相影响的“纠缠”照样存在。这种关联是经典粒子对没有的，是仅发生于量子系统中的独特现象。

---

量子测量

Measurement

量子测量是观察量子态的行为，这种观察将产生一些经典信息，该测量过程将改变量子态。例如状态处于叠加状态，则测量会将其“折叠”为经典状态（0或1），坍缩过程是随机发生的。在进行测量之前，无法知道结果如何，但是可以计算每个结果的概率，这个概率是对量子状态的一种预测，可以通过多次准备状态，对其进行测量然后计算每个结果的概率来测试该预测。

---

量子隧穿

Quantum Tunneling

量子隧穿是一种量子力学效应，指的是像电子等微观粒子能够穿入或穿越位势垒的量子行为，尽管位势垒的高度大于粒子的总能量。在经典力学里，这是不可能发生的，但使用量子力学理论却可以给出合理解释。在量子力学中，波函数表示粒子在特定位置的概率，这表明粒子存在位于障碍物另一侧的概率。

---

贝尔不等式

Bell’s Inequality最初的贝尔不等式是由爱尔兰物理学家约翰·斯图尔特·贝尔发现的，其他不等式现象后来被其他研究人员发现，贝尔的所有不等式加在一起便构成了贝尔定理。

贝尔证明了该术语的经典定义中的世界不符合当地的现实主义。“本地”意味着对象只能受到其周围环境的影响。从物理学的意义上讲，“现实主义”是指物体的性质在某人测量（甚至被测量）之前和之后都存在于人的思想之外。

经典力学说，在测量之前和之后，粒子具有真实的（确定的）值，取两个相撞并相距很远的粒子，一个人对另一个人的任何影响都必须立即通过“场”传达出来（但绝不能比光速快）。

贝尔不等式是涉及光子自旋的理论实验中的一系列测量，通过方向不同的检测器进行测量。不平等是指这样一个事实，即如果世界表现出局部真实性，则一组光子测量结果将大于另一组。然而事实并非如此，这意味着物理世界受量子力学理论支配，量子纠缠的启示仅证实了这一观点。

---

不可克隆性

No-Cloning Theorem

由于量子力学的态叠加原理和系统态的演化遵从幺正变换，使得任何量子体系的任意未知量子态无法被完全复制。即无法在不破坏原来未知态的情况下对之

---

玻色-爱因斯坦凝聚态

Bose-Einstein Condensate

玻色-爱因斯坦凝聚态是超冷原子云，华盛顿州立大学的研究员彼得·恩格斯（Peter Engels）解释说：“这一大原子团的行为不像桶中的一堆球。它的行为就像一个大的超级原子。因此，它放大了量子力学的作用。”从理论上讲，玻色-爱因斯坦凝聚物（BEC）可以充当稳定的量子比特。

---

布洛赫球

Bloch Sphere

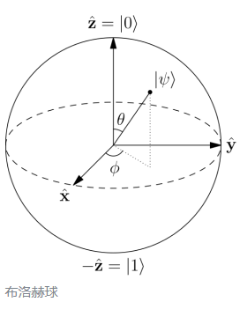
在量子力学中，布洛赫球是二级量子力学系统（量子比特）的纯态空间的几何表示，以物理学家Felix Bloch命名。布洛赫球是一个单位球，其对映点对应于一对相互正交的状态向量。布洛赫球提供了以下解释：极点代表经典位，我们使用符号|0⟩和|1⟩。然而，尽管这些是经典位表示的唯一可能状态，但量子比特覆盖了整个球体。因此，量子比特中包含了更多的信息，布洛赫球对此进行了描述。当量子比特被测量时，它坍塌到两个极点之一。这两个极点中的哪一个取决于布洛赫表示中的箭头指向哪个方向：如果箭头更靠近北极，则更有可能塌陷到北极；南极也一样。应当注意，这将概率的概念引入了布洛赫球体：箭头与垂直轴的角度θ对应于该概率。如果箭头指向赤道，则任一极都可能塌陷50-50。

---

马约拉纳费米子

Majorana Fermions形成物质的基本粒子（“费米子”）由保罗·狄拉克（Paul Dirac）于1928年提出的方程式Dirac方程来描述，这意味着宇宙中的每个基本粒子都有一个反粒子，其质量相同但电荷相反。1932年发现了第一个反粒子，与电子结合的正电子。电子和其他基本粒子具有不同的反粒子，它们通过希格斯机制获得质量，在物理学中，它们被称为“狄拉克费米子”。

1937年，意大利物理学家埃托尔·马若拉纳（Ettore Majorana）发现了一个更通用的方程式（Majorana Equation），该方程式预测了中性费米子的存在（不带电荷）是它们自己的反粒子。Majorana费米子是特殊的粒子，因为它们不是通过希格斯机制获得质量而是与其自身相互作用而获得质量，因此它们是自己的反粒子。

---

自旋

Spin自旋有时称为“核自旋”或“本征自旋”，这是基本粒子、复合粒子（强子）和原子核所携带的角动量的量子形式。旋转与实际旋转无关，物理学家使用“自旋”或“内在自旋”一词来区分粒子“有点”具有的角动量和物理旋转物体的规则角动量。

量子算法

---

量子算法

Quantum Algorithm

算法是指令的集合，允许计算函数，例如数字的平方。一个量子算法允许指令进行叠加，并创建纠缠，这使得量子算法可以完成某些常规算法无法完成的事情。

---

大数因子分解的Shor量子算法

Shor's quantum algorithm for large number factorization

1994年，贝尔实验室计算机科学家SHORP发表了一种快速进行因数分解的方法，算法利用量子计算的并行性，对任意大的整数快速做因数分解，大大降低了当前普遍使用的RSA公开密钥加密技术的破解时间。Shor算法包含两个部分：一个以传统的电脑运作的简化算法，将因子分解简化成搜寻目的问题，使用辗转相除法计算gcd(a，N)；一个量子算法，解决搜寻目的问题。

---

Grover算法

Grover Algorithm

1996年，贝尔实验室的Grover提出一种通用的搜索破译算法，其计算复杂度为O()．对于密码破译来说，这一算法的作用相当于把密码的密钥长度减少到原来的一半。Grover算法已经对现有密码构成很大的威胁，但是并未构成本质的威胁，因为只要把密钥加长1倍就可以了。

---

量子随机游走Quantum Random Walk

随机游走以及马氏链是一种非常强大的经典算法设计技术，被广泛的应用到搜索问题、采样问题以及近似估计。同样地，量子随机游走也为量子算法设计提供了一种一般化的框架。与经典的随机游走不同，给定了一个图结构，量子随机游走算法按照量子的机制(酉变换)在图结构上模拟粒子的行为。相比于经典随机游走，量子随机游走一般具有更快的首达时间。对于一些特殊的图，量子随机游走的首达时间可以比经典随机游走的首达时间指数量级的小。另外量子随机游走有着更快的混合时间。

---

求解线性方程组的量子算法

Quantum Algorithm for linear systems of equations

解线性方程组是一个基本的数学问题，在工程等领域有着重要应用。2008年Harrow等提出了一种可以在对数时间内求解线性方程组的量子算法(HHL算法)。学者们已经将HHL算法推广到机器学习领域，另外HHL算法还可应用于有限元方法，2013年Clader等提出了一种利用HHL算法解决电磁散射问题的有限元方法。

---

绝热优化算法Adiabatic Quantum Optimization

绝热优化是指采用绝热计算的方法来求解最大约束满足问题。Farhi等提出了使用绝热计算来求解最大约束满足问题的算法:系统先制备一个简单的Hamilton量并使其处于基态，然后缓慢地让系统进行绝热演化，使其演化为一个复杂的Hamilton量，这个Hamilton量的基态编码了最大约束满足问题的解。如果这个演化过程进行得足够慢，那么量子绝热定理就能保证系统一直处于基态，最后的状态也一定就是优化问题的解。

量子计算的物理实现

---

DiVincenzo标准

DiVincenzo Criteria

DiVincenzo标准是构建量子计算机的必要条件，他们首先由理论物理学家David DiVincenzo在2000年提出“量子计算的物理实现”。DiVincenzo标准由实验设置必须满足5+2个条件组成，才能成功实现量子算法，例如Grover的搜索算法或Shor因式分解。实现量子通信需要两个附加条件，例如量子密钥分发中使用的条件。

1. 具有特征明确的量子比特的可扩展物理系统。

2. 将量子比特的状态初始化为简单基准状态的能力。

3. 较长的相关退相干时间。

4. 一组“通用”量子门。

5. 特定于量子比特的测量功能。

6. 交换固定和飞行量子比特的能力。

7. 在指定位置之间忠实传输飞行量子比特的能力。

---

超导量子计算

Superconducting Quantum Computation超导量子计算的核心单元是一种“超导体－绝缘体－超导体”三层结构的约瑟夫森结电子器件，其中间绝缘层的厚度不超过10nm，形成一个势垒，库珀对能够隧穿该势垒形成超导电流。

与天然的量子体系相比，超导量子电路的能级结构可通过对电路的设计进行定制，或通过外加电磁信号进行调控。而且，基于现有的集成电路工艺，约瑟夫森量子电路还具有天然量子体系无法比拟的可扩展性。这些优点使超导量子电路成为实现可扩展量子计算最有前景的物理方案之一。超导量子计算存在的主要问题是固体体系中大量不易操控的自由度给约瑟夫森量子电路带来强烈的消相干，其中最典型的消相干过程是由具有低频特性的电荷型或磁通型偏置噪声所导致的退相干。

---

离子阱量子计算

Trapped Ion Quantum Computation1995年，Cirac和Zoller首次提出在线性离子阱体系中实现量子计算，并于同年在实验室中实现了该方案。在该体系中，Qubit是束缚在线性离子阱中单个离子的两个内能级。单Qubit的幺正变换可以通过寻址激光束与单个离子的共振相互作用来完成，2个Qubit的受控幺正变换需要利用失谐的激光束先后照射两个需要相互作用的离子，借助与整体离子串的声子相互作用来完成。

离子阱方案的主要优点是阱中的超冷离子处于一个几乎与外界隔绝的空间中，由环境引起的消相干效应非常小，因此使得量子计算的并行度较高，离子阱作为实现小规模量子计算机的强力候选被广泛关注；其主要缺点是时钟速度太慢，用数目极大的激光束脉冲操作各个离子执行逻辑运算时，运算速度难以提高。

---

量子点量子计算

Quantum Dot Computation量子点量子计算使用半导体量子点中的电子自旋作为量子比特。量子点是一种有着三维量子强束缚的半导体异质结结构，其中电子的能级是分立的，类似于电子在原子中的能级结构，因此被称为“人造原子”。量子比特编码在电子的自旋态上，使用微波脉冲或者纯电学的方法进行单量子比特操控，两量子比特逻辑门可以通过半导体腔引入的相互作用或者相邻量子点之间的电偶极相互作用来实现。

量子点方案的优点则是量子位可以是嵌套在固体材料中的固态量子器件，这与经典计算机的大规模集成电路的设计相似。半导体量子点的实现方式被认为是最有可能实现大规模量子计算机的候选方案。同时，由于与当前半导体工艺的良好兼容性，半导体量子点也成为量子计算研究领域发展最快的分支之一。另一方面半导体量子点体系受周边环境的影响比较严重，控制其退相干，维持其量子相干状态遇到了更大的挑战。

---

拓扑量子计算

Topological Quantum Computation

拓扑量子计算建立在全新的计算思路之上，应用任意子的交换相位，交换过程的“编辫”程序实现量子计算的信息处理。拓扑学研究几何形象在几何元素的连续变形下保持变的性质。如果构成量子比特的元素是拓扑不变的，基于这些量子比特的运算结果也具有拓扑不变性。由此构造的量子计算对环境干扰、噪音、杂质有很大的抵抗能力。但拓扑量子计算尚停留在理论层面，实际上还未把这些理论付诸成器件化的现实。

---

核磁共振量子计算

NMR Quantum Computation核磁共振量子计算使用核的自旋态作为量子比特。根据样品的不同，它分为液体核磁共振量子计算和固体核磁共振量子计算。液体核磁共振使用溶于液体的分子上的核自旋作为量子比特通过共振频率的不同来区分量子比特。使用与核自旋共振的射频脉冲操控量子比特，核自旋之间的交换相互作用用来实现量子比特间的纠缠和两量子比特逻辑门。

由于环境相对简单，核自旋拥有较长的退相干时间。基于核磁共振的量子调控技术也是相对比较成熟的技术。基于这些优势，液体核磁共振量子计算是目前所有实验物理体系中进展最好的，并且成为了验证量子计算原理和各种模型的绝佳实验平台。

---

光量子计算

Optical Quantum Computation量子比特的光子实现在量子信息科学中扮演着重要的角色，除了在量子密码和量子通信中非常成功的应用之外，光子量子计算也是最初实现多粒子纠缠，量子态的制备，简单量子算法的物理系统之一。光子所具有的巨大的优点在于它没有退相干，并且我们可以精确的控制和操纵它。光子量子计算吸引人们的另一点是它可以与各种量子通信的应用紧密联系在一起，比如可以用它来做分布式量子计算。

量子计算机的构成

---

量子比特

Qubit在常规计算机中，信息单元用二进制的1个位来表示，它不是处于“0”态就是处于“1”态。在二进制量子计算机中，信息单元称为量子比特(qubit)，它除了处于“0”态或“1”态外，还可处于叠加态(superposedstate)。叠加态是“0”态和“1”态的任意线性叠加，它既可以是“0”态又可以是“1”态，“0”态和“1”态各以一定的概率同时存在。

简单来说，量子比特就是一个具有两个量子态的物理系统，如光子的两个偏振态、电子的两个自旋态、离子（原子）的两个能级等都可构成量子比特的两个状态。

---

Transmon

Transmon是一种超导环形量子比特，可以在极低的温度下创建，目前最多可以将其中五个链接在一起。标准的transmon可以保持大约50微秒的相干性，可以在量子电路中使用。更重要的是，相干时间是长度的两倍，transmon数组包含10到20个循环。

---

Xmon

Xmon是由加利福尼亚大学圣塔芭芭拉分校的一个团队创建的十字形量子比特。研究小组发现，通过将五个Xmon放在同一行中，他们能够创建稳定有效的量子排列，从而提供最大的稳定性和最少的误差。像大多数其他量子比特一样，必须在接近绝对零的温度下创建Xmon。

---

拓扑量子比特

Topological Qubit

量子比特非常挑剔，即便是最轻微的扰乱，它们也会“散开”，不再可用于计算。引入拓扑量子比特概念，使其更加稳定，且能提供更多固有的防错能力。根据定义，粒子的拓扑状态就是粒子可被分解、并出现在系统不同地方的状态。一旦粒子被分解，就很难被干扰，因为必须改变所有存储在不同地方的信息。

---

量子寄存器

Quantum Register

n个量子位的有序集合称为n位量子寄存器。它的态是n个量子位的态的张量积(tensor product)。n位量子寄存器可以存储2n个n位数。

---

量子逻辑门

Quantum Logical Gates

对量子位的态进行变换，可以实现某些逻辑功能。变换所起的作用相当于逻辑门所起的作用，在一定的时间间隔内实现逻辑变换的量子装置称为量子逻辑门。与传统逻辑门不同，量子逻辑门是可逆的。量子逻辑门是量子计算与量子计算机实现的基础，可用下列方法实现：

(1)量子点系统；

(2)超导约瑟夫森（Josephson）结系统；

(3)核磁共振量子系统；

(4)离子阱系统；

(5)腔量子电动力学系统等。

---

量子逻辑网

Quantum Logical Nets

量子逻辑网络由多个量子逻辑门组成，这些量子逻辑门的操作在时间上同步。

---

随机基准

Randomized Benchmarking

一种用于确定一组量子门的平均错误率的实验技术，这涉及到应用随机电路，如果门无法正常工作，将产生零影响。基准测试是评估多量子比特量子计算机性能的重要程序。

---

量子存储状态

Quantum Memory State

量子存储状态是量子位在其中维持大量状态以在量子计算中具有价值的状态。迄今为止，这些状态已被证明是非常脆弱的，因为在量子级的最小干扰就可以破坏它们。因此，大多数使用量子比特的实验都要求将粒子冷却到接近零的绝对值。

---

量子程序

Quantum Programs

量子程序的逻辑体系一般由“经典控制部分+量子数据部分”构成。量子程序的计算操作一般由以下三部分组成：

（1）一个初化操作，包括量子变量数据的初化；（2）一系列的酉变换；

（3）一个最终的测量。

---

量子计算机的组织结构

The organization of a quantum computer

量子计算机的计算过程由算法决定，不同的算法有不同的幺正变换。量子计算机的计算过程可由常规计算机控制，由于量子计算的测量结果是概率性的，需要计算和测量多次，才能得到所需结果。量子并行是量子计算机的特点，对于串行计算及迭代运算，量子计算机不具备优势。量子计算机适合于作为常规的通用计算机的高速协处理器或外围专用处理机，或专门为实现某种量子算法或模拟某种量子系统的专用计算机。

---

量子计算机的程序语言

The programming language of a quantum computer

与经典计算机类似，为便于控制并通用量子计算机，必须通过量子计算机设计语言来描述待解决问题，因此量子计算机程序设计语言将作为未来通用量子计算机上的一种重要系统软件。现有量子算法一般固化于专用量子计算设备中，如果需要改变量子算法就必须重新设计量子计算设备，实际上，这就相当于一台求解特定具体问题（不是一类特定问题）的专用计算设备。

---

量子模拟器

Quantum Simulator

量子模拟在很大程度上起源于理查德·费曼（Richard Feynman）的1982年的提议，现已发展成为科学家使用可控量子系统研究在实验上不太可行的量子现象的领域。简而言之，现在尚不存在完整的量子计算机，并且经典计算机通常无法解决量子问题，因此“量子模拟器”提供了一种吸引人的替代方法，可以深入了解例如复杂的材料特性。

---

通用量子计算机

Universal Quantum Computer量子图灵机（QTM），也是一种通用量子计算机，是用于量子计算机的效果进行建模抽象机。它提供了一个非常简单的模型，可以捕获量子计算的所有功能。任何量子算法都可以形式上表示为特定的量子图灵机。牛津大学物理学家戴维·德意志（David Deutsch）在1985年的一篇文章中首次提出了这样的图灵机，该论文提出量子门的功能可以与传统的数字计算二进制逻辑门类似。量子图灵机并不总是用于分析量子计算。量子电路是更常见的模型，这些模型在计算上是等效的。

量子计算机的分类

---

当前，量子计算机可大致分为三类：量子退火、嘈杂中型量子（NISQ）计算、容错型通用量子计算。

量子退火Quantum Annealing

绝热量子计算机中用于解决优化和采样问题的算法。它通过允许量子系统找到其最低能量状态而起作用。在数据波动的情况下，量子比特位于最低的能量峰值上。这些都将量子比特控制和降低到零，最终得到了解决方案。

---

NISQ

NISQ是“Noisy Intermediate-Scale Quantum”的缩写，它是指“嘈杂中等规模量子“。“中等规模”指的是现在可以获得的量子计算机的尺寸大小———可能大到足以执行某些高度专业化的任务 ( 如新药和新材料的设计等) ，超出了当今超级计算机的能力范围。“嘈杂”则强调对量子比特的控制还不是非常完美，这将导致小误差随时间不断积累，如果计算时间太长，就得不到正确答案。

容错量子计算Fault-tolerant Quantum Computing量子纠错码可以用来解决退相干等硬件的不完美导致的计算错误问题。在错误的分布满足某些条件的情况下，我们可以把最终计算结果出错的概率降得任意低，这被称作容错量子计算。量子纠错是有代价的，为了降低最终出错率，需要使用很多的量子比特来进行编码。进行容错量子计算的首要条件，也就是错误率低于容错阈值(亚阈值)的初始化、量子门以及读取等操作已经能够在实验中被演示。
其他

---

量子互联网Quantum Internet

荷兰QuTech的研究人员正在尝试建立世界上第一个量子互联网。量子互联网就像普通的互联网一样，但是它可以发送量子态并建立纠缠。当然，建立全面的量子互联网非常困难。因此，他们将在2020年之前建立一个小型的四节点网络。该四节点网络将作为大型网络的测试平台。该网络的四个节点将是荷兰的四个城市：代尔夫特，阿姆斯特丹，莱顿和海牙。

---

量子霸权

Quantum Supremacy

量子霸权是指量子计算拥有的超越所有经典计算机的计算能力。在物理实验上，迄今还没有任何一台量子装置在实际实验中展现出这种能力。2019年9月20日，科技巨头谷歌(Google)一份内部研究报告显示，其研发的量子计算机成功在3分20秒时间内，完成传统计算机需1万年时间处理的问题，并声称是全球首次实现“量子霸权”。

---

相干时间

CoherenceTime

相干时间是量子叠加态可以存在的时间长度。

---

保真度

Fidelity

量子保真度不是指密度矩阵中包含的空间，而是指两个量子态彼此接近程度的度量或精度，其中最简单的例子是两个量子位。通道保真度是衡量信息在通道内保留程度的一种度量，并且与量子保真度有关。

---

退相干

Decoherence

量子计算所需的量子门是幺正变换。在量子力学理论中，幺正变换描述了一个封闭系统的演化。然而，在自然界中我们还没有发现真正的封闭系统：一个物理系统总是或多或少地与外界环境存在相互作用。由于相互作用的影响，系统演化不仅由系统本身决定还取决于环境的状态。其结果是系统演化一般不再是幺正变换。有些非幺正演化会使量子系统逐渐失去相干性，也就是量子叠加态无法持续，这个过程被称为退相干。退相干会导致量子算法失去优势。

---

量子纠错

Quantum Error Correction量子计算机总是与环境相联系，这种环境会干扰系统的计算状态，从而导致信息丢失。量子纠错通过获取系统的计算状态并将其分散到纠缠态上的量子比特上来解决这一损失。这种纠缠允许外部经典观察者观察和补救干扰，而不是观察计算状态本身，这将使它发生坍缩效应。

---

绝对零度

Absolute Zero

绝对零度是理论上可能的最低温度，在该温度下粒子的运动将最小。绝度零度在开尔文刻度上为零，等于–273.15℃。为了增加稳定性，大多数量子计算系统在接近绝对零度的温度下运行。

---

掺杂金刚石

Doped Diamonds

对金刚石的量子应用集中在识别可以在碳晶格中发现的数百种不同缺陷。物理学家发现，他们可以充分利用这些缺陷来操纵量子粒子的自旋。

---

容错材料

Fault-tolerantMaterial

容错材料是一类独特的高级材料，其内部电绝缘但在表面导电。在拓扑绝缘体的表面上诱导高温超导性为创建容错量子计算的先决条件打开了大门。这些材料之一是石墨烯,石墨烯的边缘可将其转变为一种可用于量子计算机的拓扑绝缘体。

---

量子点

Quantum Dot量子点实际上是“人造原子”。它们是半导体的纳米晶体，其中可以捕获电子空穴对，纳米晶体尺寸与光的波长相当，因此就像在原子中一样，电子可以占据离散的能级，由此可以将点限制在光子晶体腔中，在此处可以用激光探测它们。