透波高导热绝缘氮化硼材料及大功率模块双面散热封装热设计

摘 要：随着半导体功率器件的使用环境和性能要求越来越高，器件散热能力要求也随之提高。器件散热问题导致的失效占了总失效的一半以上，而双面散热封装是提高器件散热能力的有效途径之一。因此，本文针对大功率模块的双面散热封装，利用有限元计算的仿真手段进行了模块整体的热设计与特性研究。首先，分析了热对流系数对模块最高温度的影响; 其次，对比分析了单双面散热以及不同形状散热片对散热的影响; 另外，对比分析不同焊料及金属厚度对散热的影响; 最后，对优化模型进行了热应力分析，从而完成模块的热设计与热管理。研究结果对双面封装的热设计具有一定参考意义。

关键词:功率器件; 双面散热; 温度; 热应力; 形变

关键词：功率器件; 双面散热; 温度; 热应力; 形变;

1引言

目前，大功率器件尤其是第三代半导体功率器件的主要问题仍然是热引起的失效问题，其70%以上的失效是由于热引起的。因此，散热也是大功率器件发展中一直研究和优化的热点。在器件封装中，由于封装材料不同，其封装材料的热膨胀系数的差异，导致器件出现不同程度的形变和热应力积累，最终导致如焊线脱离、焊料分层、塑封体开裂分层等失效问题; 另外，温度的升高也会降低器件的性能，带来电流的载荷能力和栅压影响等问题。

大功率模块的封装形式主要还是以单面封装为主，许多研究者为此做了多方面研究，推动了功率器件的发展。但是，随着对器件散热能力要求的提高，特别是第三代半导体极高的功率密度，单面散热封装有着一定的局限性。因此，双面散热封装应运而生，其散热能力将提升30% ～ 50%。Brinkfeldt等人通过计算仿真对比了一款SiC模块，相同条件下，单面封装的最高温度为141 ℃，而双面封装为119 ℃。宁圃奇等人则通过针刺型散热片来进一步提高双面散热封装的散热能力。Cova等人通过试验和仿真，极大优化了双面散热模块的散热能力，使芯片温度在80 ℃以下。陆国权等人研究了双面SiC模块应力缓冲层形状、厚度和焊层面积对模块各层材料的受力与变形的影响规律。美国弗吉利亚理工大学通过优化模块布局，研制了高温、大功率SiC结晶型场效应晶体管功率模块。美国北卡州立大学将驱动芯片集成到功率模块内部，实现了开关频率高达3． 38 MHz的SiC功率模块。美国田纳西大学和橡树林国家实验室，针对电动汽车应用，研究了集成水冷、双面散热的SiC功率模块。日本丰田公司采用双面散热封装技术，研制了高功率密度的SiC车用电机控制器。虽然许多学者对双面散热封装模块进行了一些研究，但是其研究还略显匮乏，有待全面而深入的持续研究。而在散热特性的研究上，仿真计算无疑拥有着较大的经济和时间成本优势。

本文对一款SiC双面散热封装模块，利用热仿真对模块的整体热设计进行了全面仿真分析。首先分析了热对流系数对模块最高温度的影响; 其次对比分析了单双面散热特性以及不同形状散热片对散热的影响; 另外，对比分析不同焊料及金属厚度对散热的影响; 最后，对优化模型进行了热应力分析。本文的研究结果对双面封装的热设计具有重要的参考意义。

1仿真模型

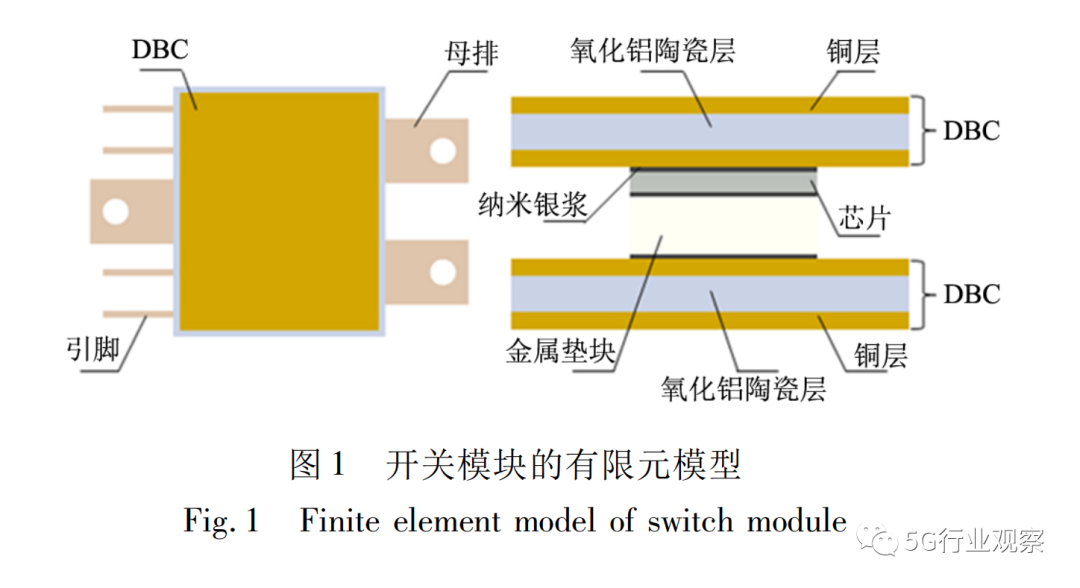
本文中，以双面散热模块为研究对象，图1为计算模型的结构示意图。如图所示，上下两层为直接覆铜陶瓷(DBC，Direct Bonding Copper) 基板，通过芯片与垫块相连，实现整体的电气互联。模型的尺寸为39 mm × 33 mm，母排尺寸为18 mm × 10 mm，引脚尺寸为16 mm × 1 mm。金属氧化物半导体场效应晶体管(MOSFET) 的芯片尺寸为:5． 46 mm × 4． 37 mm，而DBC基板陶瓷层厚度为0． 63 mm，其他部件如焊料和垫块初步尺寸为5． 46 mm × 4． 37 mm，本文将对这些参数做出优化。

有限元计算过程中，模型各部分的温度分布并不均匀，温差较大，同时形变差异也不相同。因此，对应力应变变化剧烈的焊料层、芯片、垫块和DBC基板相对应的铜层周围进行局部细化的网格划分，采用矩形映射单元，以提高计算精度。模型采用0． 2 mm的网格间距划分网格，网格总数量为622430，焊料层、芯 片、垫 块 和DBC基板相对应的铜层的网格数为172050。

当物体内的温度分布只依赖于一个空间坐标，且温度分布不随时间而变时，热量只沿温度降低的一个方向传递，称为一维定态热传导，导热现象的规律被总结为傅里叶定律［13］。此时的热传导可用式(1) 描述:

φ= －λAdt/dx (1)

式中:φ为热量;A为垂直于热流方向的截面积;dt/dx为温度t在x方向的变化率;λ为导热系数; 负号表示热传递方向指向温度降低的方向。

对流换热过程所传递的能量，可用牛顿冷却方程来计算，其数学式(2) 为:

φ=hcA(tw－tf) (2)

式中:hc为换热系数，表示单位面积温差为1 ℃时所传递的热量;A为固体壁面换热面积;tf为流体温度;tw为固体壁面温度。其中对流换热系数hc在热传导过程中尤为重要，其大小反映对流换热的强弱，物理意义是: 当流体与固体表面之间的温度差为1 K时，1 m × 1 m壁面面积在每秒所能传递的热量。

本文对应力场有限元模型计算做出以下简化:

1) 忽略自蔓延薄膜燃烧过程中可能产生的断裂和自蔓延薄膜内的纳米层的熔化流动情况，不考虑流动以及温度变化导致的自蔓延薄膜物性参数的改变;

2) 本模型主要分析焊料层应力应变的变化，不考虑焊料的流动和形状的改变，同时不考虑焊料的密度、杨氏模量和泊松比等物性参数随温度的改变;

3) 假设芯片和DBC基板互连之前平整无翘曲，不考虑硅片和基板材料的各向异性。

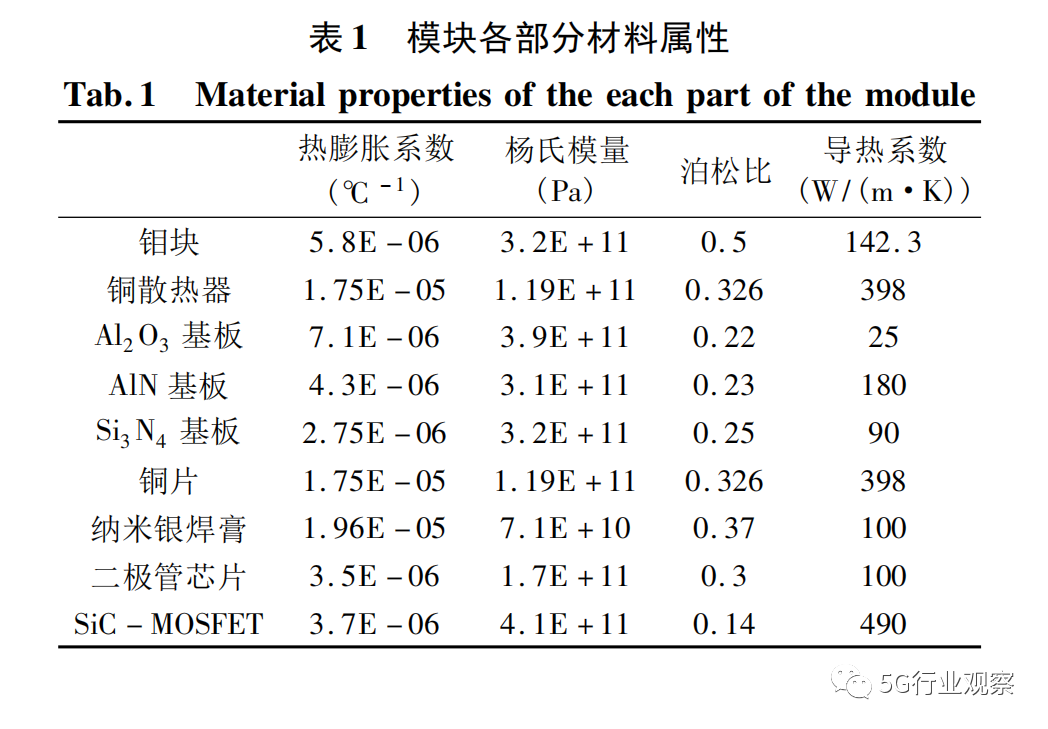
表1给出了模块各部分材料属性参数。

2结果与分析

本文中模型利用ANSYS /Workbench有限元仿真软件进行温度与热应力仿真计算，并做出以下假设:

环境温度设为22 ℃;

芯片的发热为有效热源;

器件各焊料均无空洞等缺陷且焊接良好;

散热器的散热面有效热对流系数为1000 W/(m2·K) ，其余与空气发生热量交换的等效热对流系数为5 W/(m2·K)。

2.1确定网格密度

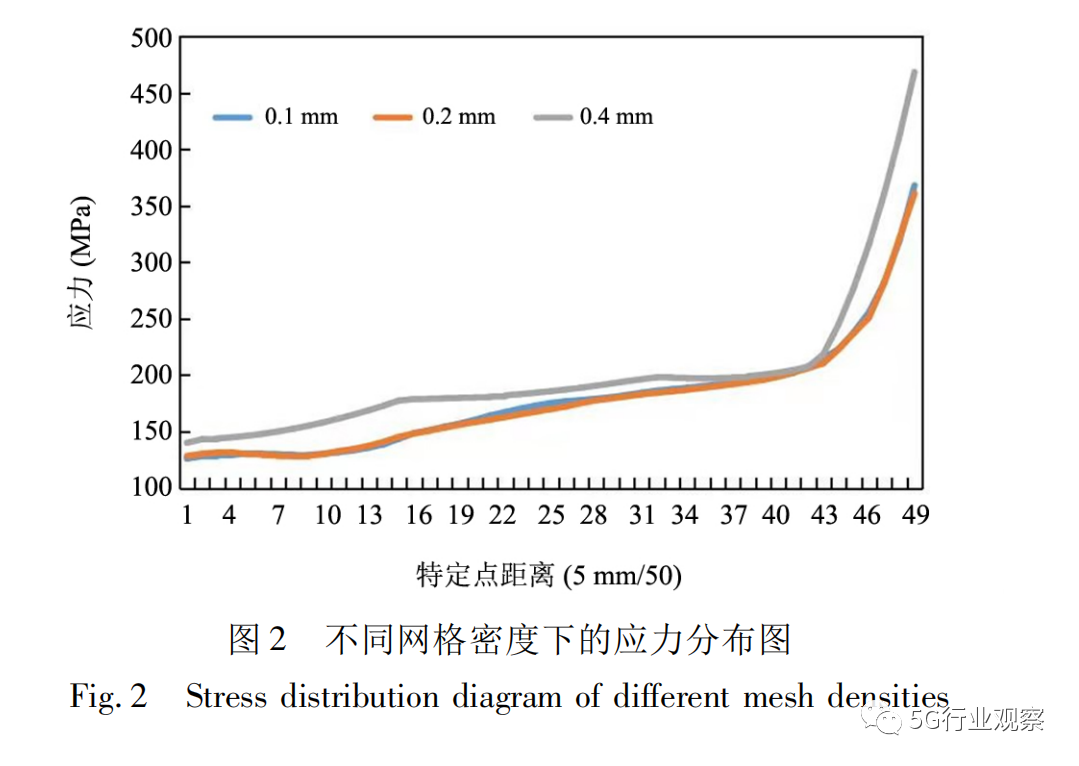
一般情况下，过大的网格密度会影响计算精度，造成结果的误差分析，而过小的网格密度则会消耗巨大的计算资源，效率低下。因此，为了提高模型的计算精度，同时节省计算资源，提高效率，本文利用“路径法”首先确定了所计算模型的网格密度，对比不同网格密度下距离特定点不同距离的应力分布，即以某一应力集中点为基准点，将基准点外5 mm距离线段划分成50段，从外往应力基准点开始对比其应力分布。如图2所示，本文分别比较了0． 1 mm、0． 2 mm和0． 4 mm的网格密度下特定点的应力分布，可以看到，0． 4 mm的应力值和0． 1 mm、0． 2 mm的应力值有较大的差别，而0． 1 mm、0． 2 mm的应力值基本相同。因此，本文采用0． 2 mm的网格密度。

2.2单双面散热对比

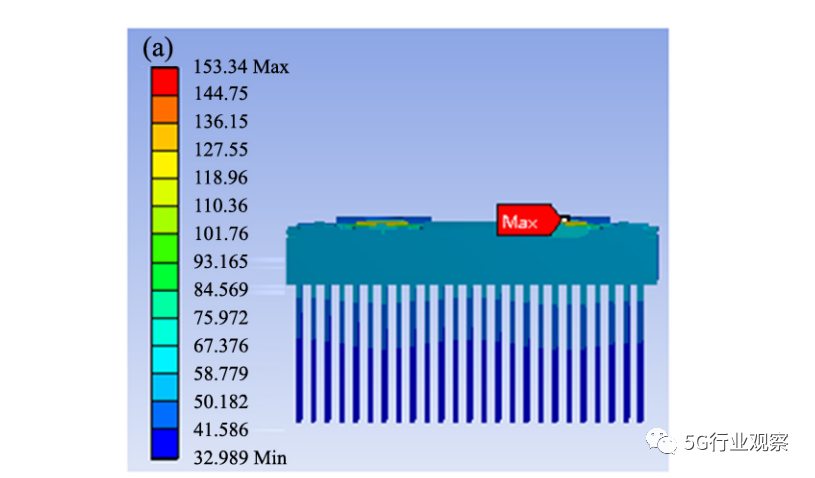
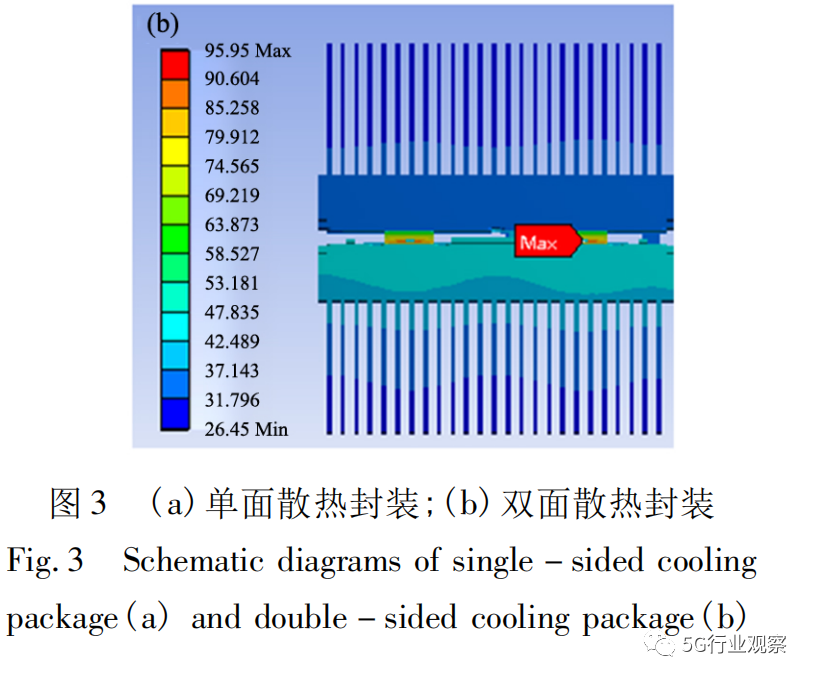
双面封装所带来最直观的优势是可以采用双面散热，其具有更多的换热面积，使单位时间内通过传热面积的热量增多，温度下降更明显。如图3所示，在热对流系数为1000 W/(m2·K) 环境下，模拟计算单、双面封装的温度场，由图可知，单面封装的最高结温为153． 34 ℃，双面封装的最高结温为95． 95 ℃，双面封装的最高结温比单面封装的最高结温减少57 ℃，散热能力提高37． 4%。双面封装所带来的优势不仅仅是热对流换热面积的增大，同时热传导面积也有增大，可以看到双面封装热传导面积的增加最直观的效果就是为器件提供了多一条竖直方向散热途径。

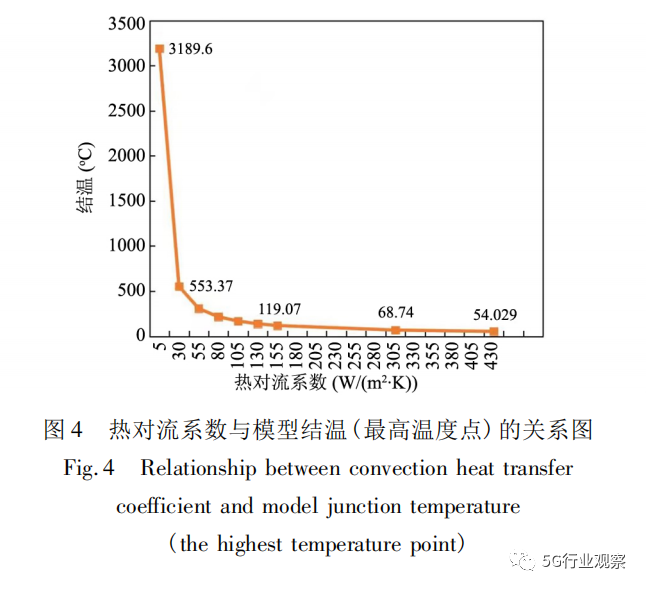
另外，本文分析了热对流系数对封装散热的影响。选用带有双面散热器模型，热对流系数与模型结温( 最高温度点) 的关系如图4所示。从图中可知，在热对流系数初始增加阶段，结温急剧下降。在对流系数150 W/(m2·K) 以上时，温度下降趋势变缓，说明热对流的增大，对温度的影响效果已经不大。因 此，在器件散热方面，除了热对流系数的影响，特别是在热对流系数影响缓慢的阶段，对其他散热影响因素的优化显得尤为重要，所以本文在下面部分对散热器、基板、焊料等进行了仿真优化。

2.3不同散热器的对比

针对市面较为常见的针式与肋片式两种散热器进行比较，基于本实验的模型与环境探讨最佳散热器效果。

2.3.1肋片式散热器

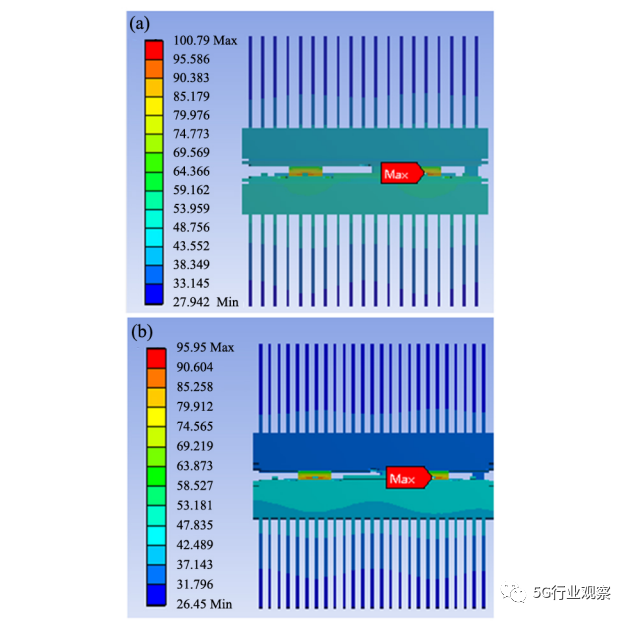
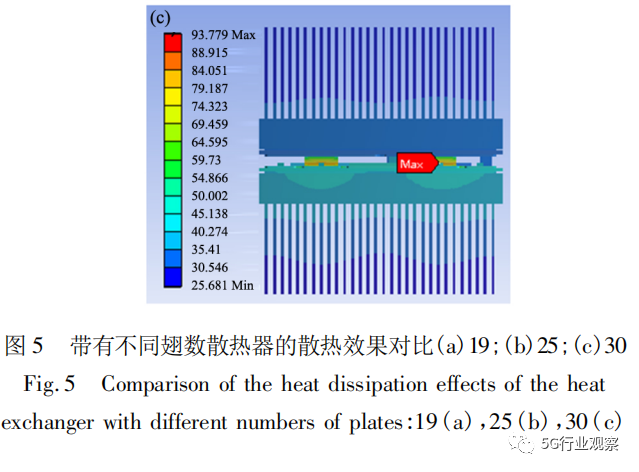
肋片式散热器具有加工相对简单的优势，肋片可以做得更薄，可通过提高散热片密度增加散热面积，从而有效地提高散热能力。因此在对比不同散热器的同时，也探究了相同厚度不同翅数的散热器对器件散热的影响。在本实验中分析了3个不同翅数的散热器，其翅数分别为19、25、30。计算结果如图5所 示，从左到右散热器翅数分别为19、25、30的散热模型，其最大结温分别为100． 38 ℃、95． 95 ℃以及93． 779 ℃，从19片的翅数增至25片时，最大结温可降低4． 41%，而从25片翅数增至30片时，最大结温仅降低2． 26%。这说明当散热器的片数密度过密时并不利于散热。

2.3.2针式散热器

针式散热器相对肋片式散热器加工较难，但在相同尺寸下针式散热器的传热面积更大，在理论上同等尺寸的针式散热器的散热效果会更佳。同样在本实验中也做出3个同直径不同针数的散热器的散热效果对比。如图6所示，从左到右散热器的pin针排数分别为19、25、30的散热模型，其最大结温分别为121． 69 ℃、108． 52 ℃以及103． 85 ℃，随着pin针数量的增加，传热面积随之增加。当散热器pin针的排数由19增加至25时，最大结温下降10． 8%。当散热器pin针的排数由25增加至30时，最高结温下降4． 3%，针式散热器与肋片式散热器具有相同的性质，当散热pin针过密时会使散热器的散热能力下降。

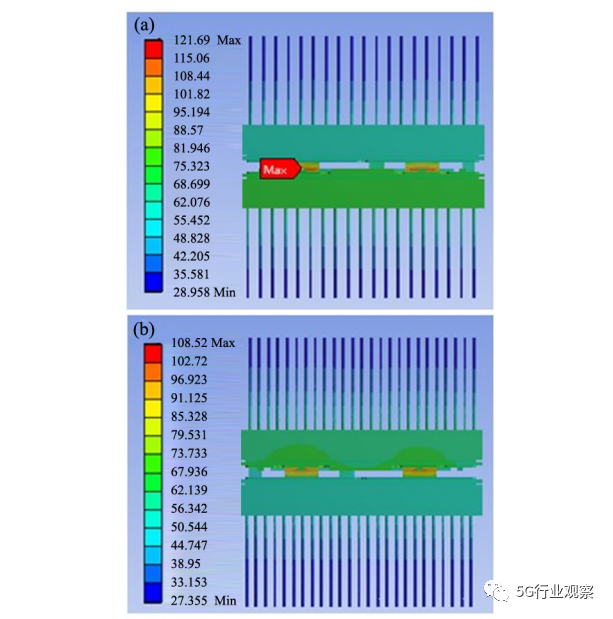
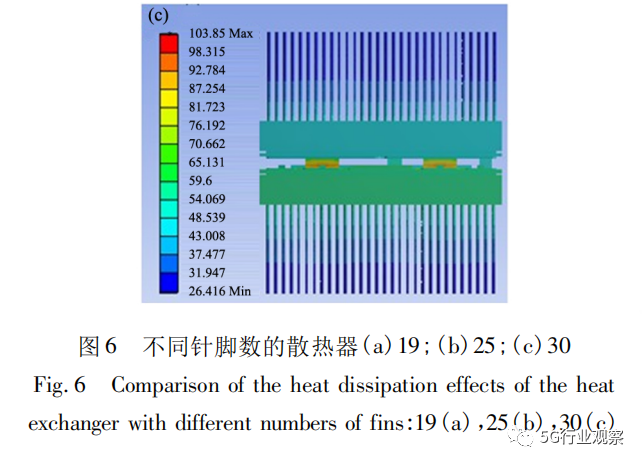
通过两种散热器结果分析对比可知( 如图5、图6) ，在同样的温度环境下，针式散热器的温度计算结果会比肋片式散热器的温度计算结果偏高，故基于本实验该模型与温度环境是用肋片式的散热器效果更佳。

2.4不同基板材料的热散热性能对比

陶瓷基板因拥有着优良的电绝缘性、高导热性以及优异的附着强度而广泛应用于电子半导体器件当中，而本实验中的器件中陶瓷基板直接与散热器连接，在整个器件当中，陶瓷基板不仅起到载流作用，同时也是散热的重要结构之一，陶瓷基板直接将芯片的热量传给散热器，减少热量经过途径，减少热阻，使器件能够及时散热。然而不同的陶瓷基板的陶瓷材料不同，其导热性能也差异较大。以下将比较市面常用的Al2O3、AlN、Si3N4这三种陶瓷基板材料性能。由 于BeO是有毒物质，在工业上无法广泛应用，所以并不对其做出比较。

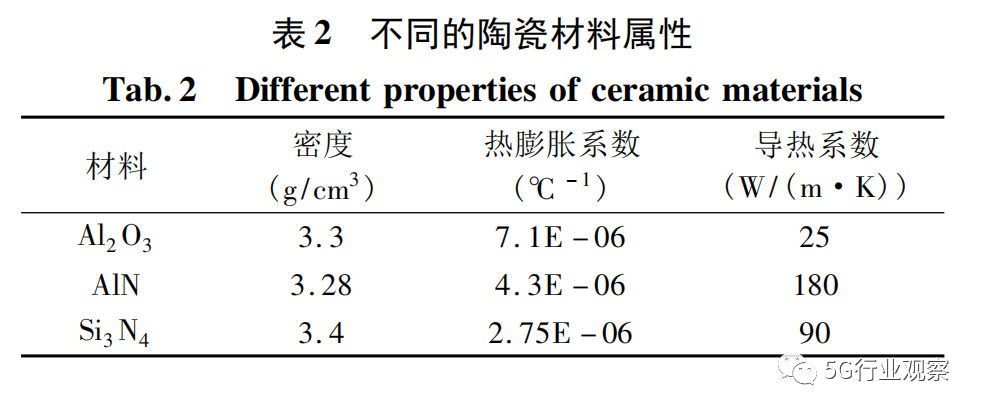
从表2中可知导热性能最佳为AlN陶瓷基板，而热膨胀系数最小为Si3N4陶瓷基板，同时该材料的基板也是综合性能最佳的，但成本偏高，而Al2O3陶瓷基板工艺较为成熟，成本较低。以这3种陶瓷基板为变量，探究其对器件散热的影响，计算结果如图7。

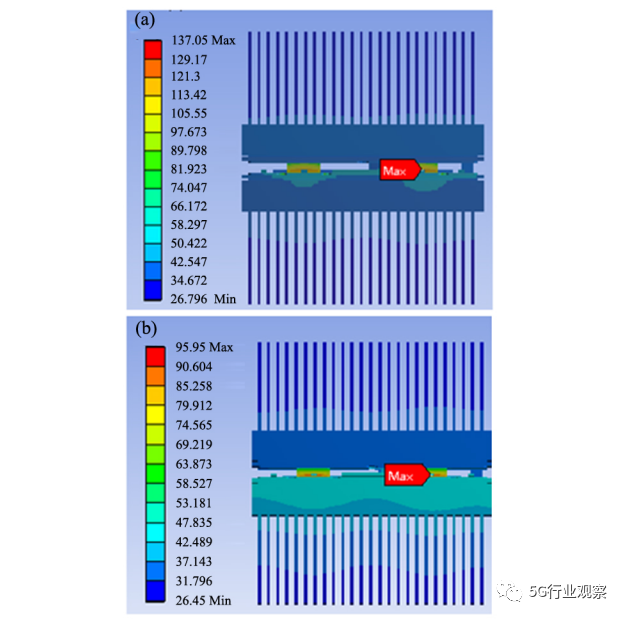
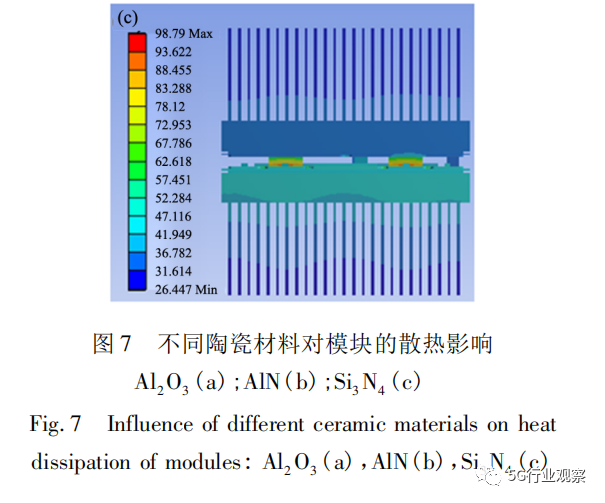
从左到右分别为Al2O3、AlN、Si3N4这3种陶瓷基板的计算模型，其中温度计算结果最高的是Al2O3陶瓷基板，其最高结温为137． 05 ℃，最低的是AlN陶瓷基板，其最高结温为95． 95 ℃，需要特殊说明的是由于Si3N4材料的力学性能较好，所以该陶瓷基板成品的陶瓷厚度只有其他基板的一半，以此来提高基板的散热能力，正如计算结果图7所示，其最高结温与AlN相差仅有3 ℃。

2.5不同银浆厚度对器件最高结温的影响

在本实验中的器件有着三层纳米银浆，分别连接着下基板、芯片、钼片缓冲层、上基板，如图1所示。在器件的制样中采用的是纳米银浆焊料，故本实验计算同样采用纳米银，将纳米银浆厚度作为自变量，最高结温作为因变量，厚度范围在0． 01 ～ 0． 1 mm，结果如表3所列。

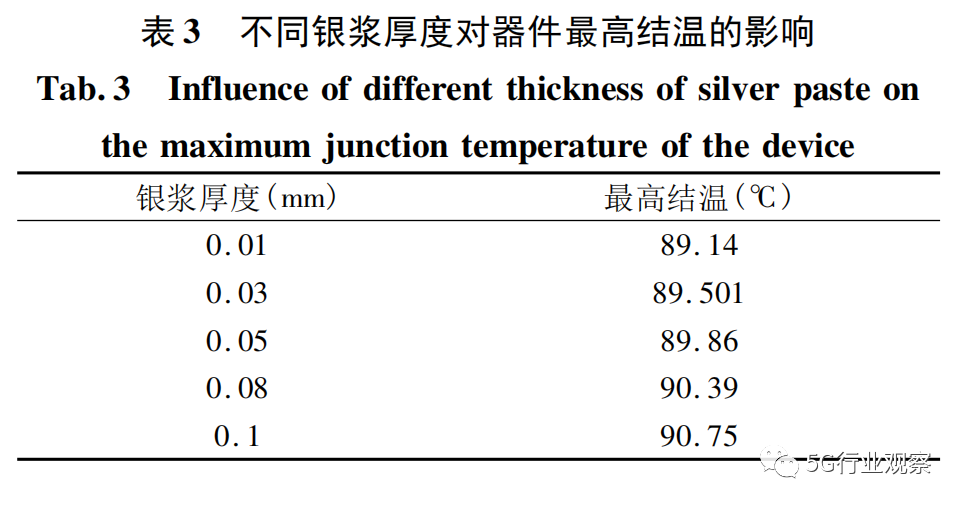
随着银浆厚度的减小，器件的最高结温整体趋势也在缓慢地下降，但效果并不明显，可以发现0． 1 mm的银浆厚度与0． 01 mm银浆厚度的器件最高结温相差不超过2 ℃，由热量在内部热传导时的热阻公式(3) 来描述:

Ｒ=L /(λA) (3)

式中:Ｒ为热阻;L为银浆厚度;λ为导热系数;A为银浆面积。当银浆厚度增加，热阻变大，温度随之上升，但由于银浆相对器件整体的热阻过小，并无法使温度波动太大，当银浆厚度为0． 01 mm时，Ｒ0． 01仅为0． 004 K/W。综上银浆厚度对器件的最高结温影响很小，无法作为器件对银浆厚度选择的重要依据，银浆厚度除了对器件温度有影响之外，对连接物体的应力同样也有影响。

2.6热应力分析

2.6.1不同银浆厚度对热应力的影响

银浆厚度对器件的最高结温的影响并不明显，然而对银浆的连接物体应力的影响尚未明确，需要进一步仿真计算。为排除其他因素对连接物体的热应力计算结果分析造成影响，在计算前对模型进行简化，使误差减少。本次计算的银浆同样采用纳米银浆，银浆厚度范围仍在0． 01 ～ 0． 1 mm。为简化计算，假设器件处于150 ℃的高温环境下。

将纳米银浆厚度作为自变量，其他重点关注部位的热应力作为因变量，计算结果如表4所示。

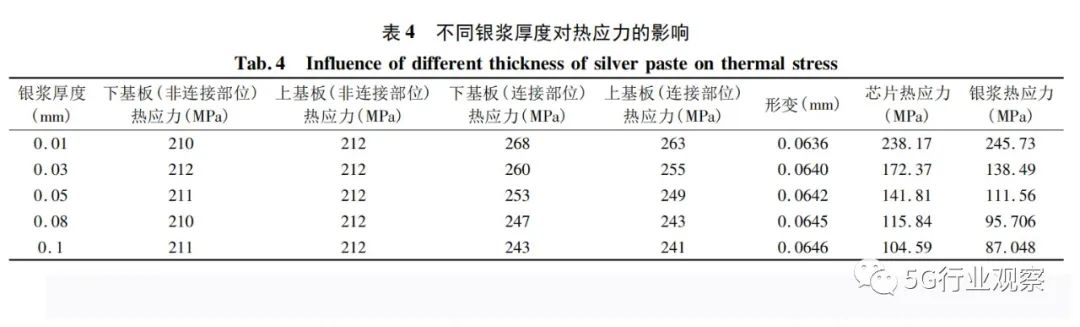
从表4可以看出，银浆厚度对芯片、基板连接部位的应力影响较大，而对基板非连接部位的应力计算结果并不影响，这说明了该模型基板非连接部位与银浆厚度的无关性，从而可以减少计算结果所带来的误差，保证计算数据的严谨性。而重点关注的连接部位的应力则是随银浆厚度的增加而减少，结果如图8所 示。上、下基板的连接部位的应力随银浆厚度增大而减小的趋势比较缓慢，芯片与银浆两个部位的应力下降幅度最为明显。当银浆厚度从0． 01 mm增至0． 1mm时，芯片与银浆的最大等效应力分别可下降56%和64%，这充分说明银浆厚度对应力的影响比较大。同时，银浆厚度对器件整体形变的影响可以忽略不计。

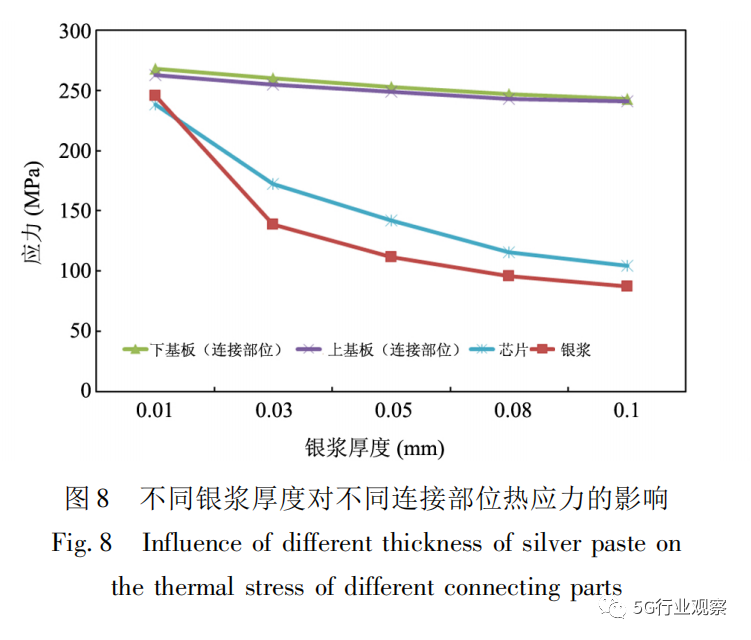
综上所述，银浆厚度对应力的影响可成为器件选择银浆厚度的重要依据。理论上银浆厚度在实验计算的范围当中选取0． 1 mm可达到最佳优化效果，但考虑芯片的厚度以及爬浆过高会导致短路，综合器件的制样情况最终选取0． 08 mm的银浆厚度。

2.6.2金属垫块结构对热应力的影响

银浆厚度对器件的最高结温的影响并不明显，然而对银浆的连接物体应力的影响尚未明确，需要进一步仿真计算。为排除其他因素对连接物体的热应力计算结果分析造成影响，在计算前对模型进行简化，使误差减少。本次计算的银浆同样采用纳米银浆，银浆厚度范围仍在0． 01 ～ 0． 1 mm。为简化计算，假设器件处于150 ℃的高温环境下。

器件可通过双面封装增加散热通道与换热面积，有效提高散热效率，使器件向更高功率与密度的方向发展，但同时双面封装结构必须承受更高的热应力。因此在双面封装结构中采用钼、钨等金属垫块作为缓冲层结构代替键合引线，优化结构应力。本实验通过无缓冲层、单层缓冲层、双层缓冲层3个模型去探究缓冲层对应力的影响，模型结构见图9，从左到右分别为无缓冲层、单层缓冲层、双层缓冲层3个模型，其中无缓冲层模型与双缓冲层模型都是上下对称结构。

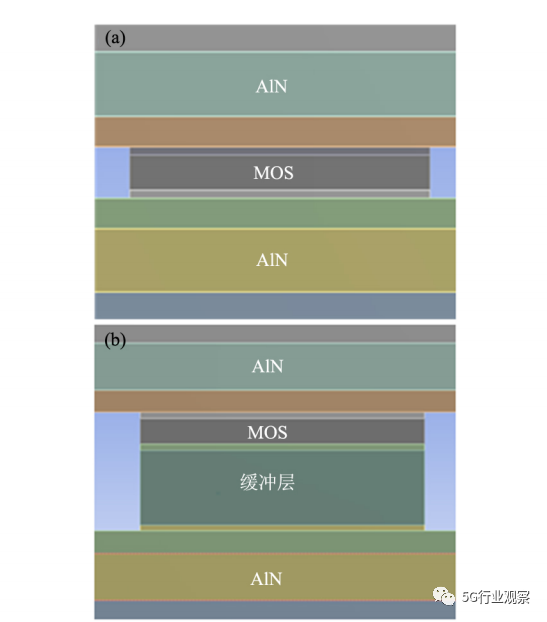
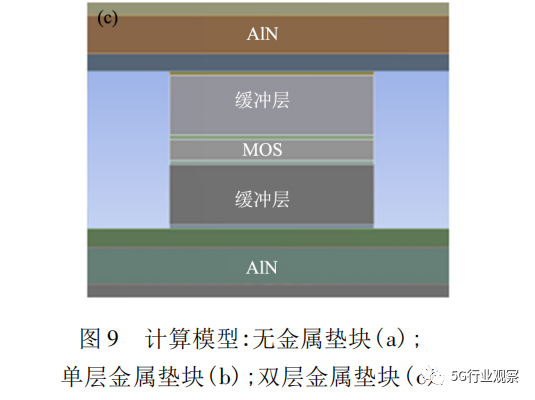
为避免其他因素造成对热应力计算结果的影响，对这3个模型进行简化。采用芯片发热的稳态结果作为器件的温度计算条件，温度条件计算所得结果:无金属缓冲层模型计算得最高结温为79． 36 ℃，单金属缓冲层模型计算得最高结温为90． 5 ℃，而双金属缓冲层模型计算得最高结温为108． 18 ℃。

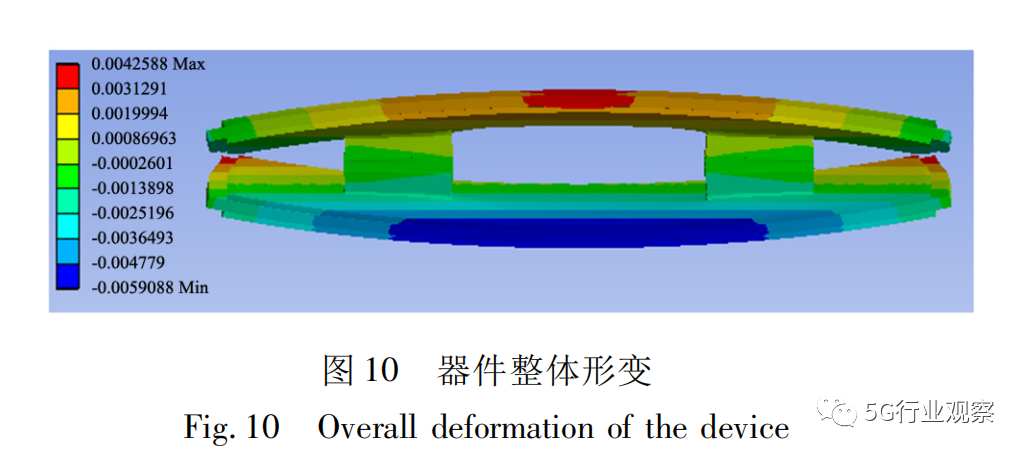
双层金属垫块模型的整体形变如图10所示，上下基板拱起的趋势较大，而器件的上下对称面位置形变量较小。该变形势必会对起连接作用的银浆造成较大的拉应力，当器件的芯片越靠近陶瓷基板，芯片也会受到较大的应力，当芯片处于对称面，这时芯片的热应力越会较小，银浆与芯片的计算结果见表5。

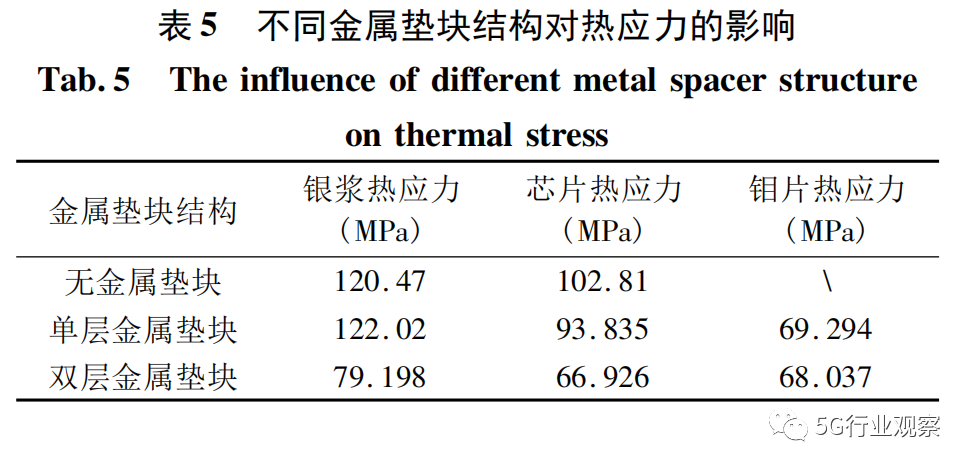图 11给出了无金属垫块结构、单层金属垫块结构和双层金属垫块结构与芯片或金属垫块接触的DBC铜层接触面的应力分布情况。其中图11(a) 为无金属垫块结构的基板铜层应力分布，图11(b) 为双层金属垫块结构的基板铜层应力分布，由于无金属层和双金属层的模型结构是上下对称的，所以上下基板铜层接触面的应力情况是一致的; 图11(c) 为单金属垫块上铜层应力分布图，即为与芯片接触的铜层应力分布，图11(d) 为单金属垫块下铜层应力分布图，即为与金属垫块接触的铜层应力分布，因为单金属层的模型结构并不对称，所以上下基板的应力情况并不一致。

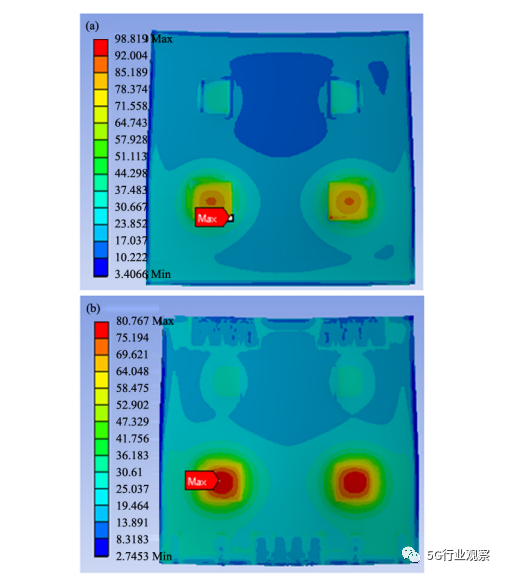
从图11中可以看到，无金属垫块的基板接触面铜层最大等效应力为98． 819 MPa，双金属垫块的基板接触面铜层最大等效应力为80． 767 MPa。结合上述有无金属垫块模型温度变化情况，双金属垫块结构的温度条件比无金属垫块结构高36． 3%，但其基板接触面铜层的热应力结果却比无缓冲层结构低18． 3%。

单金属层的上、下基板接触面铜层最大等效应力分别为109． 23 MPa、69． 51 MPa，这两者数值相差较大，这是芯片与钼片两者的热膨胀系数、温度差异等原因所造成的。与非对称结构相比较，上下对称结构的热应力实现相互抵消，使得器件整体应力偏小，然而由于器件电气线路等原因是无法实现完全对称结构的，但该结构具有优化器件应力的指导意义。

LED灯珠受芯片波长、荧光胶配比及均匀度的影响，不仅仅是不同批次、甚至同批次封装的灯珠特殊显色指数Ｒ9分布都会存在较大的波动。在LED灯珠色容差、压降、亮度、Ｒa等光电参数一致性很高的情况下，特殊显色指数Ｒ9的差异会影响颜色一致性，差异值取决于不同照明、背光产品的要求。普通照明产品如对颜色一致性有要求，在保证其他参数一致性的基础上，特殊显色指数Ｒ9的差值范围应该保持在15以内，对颜色一致性要求较高的商照或者背光产品，Ｒ9的差异建议不要超过10。所以对于Ｒ9的标准不应仅限于Ｒ9大于0，应根据产品应用的实际效果对Ｒ9的范围进行界定。

3结论

本文主要研究的是SiC双面封装模块的散热能力提升及其热应力优化，对于模块的散热，旨在通过提高模块的热对流系数、散热器模型的优化以及器件材料的选择等种种方法以降低器件的芯片结温，在器件热应力方面，针对应力集中现象比较严重的焊料层，以及器件缓冲层金属结构进行优化，从而使器件的应力有所下降。本文研究结论主要有:

(1) 基于本器件的计算环境，热对流系数为1000 W/(m2·K) 是一个较大的值，虽肋片式散热器换热比针式散热器差，但在导热方面肋片式效果更佳，故在本研究中肋片式散热器效果更好。

(2) 对于基板材料的选择，无论是从散热还是应力上，做薄后的Si3N4基板是最佳的选择，但考虑成本问题，AlN基板也能满足散热和应力要求。

(3) 在探究银浆厚度对应力的影响中，发现随银浆厚度增加，与银浆接触部位包括银浆的应力值都有所下降，综合考虑爬浆导致芯片短路，故最终选取银浆厚度为0． 08 mm为佳。

(4) 对于金属层结构的优化，发现当器件的整体结构上下对称时，可减少基板18． 3%的热应力，上下对称结构可使部分的内应力相互抵消，从而减少应力。

通过本文对功率器件热设计的研究优化，进而提高功率器件的可靠性，但是在散热器与应力研究上可以更深入。总体上，本文为功率器件的热设计提供了一定的参考，具有一定的指导作用。

来源：《中国照明电器》期刊-第2期

作者：杨 宁1，2 ，詹洪桂2 ，谢健兴2 ，王冠玉2 ，陈晓仪2 ，张 超2

1． 华南理工大学机械与汽车工程学院

2． 佛山市国星光电股份有限公司