COMPARE SPECIFICATIONS
通常,我们会将spec和设计实现进行比较。Spec相对来说比较抽象些,可以是些SVA的assertion,RTL model或者一些HVL,比如systemc等。而implemenation通常是RTL代码或者网表。
图1是一个简单的checker,A和B分别表示两种spec,它们接收相同的输入(Input),checker比较二者的输出是否相等。如果找到一个输入序列导致输出比较失败,就是找个了一个反例(CounterExample),工具会将此反例,包括相应的输入记录下来,呈现出来。这个checker其实是个黑盒(Black box),因为我们无法观察A和B内部的状态或者信号(白盒White box则可以)。
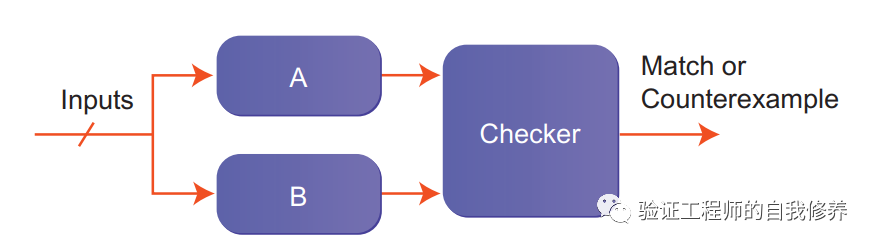
图1simple checker
如果A和B足够简单,那我们可以测到所有可能的情形,或者用Formal Verification来判定二者完全等价。同时,我们也可以借助这个等价来简化一些复杂的的问题,例如图2所示,一个更加复杂的系统,里面包含了A和B。
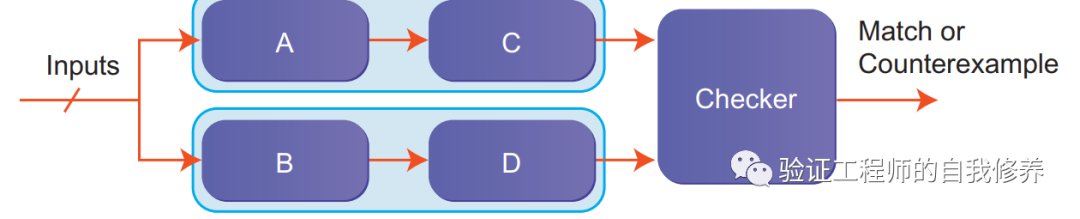
在这个例子中,因为我们先前已经证明了A等价于B,我们可以做下简化操作,把A和B从系统中拿掉,简化成C和D的比较,如图3所示。当然,C和D的输入(Inputs’) 与原始的输入(Input)已经有了很大的差别。这种divide and conquer 策略在FV中经常使用,主要用来简化分析大的design。

我们可以把上下方框想象成Spec和Implementation,这样的比较输入和输入我们可以判定implementation与spec是等价的,设计符合我们的要求。这个一个典型的formal equivalence verification (FEV) 。不过,通常Spec和Implementation不会出现这种理想的等价情况。
CONES OF INFLUENCE
如果我们把一些把相干的逻辑分别考量,验证复杂度能大大简化。比如,我们有个硬件,实现加法和乘法运算;在跑simulation的时候,我们可能造不同case侧重不同的点,有点测加法,有的测乘法。如果我们加法和乘法拆分出来,单独验,效率定能大幅提升,但在simulation里面不太现实,因为这需要造几套验证环境。
FV则能比较好的支持这种拆分,FV工具读取property,将设计里面一些与当前property不相关的逻辑移移除掉。这个叫cone of influence 简化。如图4所示,我们只考量result输出的时候,很多逻辑对这个输出没影响,我们可以把它们简化掉。如果design特别大的话,这种可以极大的简化复杂度。
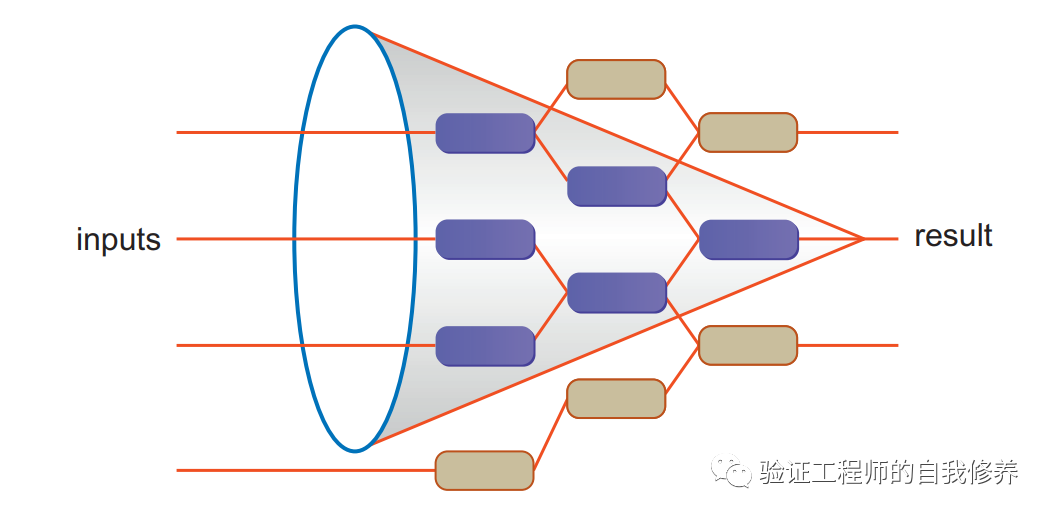
FV工具也可以支持用户自定义的简化,而非自动简化。例如有个输入,我们可以绑定成某个固定的值。这样逻辑也能大大简化。
BDD
BDD(binary decision tree),顾名思义,用树形结果来表示电路的逻辑。如果去观察一些电路的真值表如图5,会发现有很多redundancy,很多行都是0。BDD可以表示相同设计的同时,移除一些冗余的逻辑。BDD是一种范式(canonical ),等价设计的BDD是一样的;如果两个电路的BDD一样,那么可以判定二者等价。BDD算法是第一代Formal 工具常用的算法。
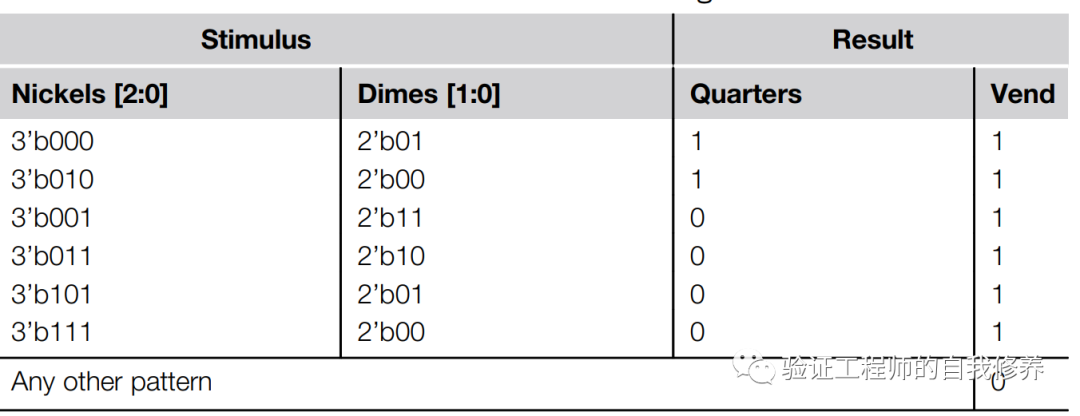
我们以一个MUX为例来说明BDD,如图6所示,一个MUX逻辑的BDD算法, xyz为输入,最下面一行为输出。类似于红黑树,每一个分支左侧代表下一输入变量为0,右侧代表输入为1.
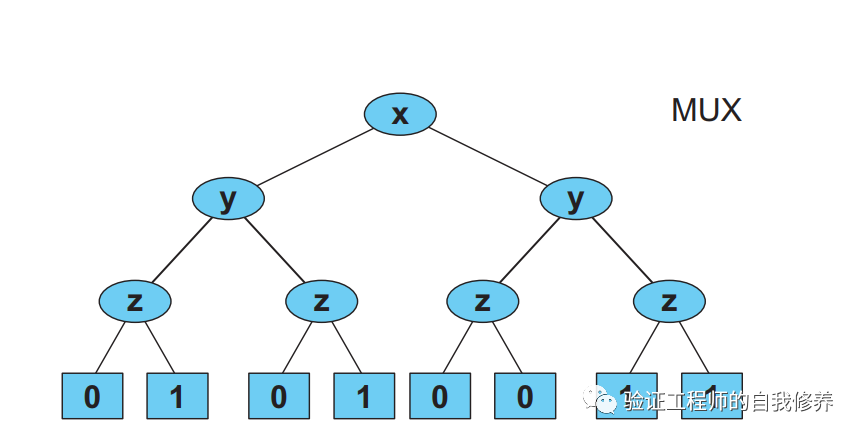
我们把输出为0和1的做下merge,如图7所示。
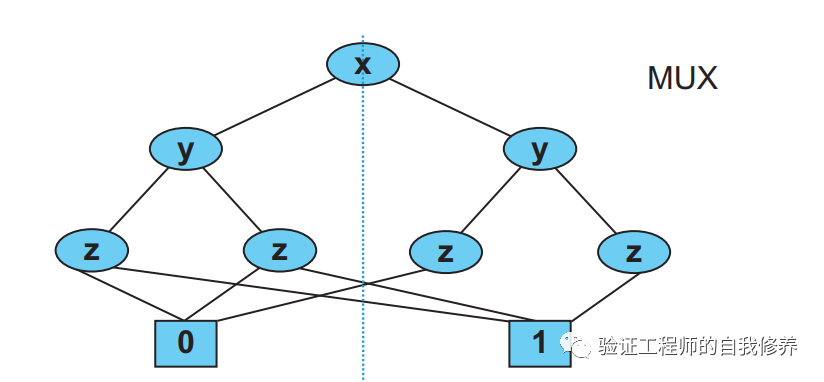
进一步观察,左侧两个z,无论取值如何,输出都是一样,说明父节点y不影响结果。同理,对于观察右侧,z节点多余。于是,我们可以进一步简化成图8这样的。
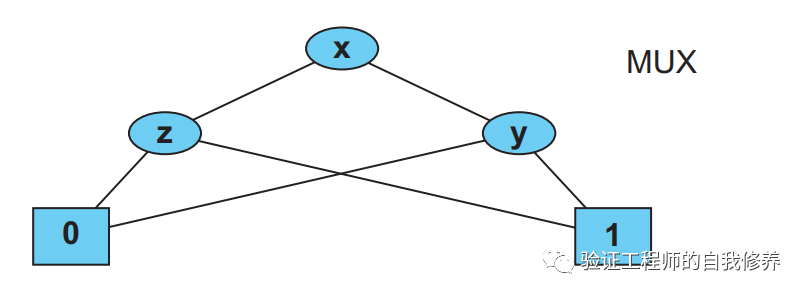
当然,如果选择变量的顺序不一样,我们得到的BDD的大小会有所不同。如果我们选择z->x->y的顺序的,我们将得到图9这样的BDD。对于一些大的design来说,如果顺序选择不当,可能导致指数爆炸。通常用Heuristic-based 算法来寻找最佳的变量顺序。比如根据电路的拓扑结构来,根据变量的相关性来映射。另一种方法是尝试将每一个输入变量替换0或者1,看看哪个精简的程度更大些。
对于大而复杂的设计来说,提取BDD仍然是一件很艰难的工作,或许随着输入的增加而指数级增长。
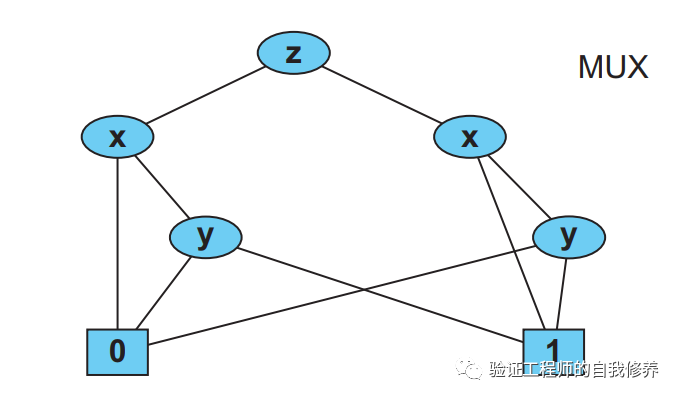
COMPUTING A BDD FOR A CIRCUIT DESIGN
如果我们有真值表,我们可以很快速的提取出BDD。但大部分电路,我们没那么容易算出真值表,尤其对RTL而言。庆幸的是,我们将根据基本的逻辑(与、或、非)的BDD组合起来,算出更大设计的BDD。
基本的与或非逻辑的BDD,参见图10所示。
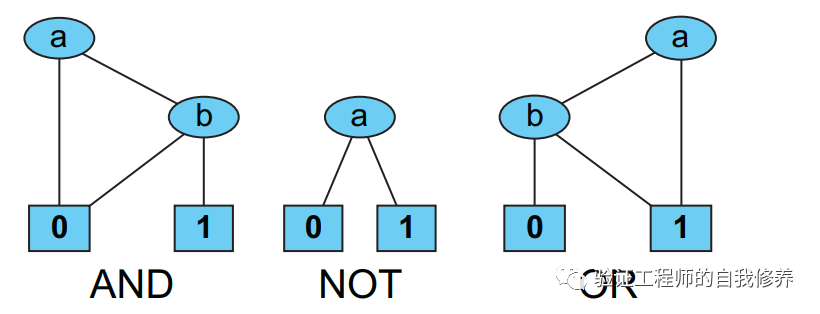
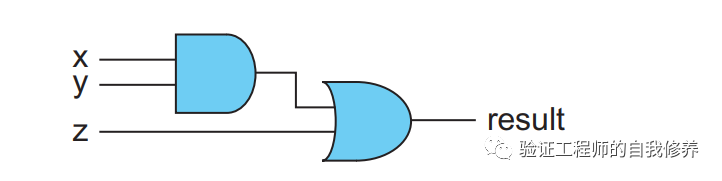
例如,我们以 (x&&y)||z 为例,电路如图11所示。将这些基本门电路组合在一起,就是这个电路的BDD,参见图12.
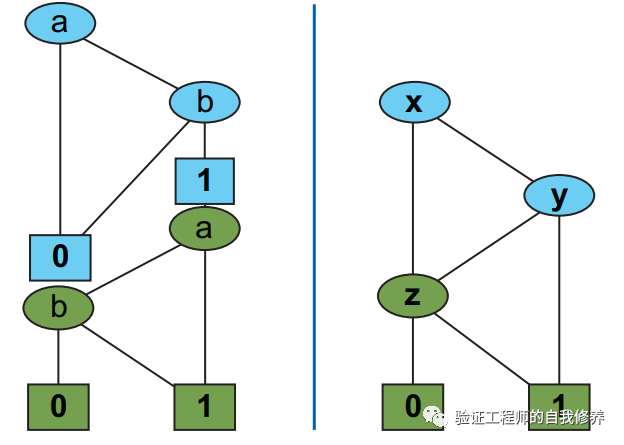
MODEL CHECKING
Model checking是FV工具分析一段时间内时序逻辑的主要方法。给定properties ,model-checking 会去搜索可能的未来状态,然后判定是否违反这些property。
首先创建初始状态的BDD,然后根据相应的逻辑推导出下一个状态的BDD,不断重复这个过程(reachability ),直到所有的状态都加进来。如果遇到vilation,FV会倒推回去,给出一个反例。
model checker 可能出出现三种情形:
设计符合spec
有violation,并给出反例
逻辑爆炸,无法证明;只能推测N个cycle没有violation
BOOLEAN SATISFIABILITY
BOOLEAN SATISFIABILITY,即SAT,它可以更快的举出反例。
假设我们有这样的spec和implemenation:
implementation = !(!a&&c || a&&!b) requirement = !a&&!c || b&c
即:
!(!a&&c || a&&!b) -> !a&&!c || b&c
p -> q 等价于 !p || q
(!a&&c || a&&!b) || (!a&&!c || b&&c)
SOLVING THE SAT PROBLEM
对于很多表达式,证明其成立可能比较困难,但找反例则会简单的多。如果我们写成AND形式,那只需要有一项为0,则表达式为0.
**Conjunctive normal form (CNF) **表达式是写成||形式,各个item或在一起,也称作product-of-sums 。可以将AND类比成乘法,OR类比成加法。比如下式就是个CNF:
(a||b||!d)&&(!b||c)&&(a||c)
所有的bool逻辑都可以表达成CNF形式。
我们一个或门为例,输入为a,b,输出为c。它的基本逻辑是:
a -> c b -> c !(a||b) -> !c
改写一下:
(!a||c)&&(!b||c)&&(a||b||!c)
我们建立一个真值表,把输入一个个赋值进去,看看是否成立。比如a=0, b= 0, c = 0。但如果变量比较的多的话,算法会指数爆炸。
THE DAVIS-PUTNAM SAT ALGORITHM
一个个枚举显然不太合理,一个简单的思路是先考虑一个变量,这样就拆分成两个子问题:一个a=0和一个a=1的情形。不断重复这个过程,直到证明或者有违规。
SATDivide&Conquer(formula)
If the formula evaluates to 1
{Return Success!}
If the formula evaluates to 0,
{Return Failure, hope another assignment works.}
Else
{split the problem on some variable, v.
SATDivide&Conquer (formula replacing v with 0)
SATDivide&Conquer (formula replacing v with 1)
}
最坏的情形是把所有的都遍历一遍,但一般来说不需要。例如对于表达是(a||!b||c) 来说,如果将a赋值成1,整个表达等于1,不需要继续分析了。
一个典型的列子如图13所以
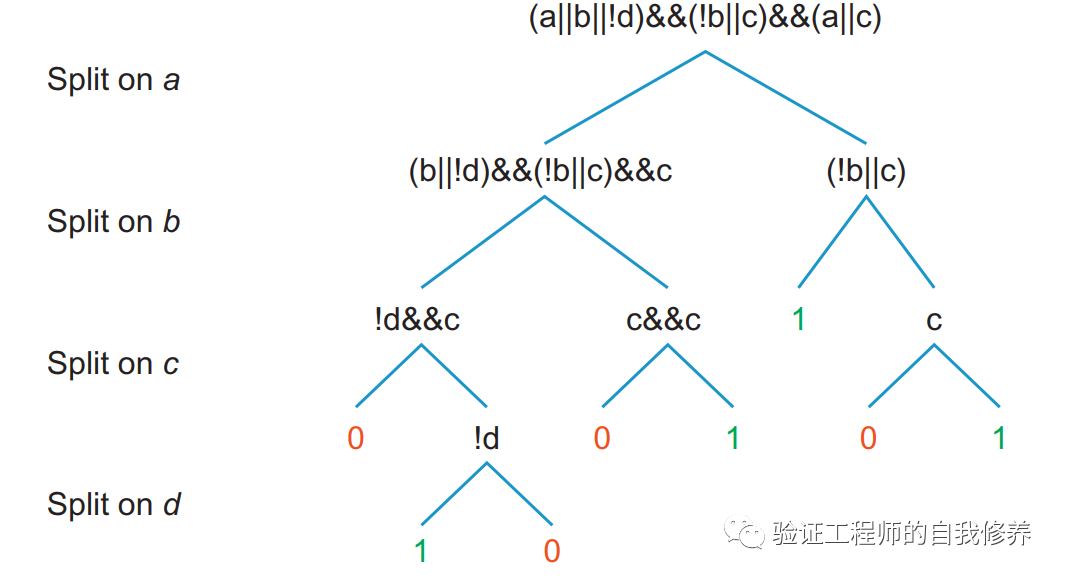
总结:
不要理解成formal是逐个枚举输入变量的值,formal实际上用的数学方法来证明的。
审核编辑:刘清
-
RTL
+关注
关注
1文章
385浏览量
59756 -
SPEC
+关注
关注
0文章
31浏览量
15792 -
BDD
+关注
关注
0文章
6浏览量
7524 -
Mux
+关注
关注
0文章
38浏览量
23371
原文标题:Formal学习笔记之算法基础
文章出处:【微信号:Rocker-IC,微信公众号:路科验证】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
Formal算法基础知识学习笔记
STM32各模块学习笔记
开关电源学习笔记 --- 目录





 Formal学习笔记之算法基础学习
Formal学习笔记之算法基础学习










评论