目前国内外基本都采用SOC来作为描述动力电池容量状态的内部参数。电池SOC估计是否准确对于电池来说关系重大,会直接影响动力电池使用寿命和电动汽车的行驶里程。但是电池SOC却很难在使用中直接测量得到,只能通过其它可以直接测量的电池参数估算得到。这就提高了SOC估计的难度,也使如何精准估计电池SOC成为了当下动力电池领域的研究热点。
卡尔曼滤波算法是有效的、经典的智能算法,能够实现最小方差的最优状态估计,目前被广泛应用于许多工程领域。由于其具有较好的估计精度和时效性,结合基尔霍夫定律搭建的二阶RC模型一起使用,已逐渐成为电池SOC估算研究领域的热点方法。考虑到卡尔曼滤波算法只适用于线性系统,应用到电池SOC中需要对其进行扩展,即扩展卡尔曼滤波算法(Extended Kalman Filter,EKF)。EKF算法的内涵:通过泰勒级数展开并忽略高次项的方法对非线性系统进行改造。
令非线性系统的离散状态方程和观测方程如下式所示:
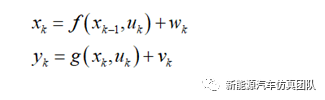
式中,xk表示系统在k时刻的状态向量,yk表示系统在k时刻的观测向量,uk表示系统在k时刻的输入向量,f(xk,uk)表示系统的状态转移函数,g(xk,uk)表示系统的测量函数,wk是系统的过程噪声,其协方差是Qk,vk是系统的观测噪声,其协方差是Rk。
对f(xk,uk)和g(xk,uk)进行泰勒级数展开后线性处理得到的系统状态空间方程为:
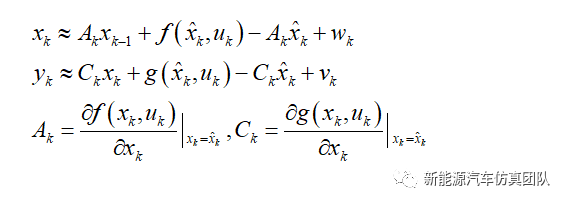
式中,Ak表示系统参数矩阵,Ck表示观测系统参数矩阵。
得到系统的离散表达式后,可利用EKF算法进行状态估计。
X_pre= [SOC_pre;U1_pre;U2_pre];
K=P_pre H' ((HP_preH'+R)^(-1));
X_upd= X_pre + K*(UL_ob-UL_pre);
P_update= (eye(3) - K*H)*P_pre;
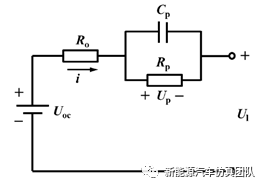
通过具体的参数辨识结果,结合EKF算法对SOC进行估计,需要将电池的两个RC环节的端电压以及SOC作为系统的状态变量。
SOC_upd= X_upd(1);
U1_upd= X_upd(2);
U2_upd= X_upd(3);
电池负载端电压为输出变量,对电池模型状态空间方程和观测方程进行离散化处理,得到电池系统离散化表达式:
A=[10 0;0 exp(-1/Tao1) 0;0 0 exp(-1/Tao2)];
B=[-11/(2.6763600);rp1*(1-exp(-delta_t/(rp1 cp1)));rp2 (1-exp(-delta_t/(rp2*cp2)))];
C1=8.3085SOC_pre^8-121.5774SOC_pre^7+402.8993SOC_pre^6-597.0354SOC_pre^5+463.6147SOC_pre^4-192.8896SOC_pre^3+40.3829SOC_pre^2-2.9747SOC_pre+3.4805; % 备注:OCV-SOC函数求导关系式
H= [C1 -1 -1];
同时,OCV-SOC的关系可表示为:
OCV=8.3085SOC^8-121.5774SOC^7+402.8993SOC^6-597.0354SOC^5+463.6147SOC^4-192.8896SOC^3+40.3829SOC^2-2.9747SOC+3.4805;
function [U1_pre,U2_pre,Tao1,Tao2]= fcn(R1,R2,C1,C2,U1_upd,U2_upd,I)
Tao1 = R1*C1;
Tao2 = R2*C2;
U1_pre = U1_upd*exp(-1/Tao1) + R1*I*(1-exp(-1/Tao1));
U2_pre = U2_upd*exp(-1/Tao2) + R2*I*(1-exp(-1/Tao2));
function [P_upd,SOC_upd,U1_upd, U2_upd] = fcn(Noise, UL_ob, UL_pre, P_old, SOC_pre, U1_pre,U2_pre, Tao1,Tao2)
Q = Noise(1); %过程噪声
R = Noise(2); %观测噪声
%%
%状态方程系数
A=[1 0 0;0 exp(-1/Tao1) 0;0 0 exp(-1/Tao2)];
B=[-1*1/(2.676*3600);rp1*(1-exp(-delta_t/(rp1*cp1)));rp2*(1-exp(-delta_t/(rp2*cp2)))];
P_last = [P_old(1) P_old(2) P_old(3); P_old(4) P_old(5) P_old(6); P_old(7) P_old(8) P_old(9)];
P_pre = A*P_last*A' + [Q 0 0;0 Q 0;0 0 Q];
%%
fn=@(x) 8.3085*x^8-121.5774*x^7+402.8993*x^6-597.0354*x^5+463.6147*x^4-192.8896*x^3+40.3829*x^2-2.9747*x+3.4805;
syms t1;
g=fn(t1);
g=matlabFunction(diff(g));
C1 = 8.3085*SOC_pre^8-121.5774*SOC_pre^7+402.8993*SOC_pre^6-597.0354*SOC_pre^5+463.6147*SOC_pre^4-192.8896*SOC_pre^3+40.3829*SOC_pre^2-2.9747*SOC_pre+3.4805;
H = [C1 -1 -1];
%%
X_pre = [SOC_pre;U1_pre;U2_pre];
K=P_pre*H'*((H*P_pre*H'+ R)^(-1));%计算卡尔曼增益
X_upd = X_pre + K*(UL_ob-UL_pre);
P_update = (eye(3) - K*H)*P_pre;
%%
SOC_upd = X_upd(1);
U1_upd = X_upd(2);
U2_upd = X_upd(3);
P_upd = [P_update(1,1) P_update(1,2) P_update(1,3) P_update(2,1) P_update(2,2) P_update(2,3) P_update(3,1) P_update(3,2) P_update(3,3)];
得到基于电池模型的离散状态空间方程后,结合扩展卡尔曼滤波算法,基于Simulink仿真,搭建电池SOC估算模块。通过EKF算法对电池SOC估算,首先根据随机工况定义系统的状态变量初值,以及恰当的噪声协方差矩阵Qk和Rk的值。然后,基于EKF算法通过k-1时刻系统状态估计值和k时刻系统的输入值uk,观测值yk,估计出k时刻的状态估计值。
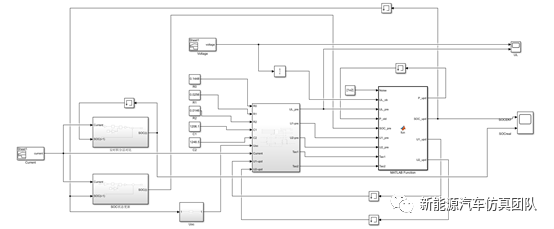
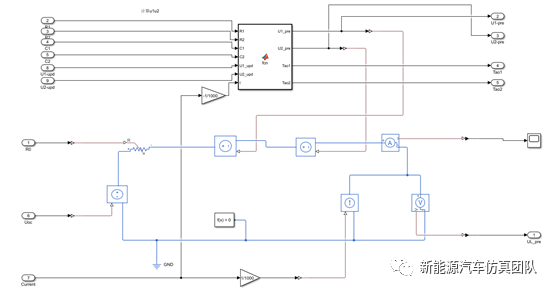
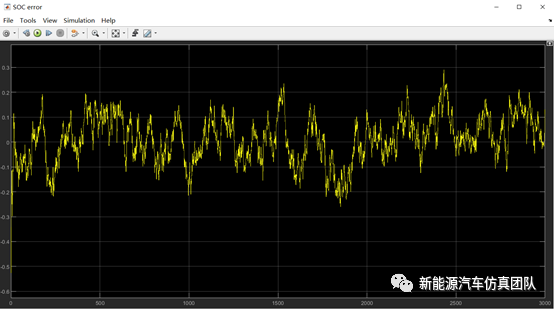
从图中可以看出,估计曲线非常快速地逼近到真值附近。说明该算法可以快速对初值偏差进行修正。即使在初值不清楚的情况下,依然能给出较为准确的SOC估计值。
-
电动汽车
+关注
关注
156文章
12226浏览量
232858 -
动力电池
+关注
关注
113文章
4556浏览量
78073 -
simulink仿真
+关注
关注
0文章
75浏览量
8624 -
卡尔曼滤波算法
+关注
关注
0文章
12浏览量
2128 -
电池SOC
+关注
关注
0文章
10浏览量
3610
发布评论请先 登录
相关推荐
基于Matlab/Simulink的二阶控制系统仿真研究
二阶有源低通滤波器_最简单的二阶低通滤波器电路图
复杂水电系统二阶振荡模式




 基于Simulink搭建二阶RC的EKF算法电池SOC估算模型
基于Simulink搭建二阶RC的EKF算法电池SOC估算模型












评论