支持向量机可求解二分类问题。当需要求解多分类问题时,支持向量机可将二分类问题的求解方式转化为多分类问题的求解方式。
多分类问题的求解方式:1类对K-1类、1类对另1类。
下文主要介绍1类对K-1类的具体方式 假设样本需要被分为K类,则需要构造K个支持向量机模型,即:
(1)第1个支持向量机模型将类别1分为一类,将2、3、4...K分为一类;
(2)第2个支持向量机模型将类别2分为一类,将1、3、4...K分为一类;
(3)第3个支持向量机模型将类别3分为一类,将1、2、4...K分为一类; …… (K)第K个支持向量机模型将类别K分为一类,将1、2、3...K-1分为一类;
再假设上述K个支持向量机模型,单一类别的标签为+1,其他K-1类构成的一类的标签为-1。
对上述K个支持向量机模型求解,可得出K个α和b的组合,可记为: {αi(k)}i=1~N,b(k),k=1~K 对某一样本X的分类,根据如下判别式: kmax=argmax∑αi(k)yiK(Xi,X)+b(k),k=1~K 其中,argmax函数值为使argmax右侧函数取最大值时自变量的值,即argmax∑αi(k)yiK(Xi,X)+b(k)的值为使∑αi(k)yiK(Xi,X)+b(k)最大时k的取值,即若x0= argmax(f(x)),则当x=x0时,f(x)取得最大值。(根据百度百科理解)
上述判别式的含义是:将测试样本输入到K个支持向量模型进行计算,并在k个支持向量模型中,筛选出某1类与该类对应的K-1类间隔最大情况的支持向量模型(即筛选{αi(k)}i=1~N,b(k)的值)。
将此支持向量模型计算出∑αiyiK(Xi,X)+b值所对应的标签作为测试样本的标签。(含个人理解)
例如:经过计算对比后,若某一测试样本的第2个支持向量机模型所对应的类别2与包含1、3、4...K类的类间隔最大(其两类间隔均大于第1、3、4…K个支持向量机所对应两类的间隔),则第2个支持向量机模型所对应的{αi(k)}i=1~N,b(k)的值为该测试样本的计算标签值的αi、b的值,最后,通过∑αiyiK(Xi,X)+b计算出该样本的标签。(个人理解)
1类对K-1类的策略容易导致训练样本不平衡的问题。
该问题出现的原因是:K个支持向量所分得的两类均为某1类和包含其他K-1个类的类,其他K-1个类的类的样本数量一般远多于某1类的样本数量,当两类样本数量处于较大不平衡的情况下,支持向量机会更倾向将样本分类至数量多的一类。
审核编辑:刘清
-
向量机
+关注
关注
0文章
166浏览量
20972
原文标题:机器学习相关介绍(20)——支持向量机(多类问题之1类对K-1类方式)
文章出处:【微信号:行业学习与研究,微信公众号:行业学习与研究】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
支持向量和多中心点非线性聚类的两大方法
基于可能性二均值聚类的二分类支持向量机
熵的二叉树多类支持向量机的漏洞分类
支持向量机的手势识别
基于单类支持向量机的织物瑕疵检测研究
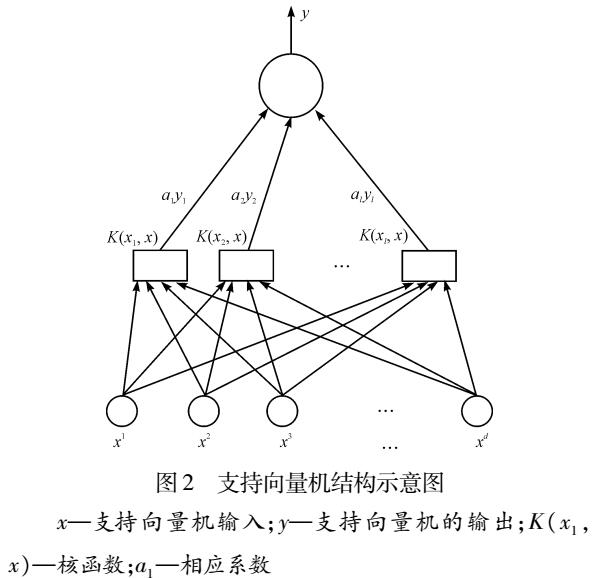




 支持向量机(多类问题之1类对K-1类方式)
支持向量机(多类问题之1类对K-1类方式)










评论