Delta-Sigma ADC与奈奎斯特速率ADC的工作方式略有不同。它依赖于过采样和噪声整形来实现高分辨率转换。
我之前的文章, 了解逐次逼近寄存器ADC,证明了这种奈奎斯特速率架构的弱点:它的精度和线性度以及最大有效分辨率受到DAC等模拟元件不完善的限制。
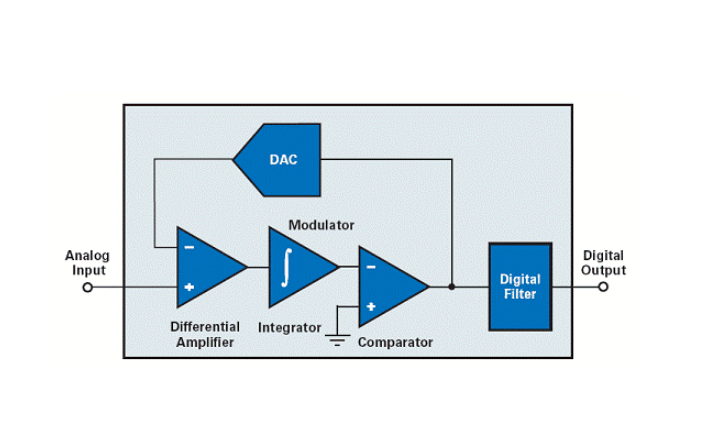
Delta-Sigma ADC所属的过采样转换器系列旨在克服奈奎斯特速率转换器的局限性。Delta-Sigma ADC由调制器,滤波器和抽取器组成,如下所示。Delta-Sigma ADC的数字化率约为75%。
通过引入更复杂的数字电路和过采样数据,他们试图降低对精确模拟元件的要求,这些元件可被视为其他ADC架构的限制因素。
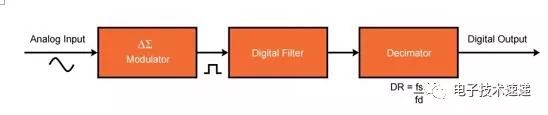
过采样
为了理解过采样的概念,需要在频域中进行分析。
如果我们考虑数据转换器输入端的正弦波示例,根据奈奎斯特准则,最小采样频率定义为信号带宽的两倍。
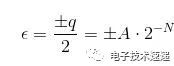
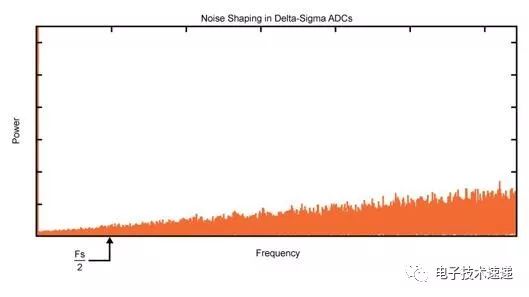
对于我们的正弦波示例,我们看到了感兴趣频率的峰值,但也有很多噪声,如下所示:
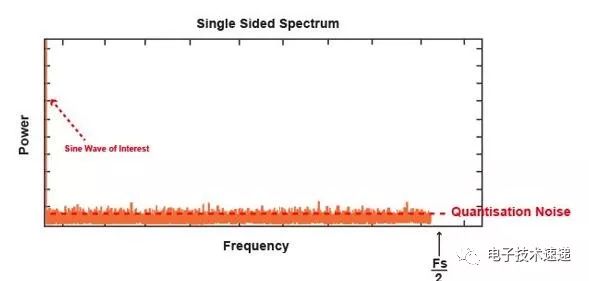
这种噪声称为量化噪声 (PDF),这是由于连续输入正弦波的样本只能采用由ADC分辨率决定的有限数量的离散状态。这种随机量化误差存在于奈奎斯特频带内,延伸到Fs / 2,可以描述为:
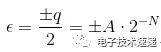
由此,我们可以将信号与量化噪声比确定为:
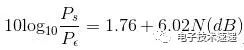
因此,在奈奎斯特速率ADC中,我们通过增加ADC的分辨率(用N表示)来改善SQNR(信号与量化噪声比)。有关这些公式的更深入解释,请参阅我之前的文章, 解密分辨率和采样率。
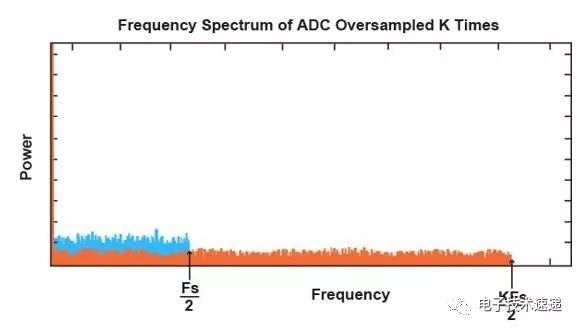
相反,如果我们现在将过采样频率从Fs增加到KF,如下所示,则区域Fs / 2中的量化噪声减小。SQNR实际上是相同的。
然而,量化噪声分布在较大的频率范围内。通过在Delta-Sigma ADC中集成滤波器,可以消除一些量化噪声。因此,在感兴趣的频率范围内量化噪声的这种减少使得低分辨率Delta-Sigma架构能够执行高分辨率模数转换。
如果我们将采样率提高4倍,则SQNR会提高6 dB。换句话说,每次我们将采样率提高四倍时,我们获得的相当于将ADC的分辨率加1位。仅使用过采样,为了实现12位分辨率,输入必须过采样4 11。或者,更一般地说,对于分辨率的N位增加,我们必须过采样2 2N因子。
幸运的是,另一种技术称为噪声整形,可实现超过6 dB的增益。
噪音整形
一阶Delta-Sigma调制器的框图如下所示。它由差分放大器,积分器,比较器和开关组成。开关或1位DAC将负或正参考电压切换到放大器的负输入。
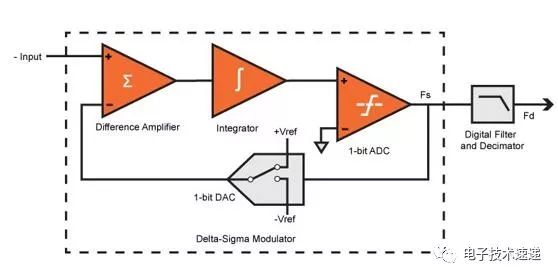
在这种架构中,如果输入信号增加,1位ADC(只是一个比较器)会产生一个。如果它减少了,它会产生零。因此,Δ-Σ调制器传输输入信号的变化或梯度。
与过采样一样,噪声整形最好在频域中进行说明。调制器的频域模型如下所示:
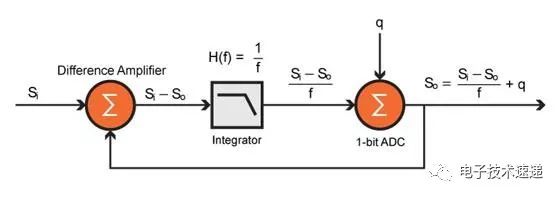
该架构中的积分器充当输入信号的低通滤波器。由于1位转换过程,量化噪声被添加到该滤波器的信号输出。调制器的输出可以使用下面的等式表示。
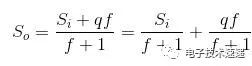
该等式中的第一项可以被认为是信号项,第二项可以被认为是噪声项。当频率接近零时,可以看出噪声项接近零并且调制器的输出接近S i。随着频率增加,噪声项接近q并且信号项接近零。因此,积分器充当量化噪声的高通滤波器。
高阶Delta-Sigma ADC,在调制器中具有多于一级的积分和求和,可用于实现进一步的噪声整形。
数字滤波和抽取
Delta-Sigma调制器将噪声推向更高的频率,以提高ADC的分辨率,并执行模拟输入到比特流的转换。数字滤波和抽取级用于滤除高频噪声并将数据速率降低到可用量。
使用的滤波器通常是一种称为sinc滤波器的平均滤波器。由于噪声已经被推到高频,因此低通滤波器响应用于衰减量化噪声。因此,已经获得了原始信号的高分辨率版本。
滤波器的输出数据速率与采样速率(Fs)相同。滤波器降低了信号的频率带宽。因此,根据奈奎斯特准则,大多数样本不包含任何有用的信息。
抽取是丢弃不必要的样本的过程,并且用作将数据速率降低到可用值同时根据奈奎斯特准则维护信息的机制。
Delta-Sigma ADC具有两种采样率,即输入采样率(Fs)和输出数据率(Fd)。Fs与Fd的比率称为抽取率(DR)。通过降低滤波器的通带并增加DR,同时保持相同的Fs,可以增加Delta-Sigma ADC的有效位数(ENOB)。同样,ADC的带宽可以以ENOB为代价来增加。
-
滤波器
+关注
关注
161文章
7884浏览量
179148 -
寄存器
+关注
关注
31文章
5377浏览量
121397 -
差分放大器
+关注
关注
8文章
450浏览量
52333 -
调制器
+关注
关注
3文章
843浏览量
45380 -
ADC转换器
+关注
关注
1文章
28浏览量
8366
发布评论请先 登录
相关推荐
Sigma-Delta ADC常见问题解答
高分辨率、低漂移和精密称重天平电子秤解决方案
请问24位的分辨率是否是所有ADC的极限?
扩展的Delta-Sigma ADC数据表?
单片机内置ADC实现高分辨率采样的方法
驱动高分辨率 SAR ADC

Delta-Sigma AD转换器的详细资料介绍
AN-241:AD7710高分辨率(24位)∑-Delta A/D转换器评估板

太秀了!单片机内置ADC实现高分辨率采样?





 Delta-Sigma ADC如何实现高分辨率转换?
Delta-Sigma ADC如何实现高分辨率转换?











评论