磁****集成技术
所谓磁集成技术,就是将多个电感、变压器绕在一个磁芯上;再通俗一点,就是把电感集成在变压器之中。主要的目的有:
- 减少体积提高功率密度
- 节省成本
- 提高效率,改善综合性能(寄生参数影响更小、设计得好还可以减小磁通脉动)。
最直观得益于这项技术的感受,莫过于手里体积越来越小的手机充电器和电脑充电器。而随着氮化镓GaN半导体的出现,开关频率可达到MHz级别,使得PCB变压器成为可能。
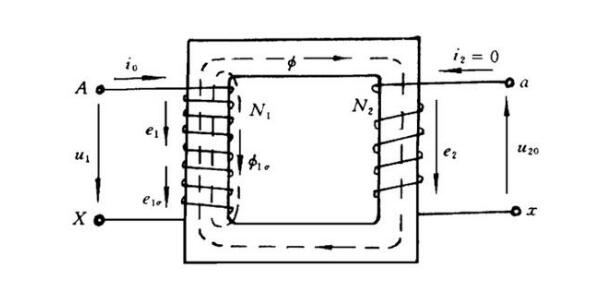
理想变压器并不存在,任何一个变压器都有漏电感,应用最为广泛的变压器T型等效模型中,也对漏电感进行了建模。
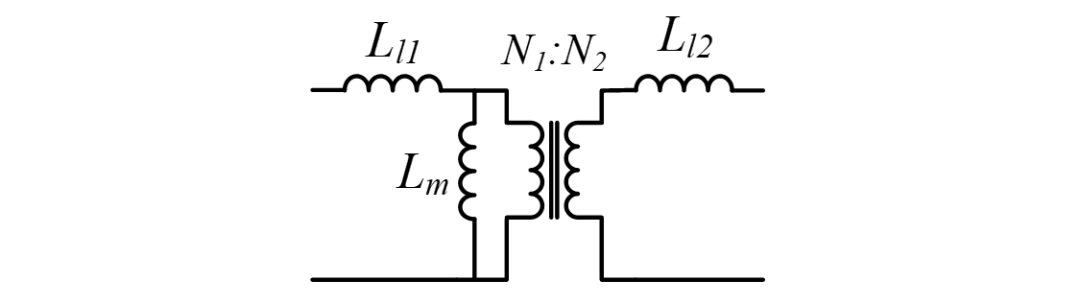
大多数情况,我们希望这个漏感足够小,但在有些情况我们需要利用这个漏感,如果这个漏感的特性和我们所需要的电感相同,也就完成了电感在变压器中集成。在某些情况,尤其是谐振变换器的应用中,电感需要精确设计,而在磁集成变压器中,则转变为对漏电感的精确控制。
磁****路分析
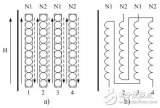
左下图是一种典型的磁集成变压器结构,有中心柱和两个边柱,为方便阐述,两个边柱我命名为A柱和B柱。中心柱和边柱都留有气隙,边柱柱气隙磁阻为 Rg1 ,中心柱柱气隙磁阻为 Rg2 。
(这里一共有四部分绕组,原边(primary)绕在A柱上的匝数记为 NPA ,副边(secondary)绕在B柱上的匝数记为 NSB ,以此类推)
原边绕组 NPA 、NPB和副边绕组 NSA 、 NSB ,非对称地绕在两个边柱上。
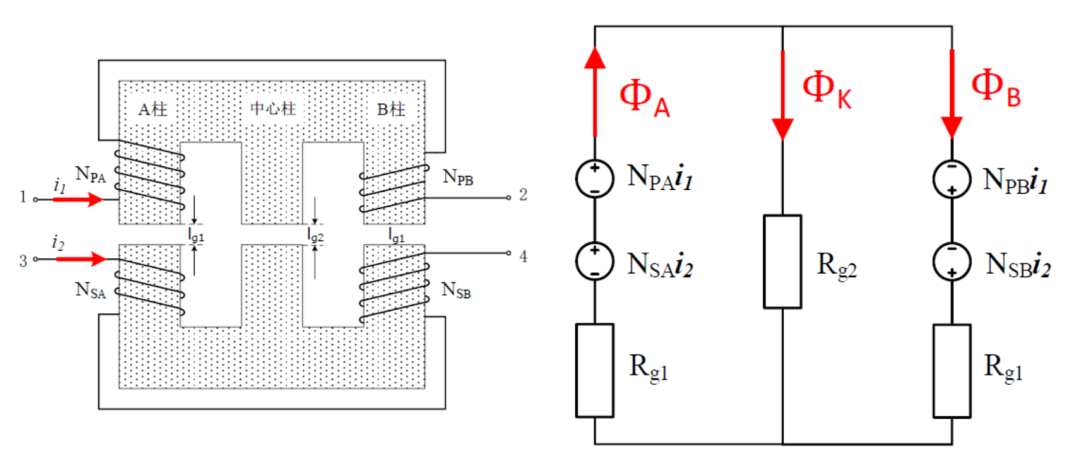
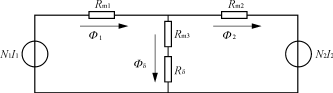
根据磁路理论,可导出为右上图所示的 磁路模型 。这里有一个重要的假设:磁芯磁导率足够大,磁导线集中在磁芯内部。
有电流的绕组转化为磁动势(MMF,Magnetic Motive Force)
MMF=NI
空气气隙转化为磁阻: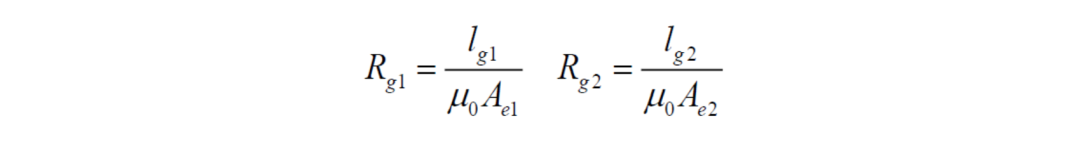
lg1 , lg2 ——边柱和中心柱的气隙长度
Ae1 , Ae2 ——边柱和中心柱的有效截面积
μ0 ——真空磁导率
上述两个公式可以由安培环路定律直接推导出来。
对照着磁路模型,可以直接用”支路磁通法”列出方程组:
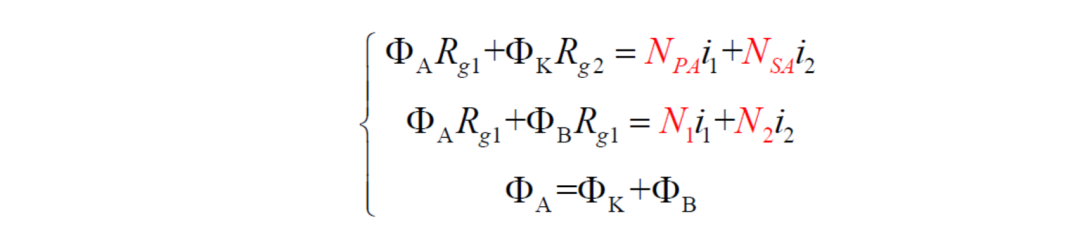
原边总匝数N 1 = NPA + NPB , 副边总匝数N 2 =NSA+NSB
可解得
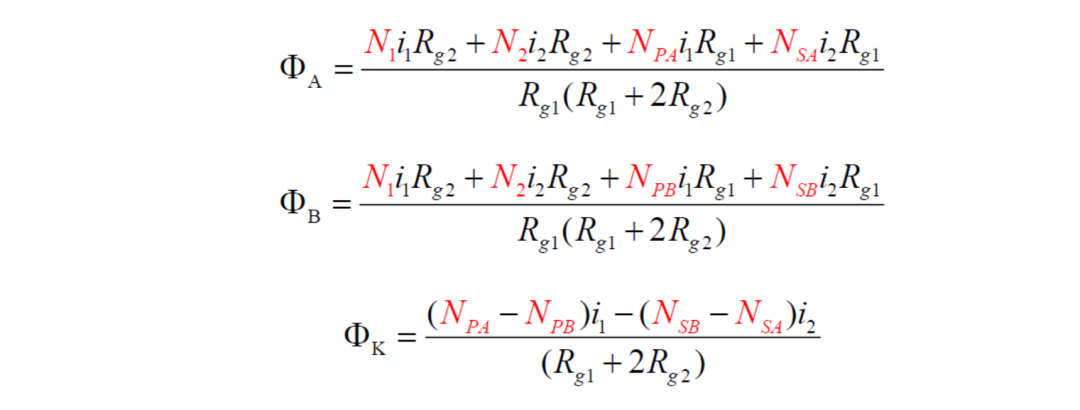
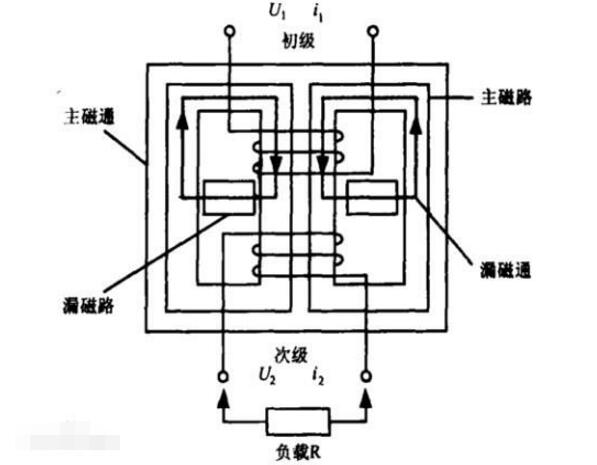
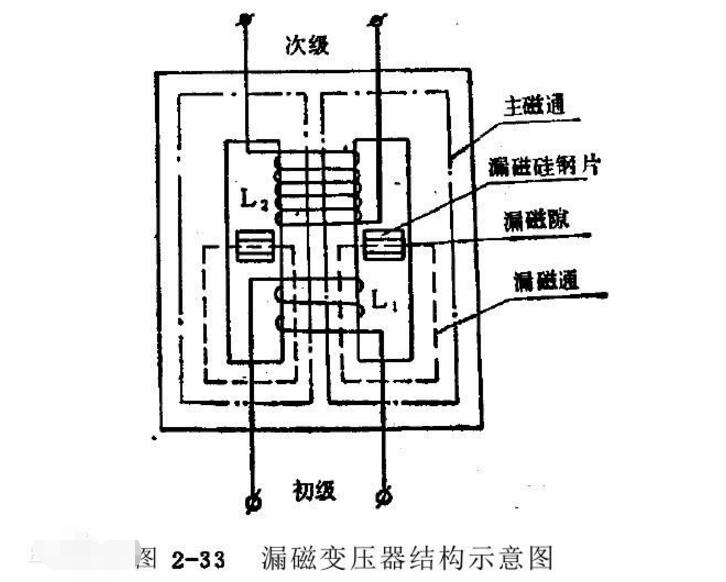
这里的ΦK就是漏磁通,前面提到变压器需要非对称绕制,这是因为如果对称绕制( NPA = NPB , * N SA * = NSB ),则理论上漏磁通为0。
这种结构的磁集成变压器能获得较好的EMC特性,是因为它的漏磁通集中在变压器内部的中心柱,没有对外辐射。
回到电路
到目前为止,似乎都是在分析磁通,还没有和我们所关心的漏电感扯上关系,再回到变压器的T型等效电路。
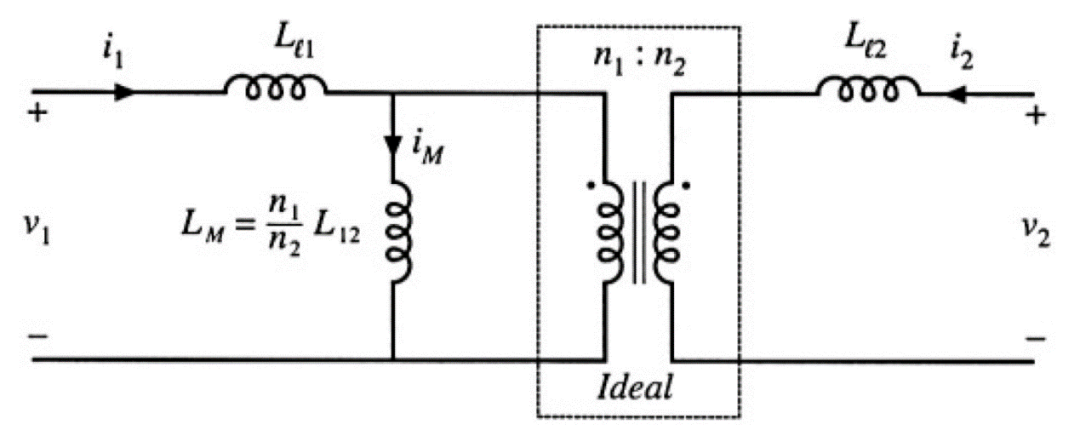
接下来我们需要找到磁路模型和电路模型之间的对应关系,用二端口网络来描述这个变压器(由于变压器为无源线性网络,一定是互易二端口网络,只有3个独立参数):
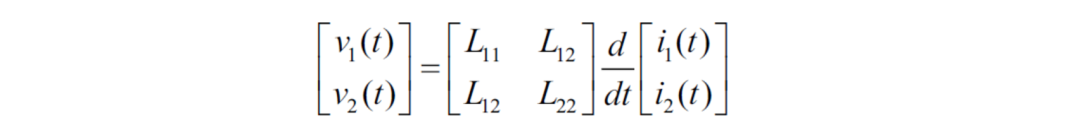
从磁路模型最后的结果继续,结合法拉第电磁感应定律有:
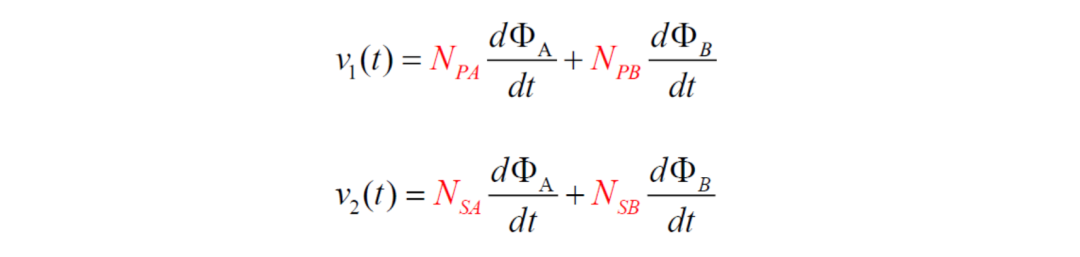
两种描述变压器的方式应当殊途同归,代入ΦA和Φ B ,可得到自感L 11 、L22及互感L12与绕组匝数之间的关系:
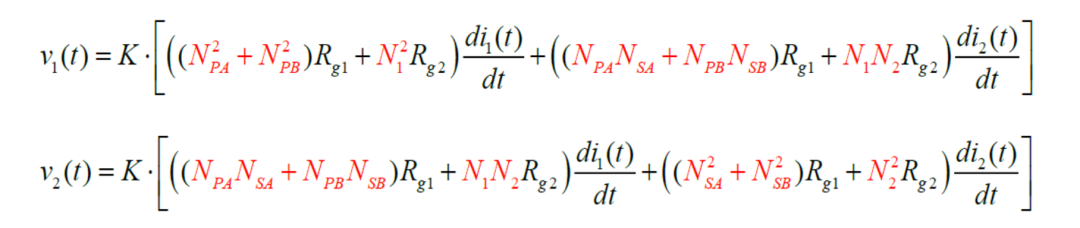
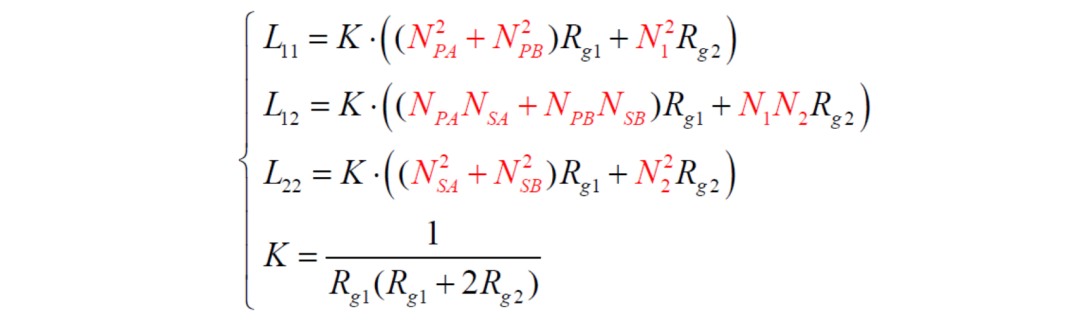
进一步我们就可以算出励磁电感和漏感了,总算大功告成。
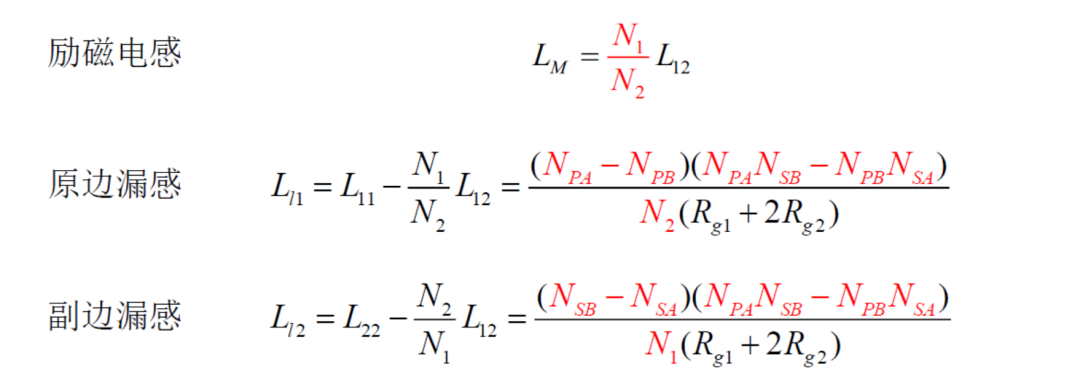
由此可见,漏电感的大小和 匝数绕法 、磁阻相关,而磁阻又和 截面积 、气隙长度相关,只要调整这些参数,就能得到想要的漏感大小。
如果A柱和B柱匝数相同,且变比为1( NPA = NSB , * N SA * = NPB ),则漏感的表达式可进一步简化为
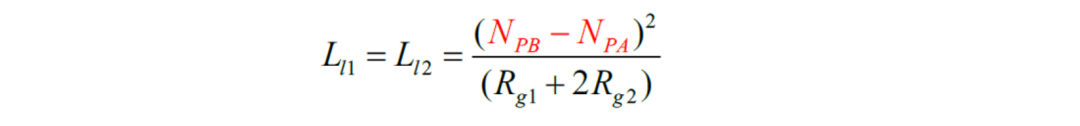
基于此,可进一步的归纳一些规律:原边漏电感的大小,近似正比于原边绕组在两个磁柱分别绕制 匝数差的平方 ,反比于磁阻。
符号也许不太直观,这里举个使用4层板的PCB变压器的例子
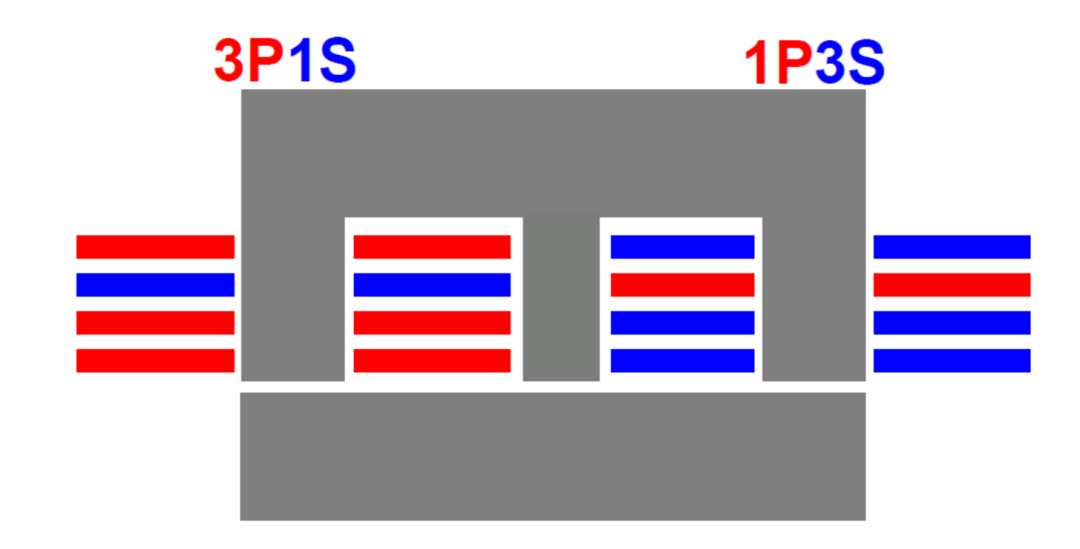
其对应的匝数为:

根据上文结论,可计算其励磁电感及漏感
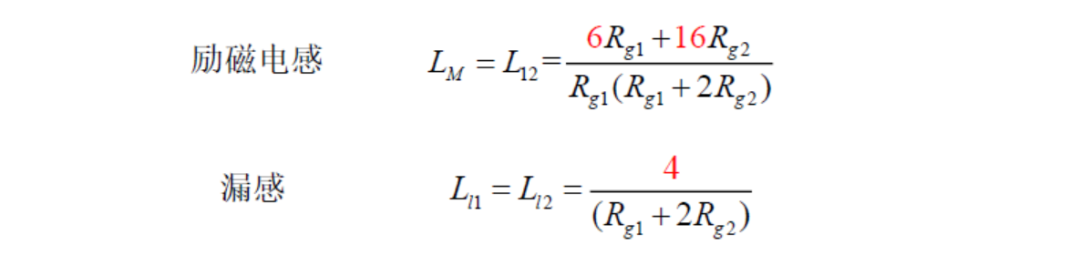
路****在何方?
此时一定应该有的疑问是:这样的分析方法真的足够精确吗?
很遗憾,经过样品实测,理论推导模型的结果与实际参数偏差约5%。这里我还使用到了有限元磁仿真软件Ansys Maxwell,得到的结果更加精确,与样品实测仅偏差<1%。
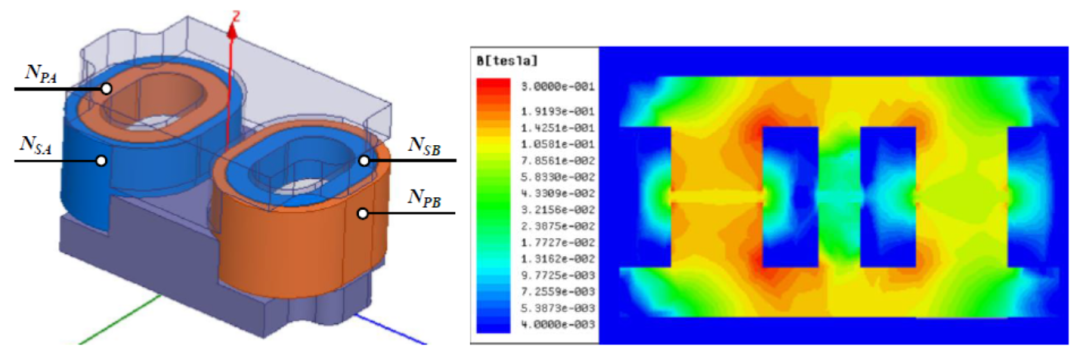
理论模型误差较大的原因在于,在分析的开始,我们假设了磁导率足够大忽略了空气磁路。
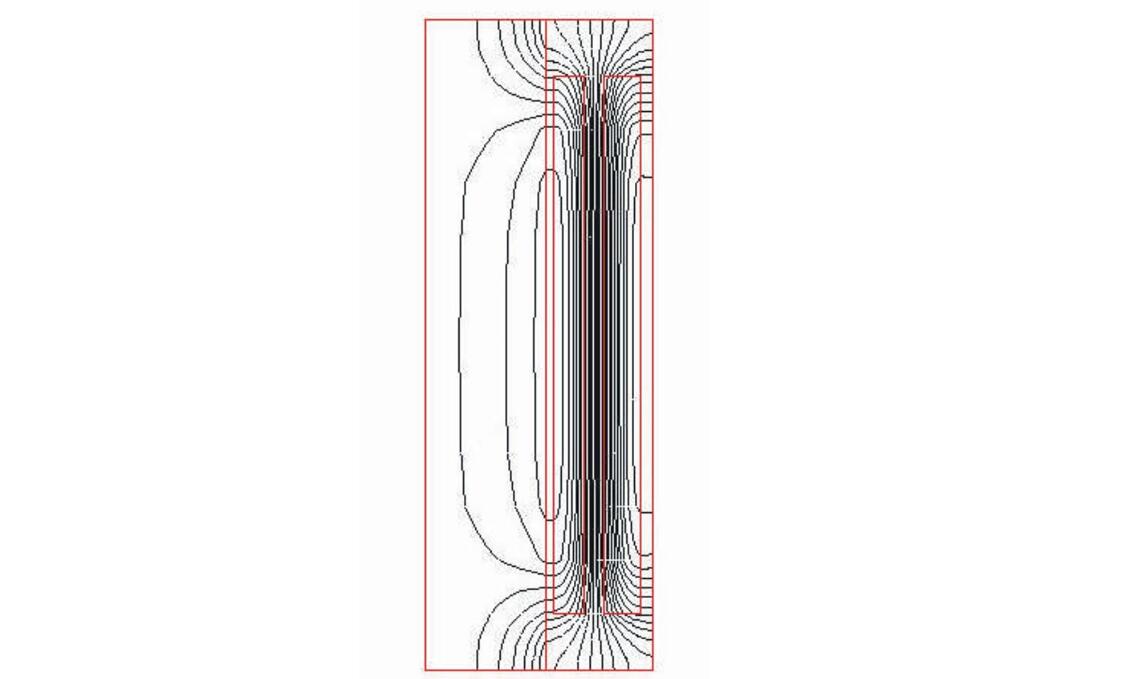
而事实上,磁导率不足够大时,导致气隙边缘效应、空气磁路并不能忽略,这点从仿真得到的磁场分布图中可以看出。
所以更为合理的设计方式是:先利用磁路推导的理论结果进行初步设计,然后在磁仿真中验证,这些公式的价值也在于指导调整设计参数的方向。
-
PCB设计
+关注
关注
394文章
4690浏览量
85777 -
谐振变换器
+关注
关注
1文章
73浏览量
15653 -
GaN技术
+关注
关注
0文章
38浏览量
7712 -
漏电感
+关注
关注
0文章
5浏览量
1304 -
变压器
+关注
关注
0文章
1144浏览量
4010
发布评论请先 登录
相关推荐




 求一种可控漏感的磁集成变压器设计方案
求一种可控漏感的磁集成变压器设计方案











评论