现实世界是一个模拟世界,我们需要将现实世界的模拟信号送给DSP,供其处理,这就需要模拟信号和数字信号之间的一个接口,ADC和DAC。随着DSP运算速度的加快,随之而来的是ADC的高速和高精度性能同样需要进一步提高。
ADC概况
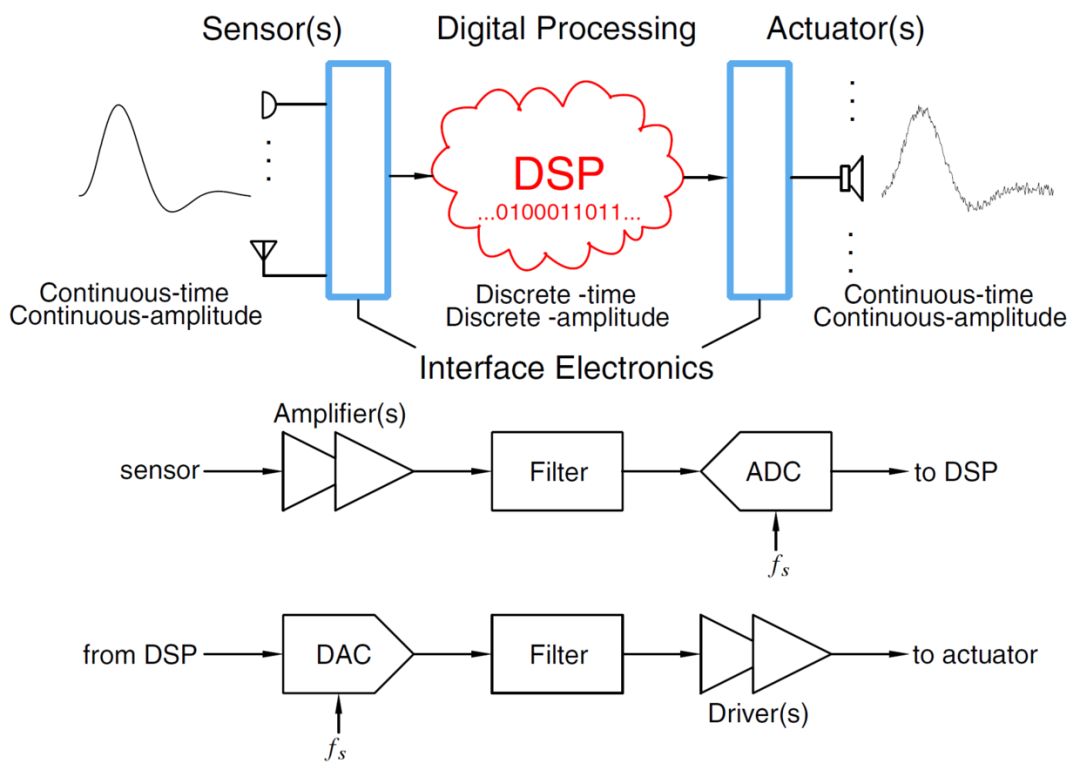
我们首先来看一下常规的电学系统框图,如下图所示,将现实世界的模拟信号感应、放大、滤波,再经过A/D转换,送给DSP处理,处理之后送给D/A,接着滤波、放大,送给执行器输出。这个系统具有普适性,当然如果考虑射频系统的话,再加上混频器即可。从这个系统框图中,我们可以看出ADC和DAC在整个电学系统中所处的位置和作用。其性能往往成为系统的瓶颈,设计高性能的ADC和DAC是非常有挑战的。
对于ADC来讲,主要的设计指标是精度和速度,遗憾的是,ADC的高速和高精度的满足是一对矛盾。不同结构的ADC要么是牺牲速度来换取精度,要么是牺牲精度来换取速度。当然,随着集成电路工艺的进步,以及电路设计人员的不懈努力,这对矛盾可以稍微缓解。
下图给出了常见的ADC结构及其可实现的精度和速度的对比情况,可以看到,没有一种结构可以同时实现高精度和高速度。本文接下来要介绍的是Σ-Δ ADC (Oversampled),它是以牺牲速度来换取精度的。

Σ-Δ ADC
为什么要首先介绍它呢?
正如题目所写,它是一个非常神奇而又有趣的结构,比如,它可以采用一个单比特的量化器,实现多比特输出的效果。和其它ADC结构相比,它是结构上的一种完全的创新,接下来我们一起来揭开它的神秘面纱。
在引入Σ-Δ ADC之前,首先引入一个实际的例子,以便大家理解。
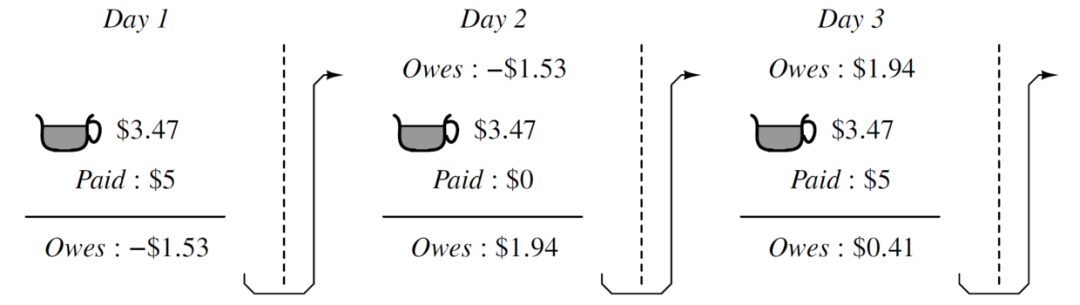
小孟在国外留学时,面对繁重的课业压力,他每天需要喝一杯咖啡来提神。幸好学校附近有一家百年咖啡老店,以醇香的味道深深地吸引着他。这家店一杯咖啡的售价是3.47刀,不支持刷卡支付(百年老店的倔强)。刚开始时,每天他付给店员5刀,然后店员给他找零1.53刀。日积月累,大家都觉得这样有点儿麻烦,店员需要准备大量的零钱以供找零,而小孟拿了一堆零钱也不是很方便。所以大家达成一个协议,小孟每次要不付5刀,要不不付钱,多付的或者亏欠的金额采用记账的方式。那么小孟什么时候需要付钱呢?每当小孟买完咖啡时,如果亏欠的金额超过2.5刀时,则需要付5刀,否则不需要付钱。这个过程可以用如下的示意图来表示,这里只给出了前三天的情况,后面的可以以此类推。其实大家可以想象到,虽然每天看起来彼此会互欠一些金额,但是长此以往,小孟所付的金额之和,和他所买咖啡的价格之和几乎是完全一样的,而且极大地方便了彼此。
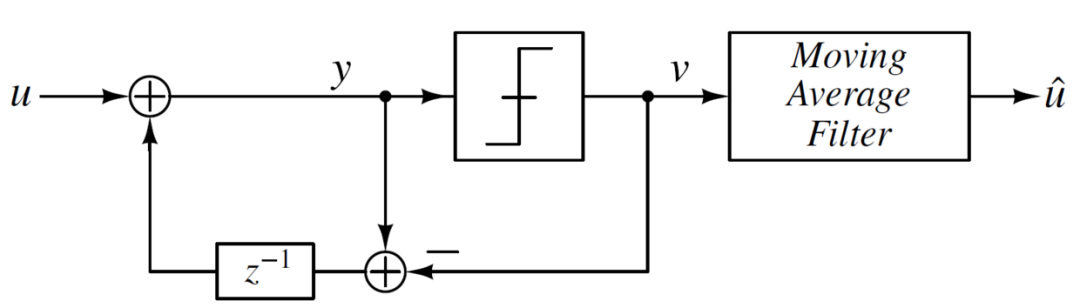
我们可以将上述过程转换为电路语言,如下图所示。其中,输入u代表一杯咖啡的价格,y代表当前交易时小孟欠店主的金额,将这个金额和2.5比较,来决定当前交易是否需要付钱,比较的过程可以用一个单比特量化器表示。v表示当前付款的情况,为0,或者为5,类似一个单比特量化器的输出结构。然后将y和v做差,表示当前交易结束后,交易双方互欠金额的情况,z^-1^为一个延迟单元,表示将这个互欠金额的结果送到第二天,并和第二天的咖啡价格累加,以此类推。如果将长时间v的输出结果累加并求平均,得到的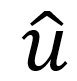 ,可以认为近似等于输入u。
,可以认为近似等于输入u。
从下图可以看出,随着循环次数的增加,v的平均输出非常接近输入u。
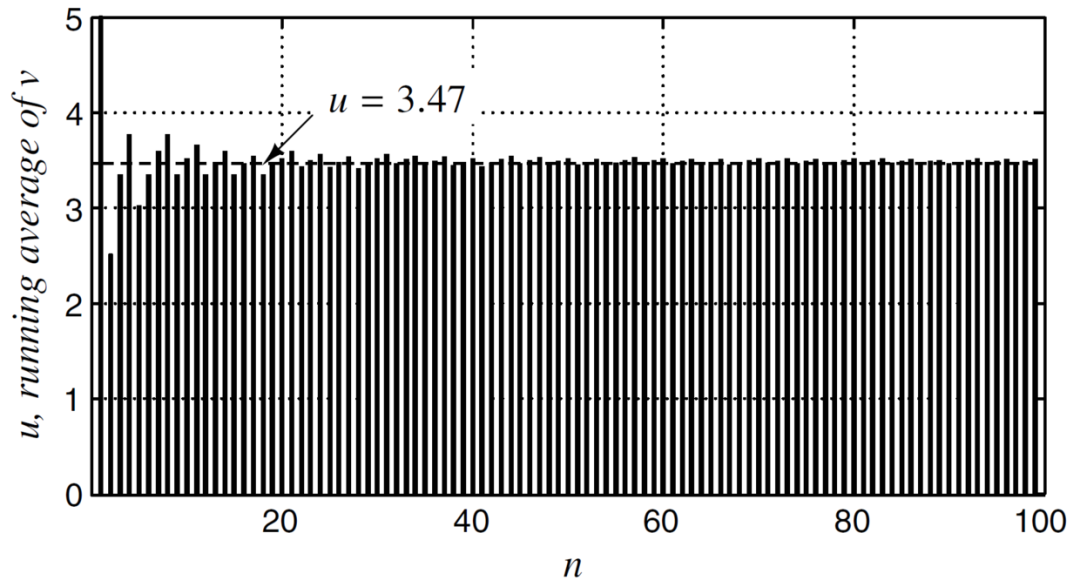
从某种意义上来讲,上述过程类似于一个模数转换的过程。输入的3.47为模拟值,采用二值化的量化输出结果v的长时间平均值来表示输出u,虽然二值化输出结果v并不能代表模拟输入u,但是其长时间均值却可以代表u,这意味着将模拟信号转换成了数字信号。
其它类型ADC的SQNR(Signal-to-Quantization-Noise Ration)取决于量化器的量化间隔,这也符合人们直观的认识,当用一个数字信号表示模拟信号时,自然划分的格子越细,数字信号和模拟信号越接近,意味着实现的精度越高。但是在Σ-Δ ADC中,采用1-bit的量化器就可以实现很高的分辨率,正如前文所提到的,这是一种结构上的完全创新,其包含了以时间换精度的思想。
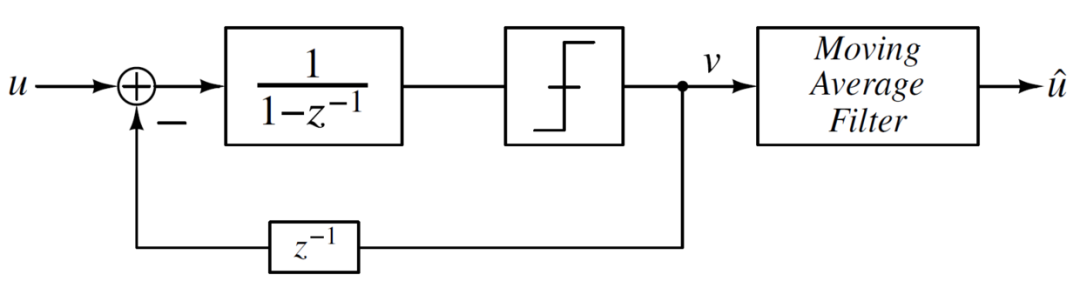
利用信号流图的化简,上述电路结构可以等效成下图所示的结构,这是Σ-Δ ADC更为常用的一种结构,称为误差累积结构,而上述结构称为误差反馈结构。其中1/(1-z ^-1^ )为累加器,这就是Σ的由来,Σ的输入是u和v的差(Δ运算),所以称为Σ-Δ 。该ADC除去输出滤波和降采样部分,称为Σ-Δ调制器,至于为什么叫调制器呢,也许大家第一次接触到的调制的概念就是通信领域的调制解调器,调制是指基带信号对高频载波信号的幅度、频率或者相位进行改变,从而将基带信号的信息加载到了高频载波上。在这里,调制可以认为是对信号处理的一个过程。
对于一个稳定的Σ-Δ ADC,量化器的平均输入为有界信号,这也意味着累加器的平均输入为0,所以u和v的平均值相等。
过采样(Oversampling)
其实,上述情况是假设输入u为一个恒定值,通过环路的迭代才使得v的平均值等于u。如果环路迭代一次,输入u就变化一次,那么就无法实现多次迭代。所以,上述环路的工作速度要远大于输入变化的速度,因此为过采样结构。
从频域上来看,量化噪声在2π范围内平均分布,由于是过采样,所以信号只处于一个非常窄的范围之内,通过滤波操作就极大地减小了量化噪声。这是Σ-Δ ADC利用单比特量化实现了多比特输出效果的一个原因。
过采样本身并不能改善SQNR,而是过采样技术和滤波操作结合才能改善SQNR。

该结构后面的求平均的过程就是上述所提到的滤波器的滤波操作,该数字滤波器后面再接上一个降采样的结构,将高速率的v降到和输入u同样的速率。
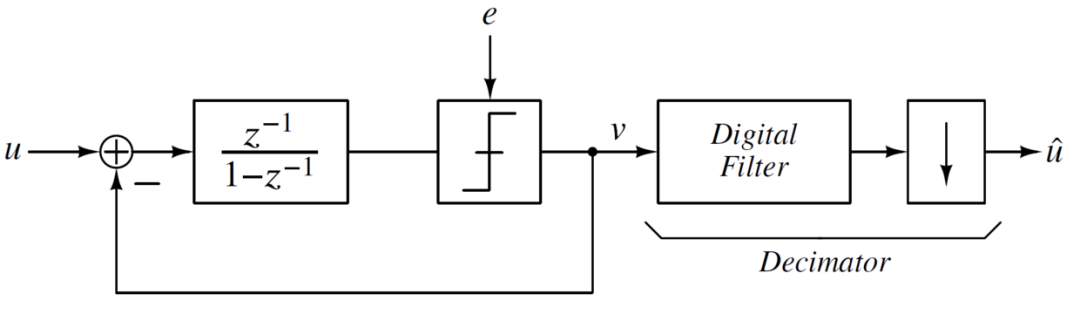
噪声整形(Noise-shaping)
考虑量化器的量化噪声为一个加性白噪声。利用梅森定理,Σ-Δ调制器的量化噪声的闭环输出为:
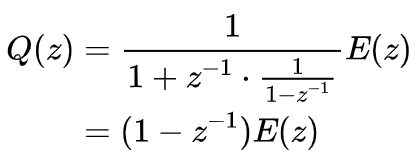
其功率谱密度为:
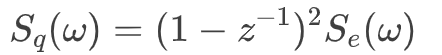
用s变换和z变换的关系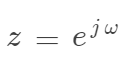 得:
得:
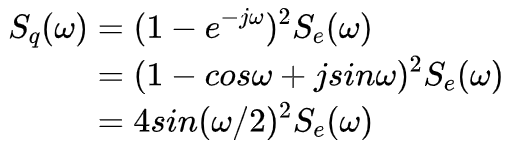
注意这里的ω表示数字角频率,对应于上一篇的Ω的。这里用ω是为了和很多文献保持一致性。
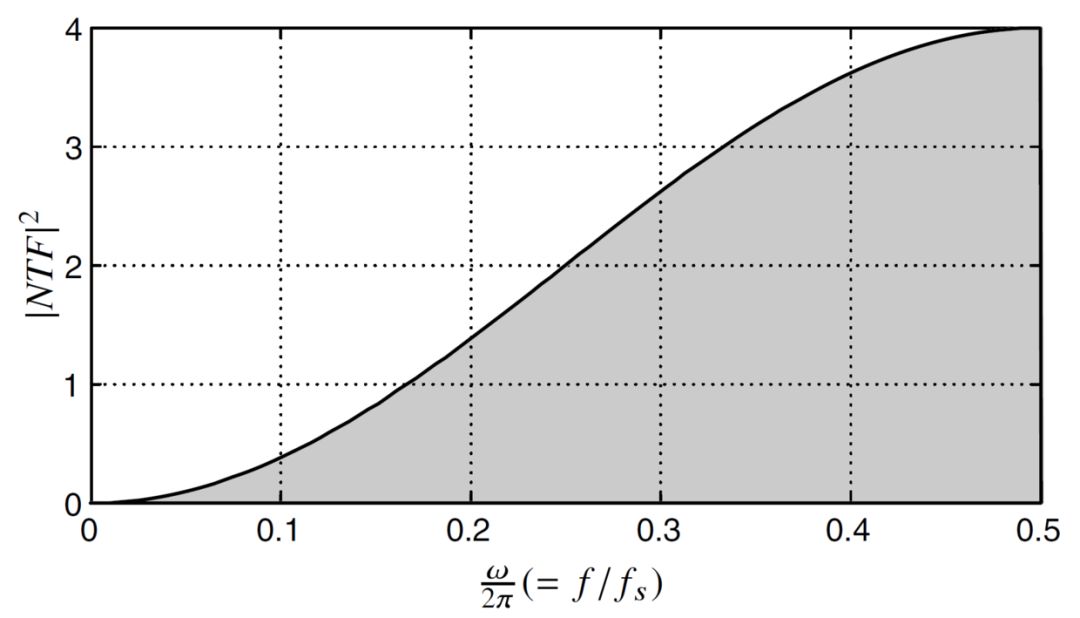
其中,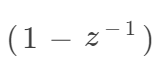 称为噪声传输函数(NTF),其幅度的平方如下图所示,呈现一个高通特性。这使得处于信号带内的噪声被进一步抑制,这是Σ-Δ ADC利用单比特量化实现了多比特输出效果的另一个原因。
称为噪声传输函数(NTF),其幅度的平方如下图所示,呈现一个高通特性。这使得处于信号带内的噪声被进一步抑制,这是Σ-Δ ADC利用单比特量化实现了多比特输出效果的另一个原因。
定义过采样率为:
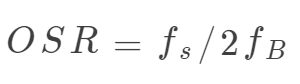 fB为信号的最高频率。
fB为信号的最高频率。
假设量化噪声为白噪声(通常成立),那么带内量化噪声为:
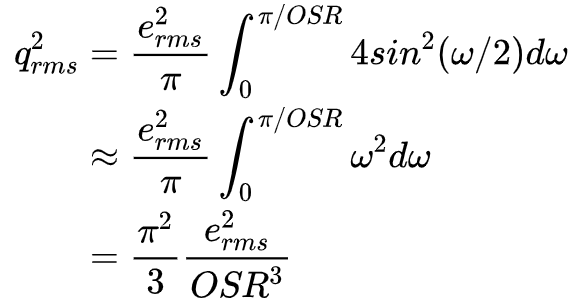
上式可以看出,随着OSR的增加,量化噪声减小。当OSR增加一倍,量化噪声减小9dB,也就是ENOB(effective number of bits)增加1.5bit。#### 二阶Σ-Δ调制器
为了进一步提高分辨率,可以考虑将一阶结构的量化器用一个一阶Σ-Δ调制器替代,如下图所示:
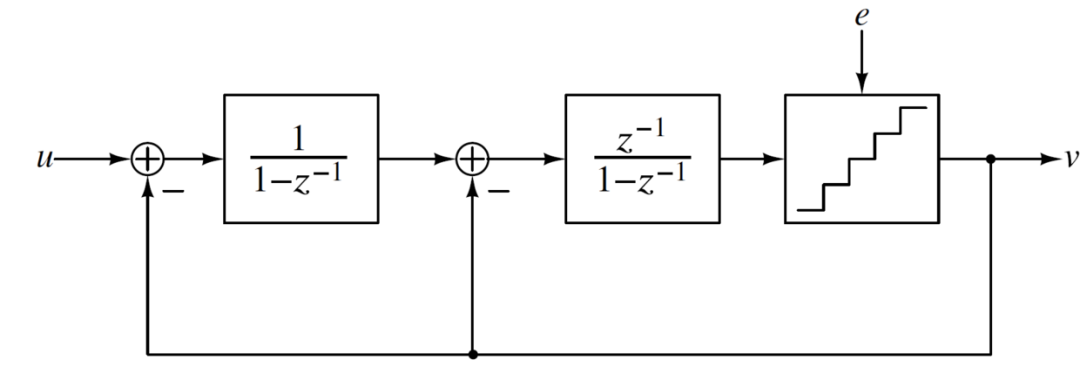 此时,输出V的表达式为:
此时,输出V的表达式为:
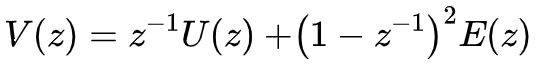
从该式可以看出,现在的噪声整形传函为二阶,应该可以得到更好的噪声整形效果。同理可得此时的带内量化噪声为:
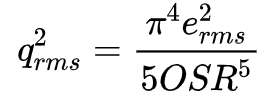
此时,OSR增加一倍,量化噪声减小15dB,也就是ENOB增加2.5bit,表现出更好的噪声整形效果。#### 高阶Σ-Δ调制器
我们可以将上述结构进行推广到L阶,带内噪声功率表达式为:
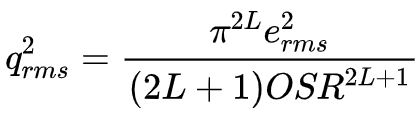
此时,当OSR增加一倍,ENOR增加(L+0.5)bit。那么我们可以一直将阶数增加下去,以至实现一个非常好的SQNR性能的ADC吗?
当然是不可能的,高阶环路会引入稳定性问题,后续文章会介绍这一问题。
多级噪声整形结构(MASH)
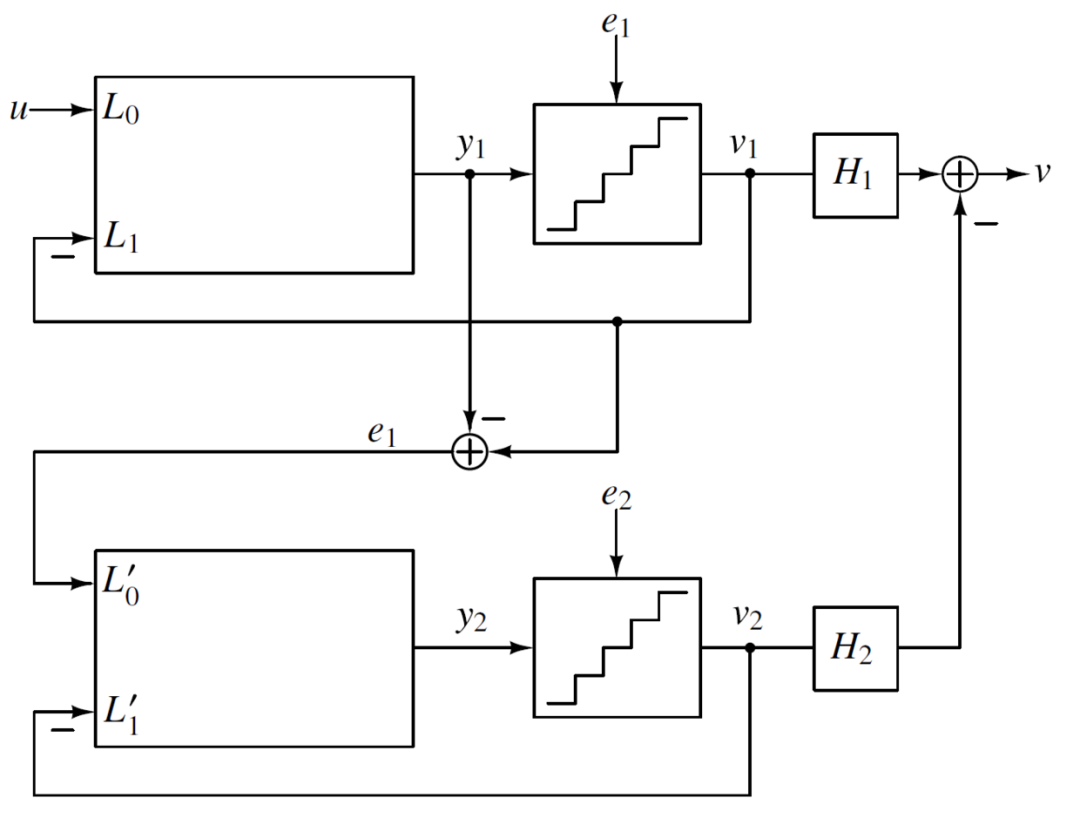
由于多级Σ-Δ结构会有稳定性问题,可以考虑将多个低阶结构进行级联,该结构的稳定性由低阶环路决定,而实现的噪声整形特性却是高阶的。如下图所示,这是一个两级结构级联的MASH结构,将第一级的量化噪声送入到第二级结构的信号输入端,并将两级各自的输出经过一定处理后叠加。如果每一级都是一个两级的Σ-Δ调制器,那么该MASH结构实现了一个四阶噪声整形效果。如下式所示,V1和V2叠加时要将第一级的量化噪声抵消掉:
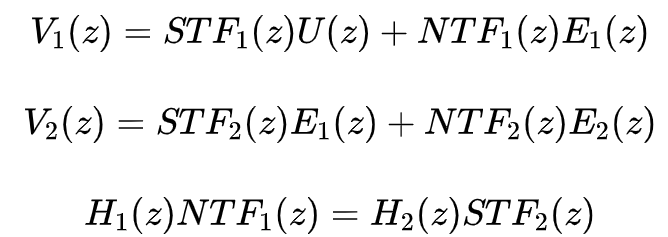
这个结构看似完美,解决了高阶环路的稳定性问题,而又实现了高阶噪声整形效果,但是由于需要实现两式相消,所以它们之间的匹配性成为了很重要一个问题。
多比特Σ-Δ调制器
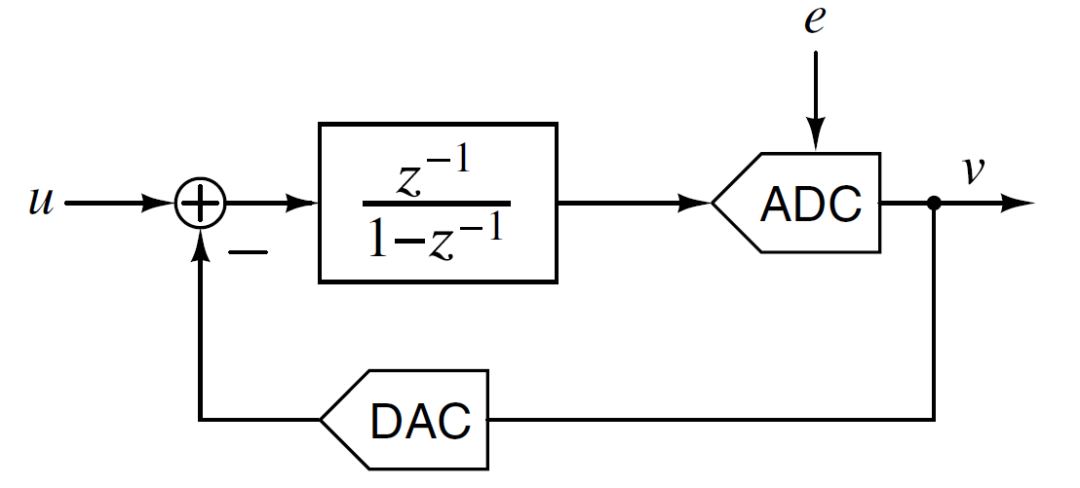
我们将前述的Σ-Δ结构进一步具体化,如下图所示。用一个ADC来表示量化器。之前的结构将量化器输出直接反馈回去和输入的模拟信号相减,我们不可能将模拟信号和数字信号直接进行运算,量化输出结果在反馈到输入端之前首先需要D/A变换。
为什么要引入多比特结构呢?
比特数越多的量化器的量化噪声越小,因此在同样阶数,同样OSR的情况下,可以实现更高的SQNR。
单比特的ADC的增益因子不好确定(后续文章展开),因此在考虑稳定性时,为保证环路增益变化的情况下,环路依然稳定,输入信号幅度需要减小,这降低了SNR。
DAC的非线性会导致调制器输出的非线性。这是由于反馈增益的存在会使DAC的输出等于输入信号u,因此当DAC存在非线性时,DAC的输入便会失真,以使其输出等于输入信号u。
对于一个单比特的DAC,则不存在非线性问题,因为其输出只有两个电平。类似两点确定一条直线的思想,单比特不存在非线性。但是,正如前文所述,量化器采用多比特的ADC具有很大的优势,DAC的位数应该匹配ADC的位数,因此,DAC的非线性还是我们需要解决的一个问题。Trim手段或者Σ-Δ DAC均可以有效解决这个问题。
小结
本文从时域和频域分别阐述了Σ-Δ ADC可以提高SNR的原因,过采样和噪声整形是Σ-Δ ADC的核心思想,理解了它们,意味着我们窥见了其复杂内涵的一角。为了提高其SNR,可以通过提高OSR、环路阶数或者量化器的比特数来实现,但是OSR的提高受限于工作带宽,阶数受限于稳定性,采用高比特的量化器则增加了ADC和DAC的设计难度。此外,还介绍了多级噪声整形技术,它解决了稳定性的问题,却又引入电路匹配的问题。从以上我们可以再次看到模拟电路设计的trade-off,这也正是模拟电路的魅力所在。
-
调制解调器
+关注
关注
3文章
867浏览量
39139 -
SNR
+关注
关注
3文章
197浏览量
24608 -
ADC转换器
+关注
关注
1文章
28浏览量
8390 -
累加器
+关注
关注
0文章
50浏览量
9529 -
射频系统
+关注
关注
0文章
119浏览量
13388
发布评论请先 登录
相关推荐
射频 - 时域与频域的转换
频谱分析仪R3131可以将波形从频域转换到时域吗?
什么是时域和频域?
基于MATLAB的时域和频域抽样计算

从时域、频域讲解OFDMA的原理
深度解析频域和时域的关系

信号分析:搞懂时域与频域的关系





 从时域和频域阐述Σ-Δ ADC提高SNR的原因
从时域和频域阐述Σ-Δ ADC提高SNR的原因











评论