01前言
FPGA实现除法的方法有几种,比如直接用/来进行除法运算,调用IP核进行除法运算,但这两种方式都有个共同的问题——都是黑盒子,在进行时序违例处理时,往往不好操作,比如想打打拍改善下时序都不知从何下手。
02原理介绍
我们都知道商(s)= 分子(FZ)/分母(FM),该计算过程可等效于公式1

其中FM0为FM/2**fm_shift_bit后所得的取值范围为[1,2)数,通过取一个合适的fm_shift_bit的值,使得FM0的值在[1,2]之间。
同理FZ0为FZ/2**fz_shift_bit后所得的取值范围为[1,2)数,通过取一个合适的fz_shift_bit的值,使得FZ0的值在[1,2]之间。
最后经过多次迭代后,由公式1和公式4得,
当FM0*F1*F2*......FN=1时 s=FZ0*F1*F2*......FN*2**(fz_shift_bit-fm_shift_bit)
例子
利用线性迭代的方式计算33/9
步骤如下: 第1步:将分子分母转换为[1,2)之间的数此时得 FZ0 =33/2**5 = 1.03125 FM0=9/2**3 = 1.125 以上部分在FPGA中相当于右移 由公式2、3得到 fm_shift_bit = 3 fz_shift_bit = 5 第2步:利用公式进行线性迭代,令FM0*F1*F2*......FN=FM_PRE,使FM_PRE接近于1 由第1步得FM0=1.125 再通过公式5和公式6得 F1=2-1.125=0.875 FM1=1.125*0.875=0.984375 F2=2-0.9875=1.0125 FM2=0.984375*1.0125=0.9966796875 F3=2-0.9966796875=1.0033203125 迭代 3次后FM_PRE=1.125*0.875*1.0125*1.0033203125 = 0.99998897552490234375接近于1 此时由公式4得: s=1.03125*F1*F2*F3*2**(5-3)= 3.66662624359130859375 与理论计算值误差为4.0423075358072916666666666666667e-6
在实际过程应用中,我们可以根据实际的误差要求确认迭代的次数。
具体的matlab模型代码如下所示
Code
matlab迭代运算代码
function s = div_float(fz, fm, itr ) %----------------------判断结果的符号----------------- if ((fz >= 0) && (fm >= 0)) || ((fz < 0) && (fm < 0)) sign_flag = 0; else sign_flag = 1; end %---------------限定分子范围在[1,2)--------- if fz >=0 fz = fz; else fz = -fz; end fz_shift_bit = 0; if fz ~= 0 fz_inner = fz ; while(fz_inner >= 2 || fz_inner < 1) if fz_inner >= 2 fz_inner = floor(fz_inner/2); fz_shift_bit = fz_shift_bit + 1; else fz_inner = fz_inner * 2; fz_shift_bit = fz_shift_bit - 1; end end fz = fz/2^fz_shift_bit; end %fprintf('a_shift_bit = ');disp(a_shift_bit); %---------------限定分母范围在[1,2)--------- if fm >=0 fm = fm; else fm = -fm; end fm_shift_bit = 0; if fm ~= 0 fm_inner = fm ; while((fm_inner >= 2) || (fm_inner < 1)) if fm_inner >= 2 fm_inner = floor(fm_inner/2); fm_shift_bit = fm_shift_bit + 1; else fm_inner = fm_inner * 2; fm_shift_bit = fm_shift_bit - 1; end end fm = fm/2^fm_shift_bit; end %fprintf('b_shift_bit = ');disp(b_shift_bit); %-----------迭代过程------------------ for cnt = 0:itr-1 f = 2 - fm; fz = fz * f; fm = fm * f; end %------------迭代完成后计算商------------------- %------------当分子分母同时等于0时,令商等于0, %------------否则,当符号标志为正数时,令其等于商的最大值 if fm ~= 0 s = fz * 2^(fz_shift_bit - fm_shift_bit); % fprintf('a = ');disp(a); % fprintf('b = ');disp(b); % fprintf('c = ');disp(c); if sign_flag == 0 s = s; else s = -s; % fprintf('~c = ');disp(c); end else if fz == 0 s = 0; else if sign_flag == 0 s = 256 - 2^-7; else s = -256; end end end
Code
matlab仿真tb
clear;
clc;
close all;
itr = 8;
%-----------定义分子分母和商的精度---------------
delt_fz = 2^-4;
delt_fm = 2^-2;
delt_s = 2^-7;
cntwhole = 1;
for fz = -3232 - delt_fz
for fm = -8 : delt_fm : 8 - delt_fm
s = div_float(fz, fm, itr);
s_real = fz/fm;
if s_real >= 256
s_real = 256 - delt_s;
elseif s_real < -256
s_real = -256;
else
s_real = s_real;
end
err = abs(s_real - s);
s_reg(cntwhole) = s;
s_real_reg(cntwhole) = s_real;
err_reg(cntwhole) = err;
cntwhole = cntwhole + 1;
end
end
figure;plot(s_reg);title("迭代算出的结果");
figure;plot(s_real_reg);title("理论结果");
figure;plot(err_reg);title("误差图");
grid on;
下图迭代参数itr取不同值时的理论值与线性迭代值之间的误差图。
itr=8时
此时最大误差为2.7466*10**-7
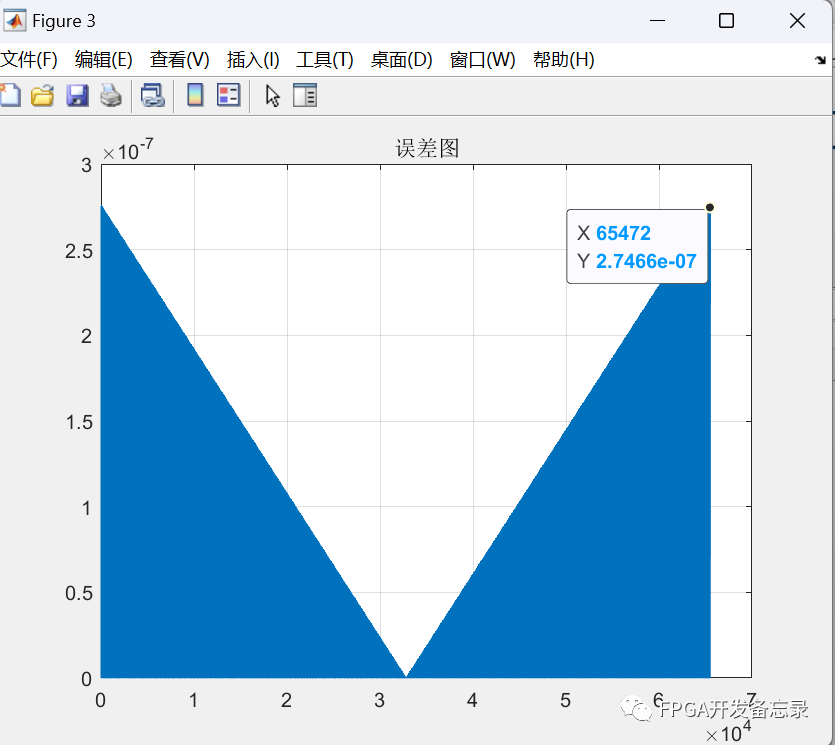
itr=10时
此时最大误差为7.10543*10**-15
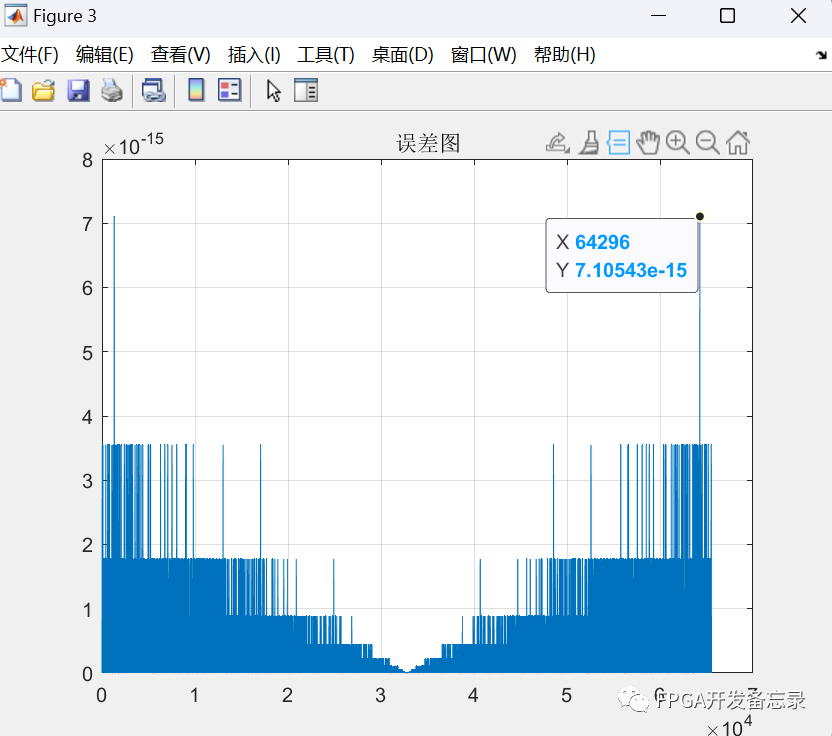
itr=50时
此时最大误差为7.10543*10**-15
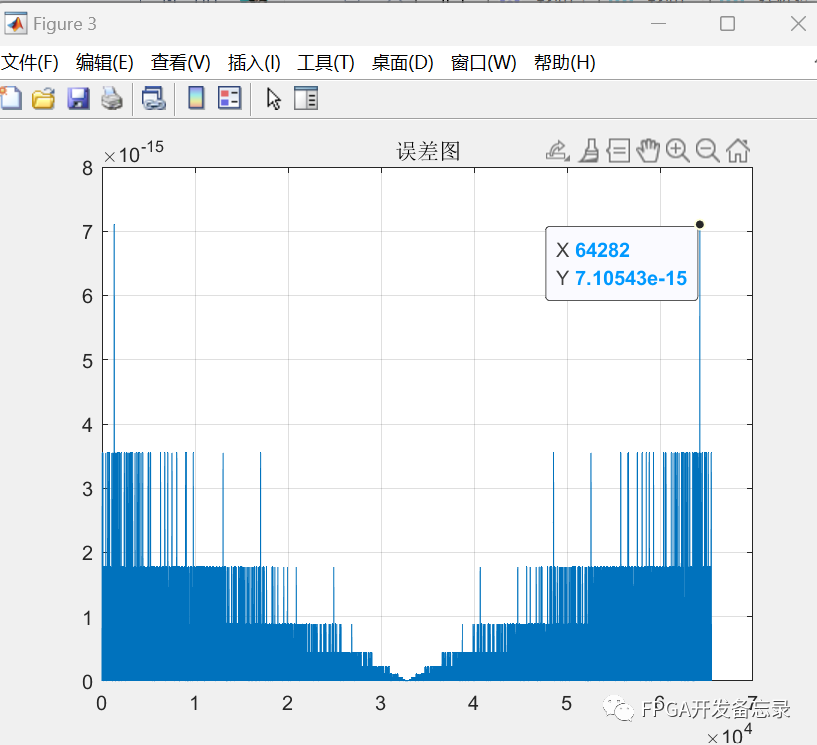
由itr分别取8,10,50后所得到的理论值与线性迭代算出的值做差所得到的误差图可知,并不是迭代次数越多精度越小,当迭代次数达到一个临界值后,迭代的次数其实对商的影响就不是很大了。
-
FPGA
+关注
关注
1635文章
21832浏览量
608132 -
除法器
+关注
关注
2文章
14浏览量
13935 -
时序
+关注
关注
5文章
392浏览量
37519
原文标题:FPGA基于线性迭代法的除法器设计(一)
文章出处:【微信号:Hack电子,微信公众号:Hack电子】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
matlab牛顿迭代法全解
问题:matlab实现牛顿迭代法求解非线性方程
基于牛顿迭代法的FPGA定点小数计算
迭代法迭代阵谱半径新上界
物理光学迭代法计算任意形状开口腔体RCS
用迭代法求指纹图像中的阀值
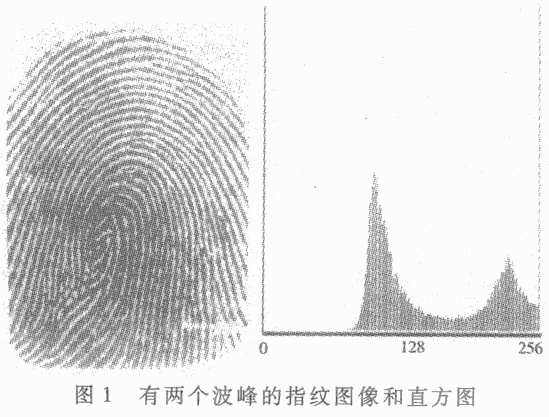
并行除法器 ,并行除法器结构原理是什么?
实例九— 除法器设计





 FPGA基于线性迭代法的除法器设计
FPGA基于线性迭代法的除法器设计










评论