支持向量机（多类问题之1类对另1类）

假设测试样本需被分为三类，首先需构建三个支持向量机模型，分别为：

（1）第一个支持向量机模型将样本分类为类别1和类别2， （2）第二个支持向量机模型将样本分类为类别1和类别3， （3）第三个支持向量机模型将样本分类为类别2和类别3。

然后将每个训练数据输入至上述三个支持向量机的模型中，并采用“投票”的方式确定每个测试样本的类别。例如，对于某一测试样本，若第一个支持向量机模型将该样本分类至类别1，第二个支持向量机模型将该样本分类至类别1，第三个支持向量机模型将该样本分类至类别2，此时，类别1“被投两票”，类别2“被投一票”，类别3“被投零票”，因此，该样本最终被分类为得票数最高的类别1。

但上述“投票”方式可能出现“平票”的情况。例如，对于某一测试样本，若第一个支持向量机模型将该样本分类至类别1，第二个支持向量机模型将该样本分类至类别3，第三个支持向量机模型将该样本分类至类别2。

“平票”情况可导致不能分类问题，1类对另1类的方式可通过将测试样本在上述三个支持向量机模型中各类别的分数加和，并将该样本归类于分数和最大的类别的方式解决上述不能分类的问题。

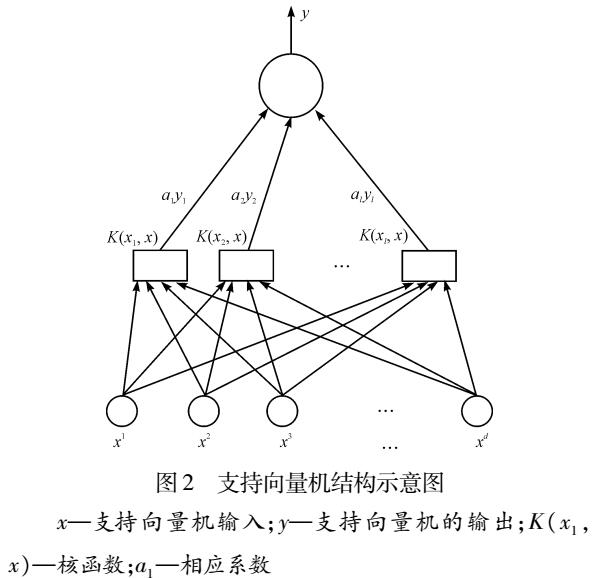
测试样本所获得的分数可通过支持向量机判别式计算得出，即： socre=∑αiyiK(Xi,X)+b 例如，对于某一测试样本，若： 其在第一个支持向量机模型（类别1VS类别2）获得的分数为0.5， 其在第二个支持向量机模型（类别1VS类别3）获得的分数为-0.2， 其在第三个支持向量机模型（类别2VS类别3）获得的分数为0.4。

则该样本在上述三个支持向量机模型中： 对类别1的分数和为0.5-0.2=0.3， 对类别2的分数和为-0.5+0.4=-0.1， 对类别3的分数和为0.2-0.4=-0.2。 即该样本对类别1的分数最大，因此该样本被归类于类别1。

1类对另1类的方式可解决机器学习相关介绍（20）——支持向量机（多类问题之1类对K-1类方式）中1类对K-1类方式训练样本不平衡的问题，但1类对另1类方法需训练的支持向量机的数量为K(K-1)/2（K为类别数），当K较大时，训练和测试时间较长。

因此，支持向量机可综合1类对K-1类和1类对另1类的方式，得出如图一所示的树状方式（下文简称“树状方式”）。该树状方式处理的是一个8分类问题，在处理该问题时，需构建7个分类器（支持向量机模型），每个分类器区分两个类别。



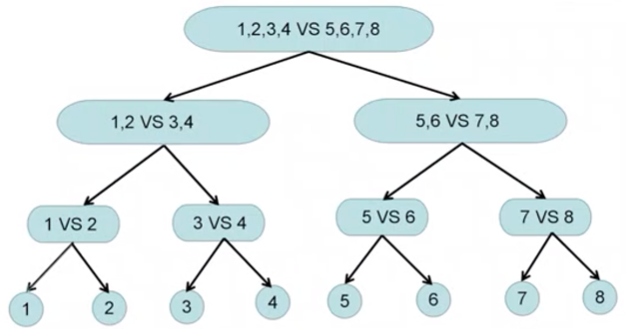
图一，图片来源：中国慕课大学《机器学习概论》

该树状方式在减少分类器数量的同时兼顾了类别样本数量的平衡。该树状方式需保证每个分类器所区分的两类差别是显著的，例如“1、2、3、4VS5、6、7、8”两类的差别是显著的。






审核编辑：刘清