Smith圆图是什么？Smith圆以及阻抗匹配介绍

  Smith圆图是什么？

  是由菲利普·史密斯(Phillip Smith)于1939年发明的，由很多圆周交织在一起的一个图，是反射系数的极坐标图。史密斯曾经说过：“在我能够使用计算尺的时候，我对以图标方式来表达数学上的关联很有兴趣。”

  Smith圆图常用于协助解决传输线问题和阻抗匹配问题。本文将为大家介绍使用方法。

  一、相关参数

  1、反射系数

  信号沿传输线向前传播时，每时每刻都会感受到一个瞬态阻抗，这个阻抗可能是传输线本身的，也可能是中途或末端其他元件的。对于信号来说，它不会区分到底是什么，信号所感受到的只有阻抗。如果信号感受到的阻抗是恒定的，那么他就会正常向前传播，只要感受到的阻抗发生变化，不论是什么引起的（可能是中途遇到的电阻，电容，电感，过孔，PCB转角，接插件），信号都会发生反射。

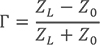
  归一化负载阻抗：

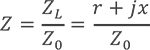
  得到：

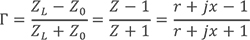
  当中的Γ代表其线路的反射系数(reflection coefficient)Z是归一负载值，即ZL/ Z0。当中，ZL是线路本身的负载值，Z0是传输线的特征阻抗（本征阻抗）值，通常会使用50Ω。

  2、驻波比

  驻波比全称为电压驻波比，又名VSWR和SWR，为英文Voltage Standing Wave Ratio的简写。指驻波波腹电压与波谷电压幅度之比，又称为驻波系数、驻波比。驻波比等于1时，表示馈线和天线的阻抗完全匹配，此时高频能量全部被天线辐射出去，没有能量的反射损耗；驻波比为无穷大时，表示全反射，能量完全没有辐射出去。

  驻波比可以通过反射系数来计算得出：

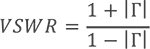
  3、S11

  S11实际上就是反射系数Г，只不过它特指一个网络1号端口的反射系数。反射系数描述的是入射电压和反射电压之间的比值，而回波损耗是从功率的角度来看待问题。RL=-S11。

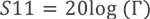
  4、阻抗

  在具有电阻、电感和电容的电路里，对电路中的电流所起的阻碍作用叫做阻抗。阻抗常用Z表示，是一个复数，实部称为电阻，虚部称为电抗，其中电容在电路中对交流电所起的阻碍作用称为容抗,电感在电路中对交流电所起的阻碍作用称为感抗，电容和电感在电路中对交流电引起的阻碍作用总称为电抗。阻抗的单位是欧姆。

  电阻：

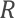
  电容：

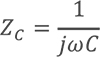
  电感：

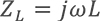
  阻抗：

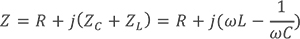
  因为电容和电感的存在，它会是一个复数。

  （1）如果(ωL–1/ωC) > 0，称为“感性负载”；

  （2）反之，如果(ωL–1/ωC)<0，称为“容性负载”；

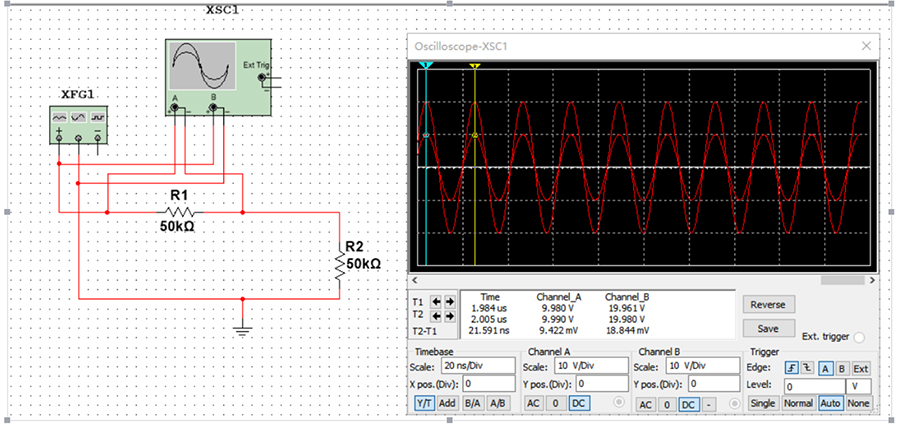
  如果电路中只有电阻，它只会影响信号的幅度，如下图所示：

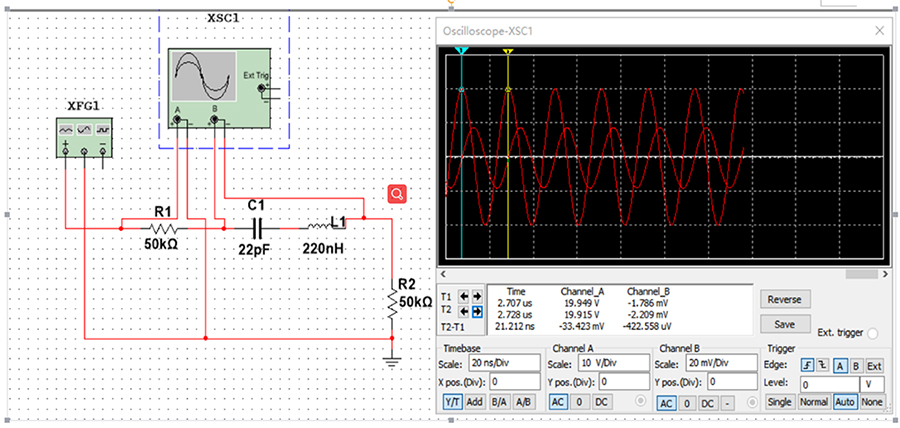
  如果电路中不仅存在电阻，还存在电感及电容时，不仅会影响信号幅度，同时相位、频率特性也会发生变化，所以计算过程中即需要考虑实部，也需要考虑虚部。如下图所示：

  二、如何记住Smith圆

  我们可以在一个复平面里面，以实部为x轴、以虚部为y轴，表示任意一个复数。我们的阻抗，不管多少电阻、电容、电感串联、并联，之后，都可以表示在一个复平面里面。

  在RLC 串联电路中，交流电源电压U = 220 V，频率f = 50 Hz，R = 30 Ω，L =445 mH，C =32 mF。

  综上可得：

  X（L）=2πfL≈140Ω

  X（C）=1/2πfC≈100Ω

  则：

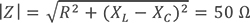
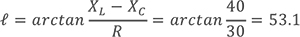
  在复平面中表示：

  各种阻抗的情况，组成了这个无穷大的平面。

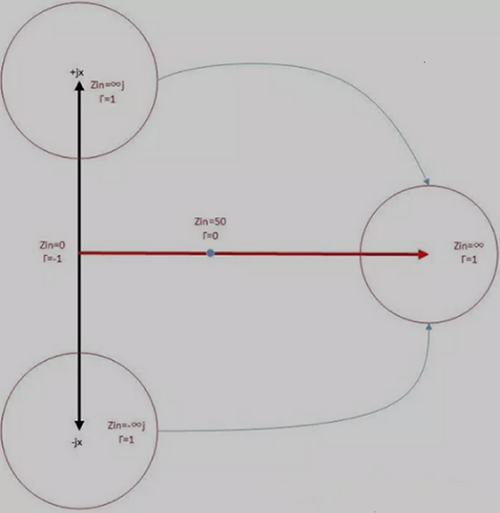
  下面就开始方便我们去记住Smith圆图，我们将进行"变身“：

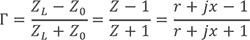
  将复平面图，进行扭曲变成圆，变身过程如下：

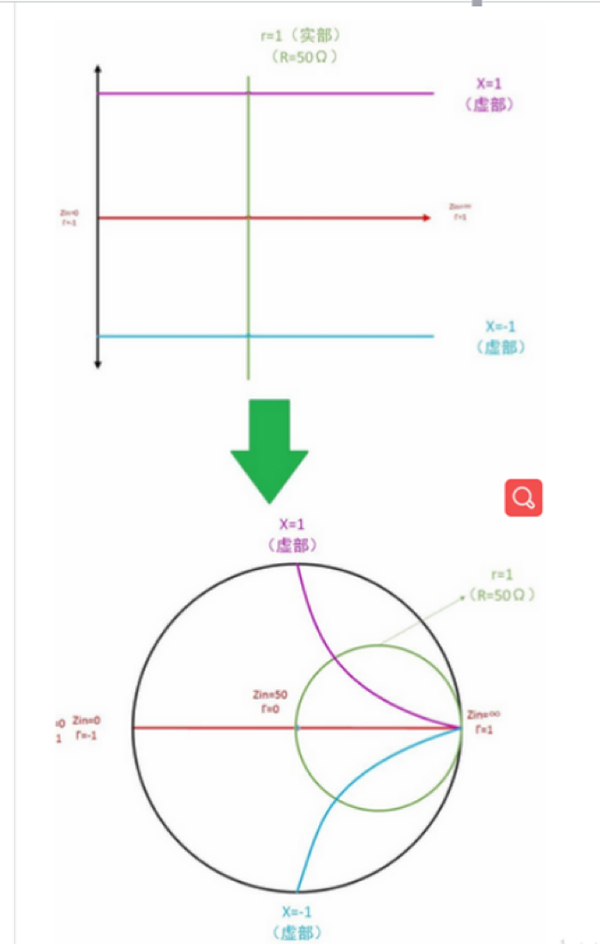
  红色的线上的阻抗，有个特点：虚部为0；（电感、电容为0）

  紫色的线上的阻抗，有个特点：虚部为-1；

  蓝色的线上的阻抗，有个特点：虚部为1；

  三、Smith圆图操作

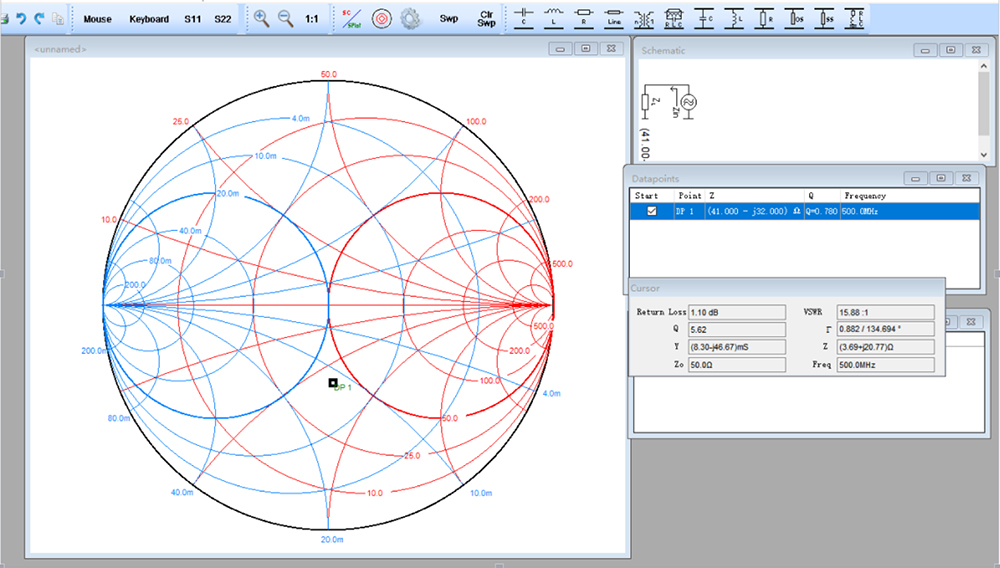
  红色是阻抗图，绿色是导纳图；

  上半圆表示感性负载，下半圆表示容性负载，中间红线表示纯电阻；

  串联器件看阻抗图：

  （1）串联电感顺时针移（增加感性）

  （2）串联电容逆时针移（增加容性）

  并联器件看导纳图:

  （1）并联电感逆时针移（增加感性）

  （2）并联电容顺时针移（增加容性）

  总之，都是往增加该器件属性的方向移动；

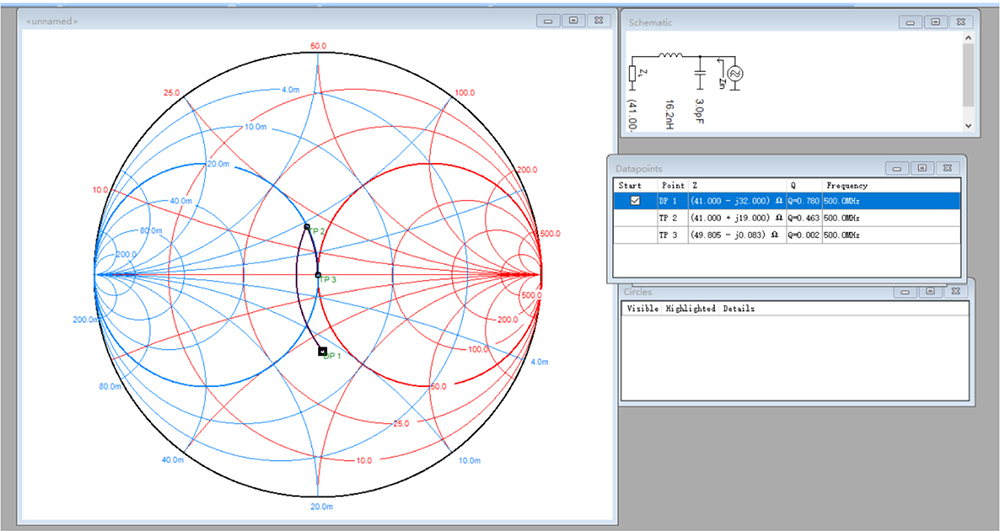
  比如上图P1点需要往中心点靠，可以先阻抗图顺时针转，再导纳图顺时针转，即通过串电感，再并电容。如下图，串联16.2nH电感到P2点，再并联3.0pF电容到P3点。

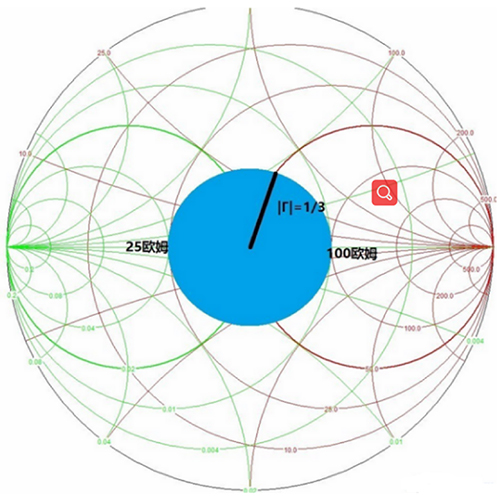
  平时做阻抗匹配时不可能完全做到匹配后反射系数为0，通常希望反射系数绝对值小于1/3(这时对应RL≈-10dB，VSWR≈2，反射率≈11%)，即下图蓝色区域。

  正确的使用Smith圆图，可以在不作任何计算的前提下得到一个表面上看非常复杂的系统的匹配阻抗，唯一需要作的就是沿着圆周线读取并跟踪数据。