简 述 :****
SPWM正弦脉宽度调变技术原理为由控制器产生的三相正弦波电压命令与三角波做比较,经过比较器,产生脉宽调变讯号驱动逆变器,并使其输出近似正弦波且为等幅不等宽的电压波形。根据正弦波电压和三角波的大小和频率,可定义为下列两个指标,其一为调变指标 (Modulaton Index)为:
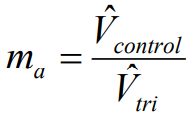
式中Vcontrol为三相正弦波电压峰值大小,Vtri为三角波峰值的大小。
其二为频率调变比(Frequency modulation ratio),定义为:
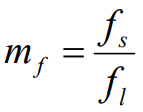
式中fs为三角波频率,f1为正弦波电压频率。
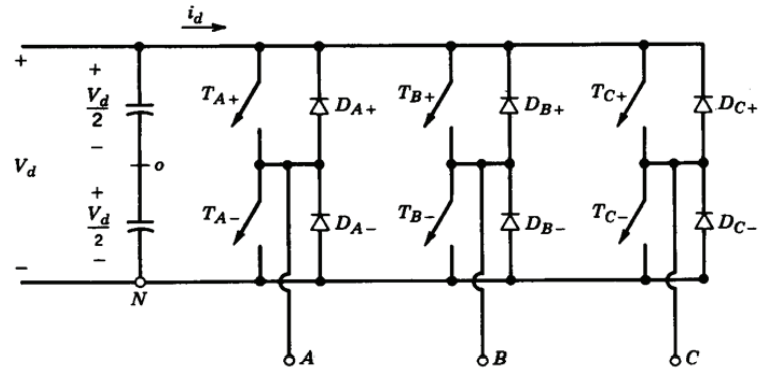
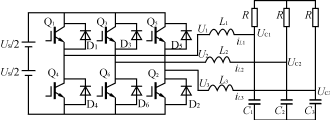
上图为三相逆变器电路图
三相SPWM :****
以A相为例,电压VAN其基本波的峰值可用下式表示:
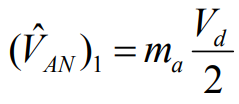
基本波线-线电压大小(RMS)为:
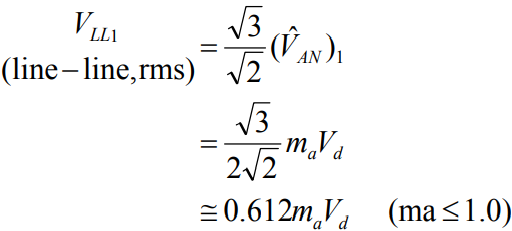
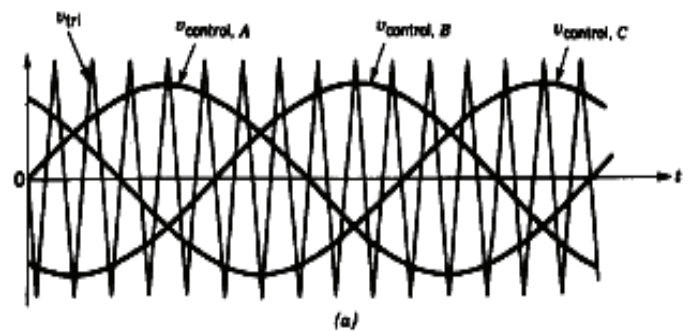
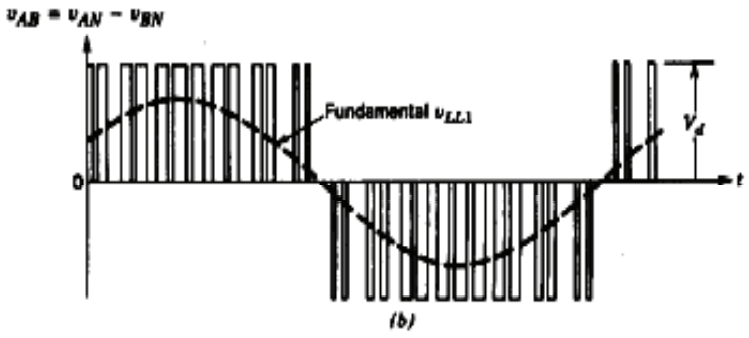
当ma≤1时,称为逆变器的线性调变区,亦即当输入正弦波电压命令的峰值比三角波峰值小时,输入电压大小会与逆变器输出电压基本波的线-线电压大小成正比。其三角波与正弦波如下图所示:

三相空间向量SVPWM:
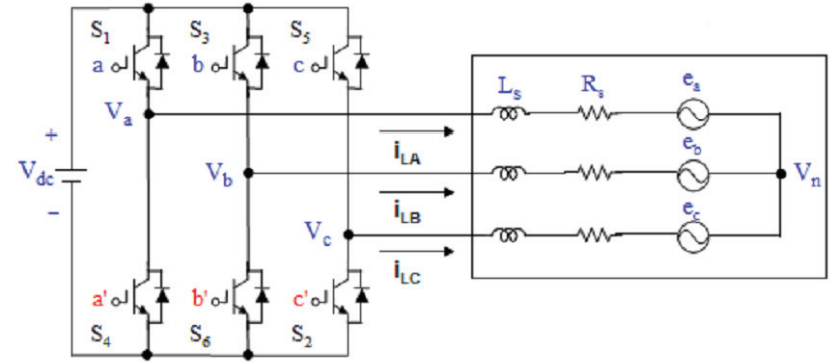
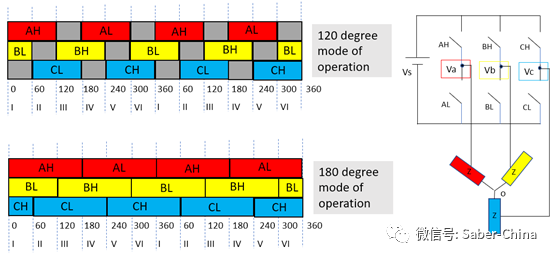
空间向量脉宽调变即是利用电压空间向量的观念,即由逆变器之六个功率组件的开关切换状态来产生旋转的电压向量空间,典型的三相变频器如图所示,其每相各有两个开关组件置于上臂及下臂,分别为上臂的S1、S3、S5及下臂的S2、S4、S6。在空间向量脉宽调变的控制模式下,逆变器每相开关组件的导通状态为互补式,即代表若上臂导通则下臂截止,反之若上臂截止则下臂导通。在控制上通常在开关导通前加入一延迟时间以避免上臂与下臂功率组 件同时导通造成功率组件的损坏,此一延迟时间称之为死区时间。在此定义开关导通状态a、b、c相每一臂之开关导通状态,若a=1则代表上臂开关导通下臂开关截止,a = 0则代表上臂开关截止下臂开关导通。因此三相逆变器之输出状态共有八种,每一种状态产生的线对线电压,相电压之输出结果(直流链电压为VDC)列于下表。
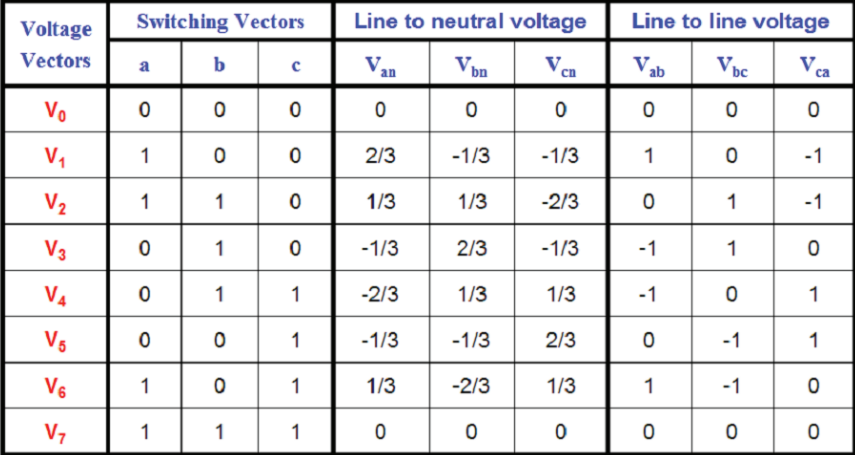
由上表可以得知,三相逆变器输出之相电压和线间电压之关系,经由坐标轴转换至αβ平面上可得下表,其转换之关系式为:
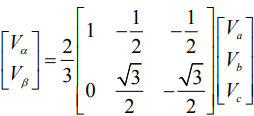
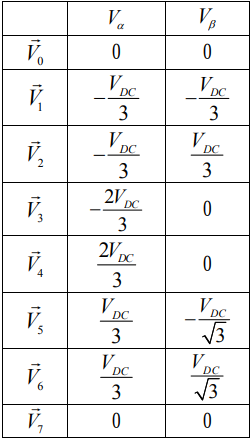
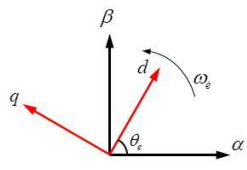
因此即由此八种开关切换状态将可得到八种不同的电压向量。此八个电压向量称为基本电压向量,分别为六个有效电压向量V1、V2、V3、V4、V5、V6及两个零向量V0及V7。因此可利用此六个有效电压向量将电压空间平面分为六个区间,如下图所示。其中αβ平面之α轴及β轴乃相对于交流马达定子之水平轴及垂直轴, Vref则为输出之参考电压向量。
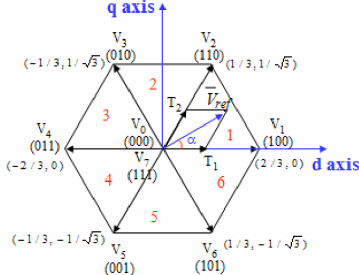
任何大小之输出之参考电压Vref可以用图中六个有效电压向量中之任两个向量表示,而此输出电压在这两个有效电压向量之分量(导通时间)可用代数方法求得。
轴转换:
静止坐标轴转换:
将三相abc静止坐标轴转换至αβ静止坐标轴系统,此转换称为Clark转换。依据下图所示两个坐标系统之间的关系,得出如下式的坐标转换式:
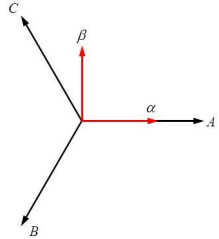
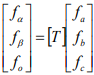
fa、fb、fo为电压及电流等在αβ轴下的变数量
fa、fb、fc为电压及电流等在abc轴下的变数量
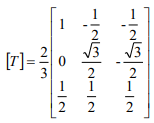
反之,将坐标轴αβ转换至三相abc坐标系统,此转换称为反Clark转换,转换公式可表示:
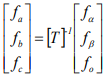
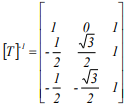
以上为由三相abc坐标系统与静止坐标系统之间关系式,其转换矩阵前的未定系数,若是采用非功率不变法则此为3/2,
若是采用功率不变法则此为
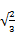
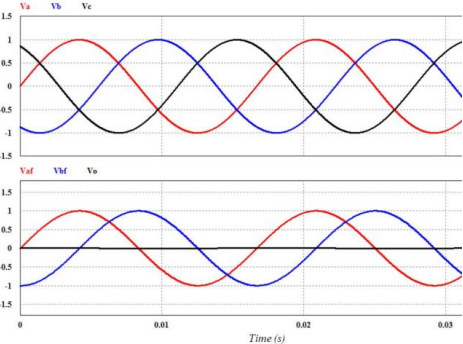
本文是采用非功率不变法则。此外,对于三相平衡系统,因此在做静止坐标轴转换时,零序分量是可被忽略的。下图是采用PSIM仿真abc静止坐标轴转换至αβ静止坐标轴之波形图。
同步旋转坐标轴转换:
前一节透过坐标轴转换将abc静止坐标系统转换至ab静止坐标轴系统,本节进一步将αβ静止坐标轴转换至DQ同步旋转坐标轴系统,此转换称为Park转换,此时假设三相系统为平衡,零轴分量可被忽略,并将DQ轴与αβ轴同时放在二维向量平面上,如图3.7 所示,此旋转坐标以ωe角速度来旋转,故可得坐标转换公式:
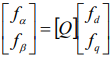
其中:
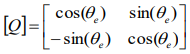
反之,将旋转坐标系统DQ轴转换至ab坐标系统,此转换称为反Park转换,则转换公式可表示:
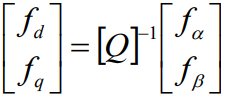
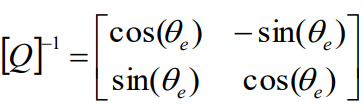
实验验证:
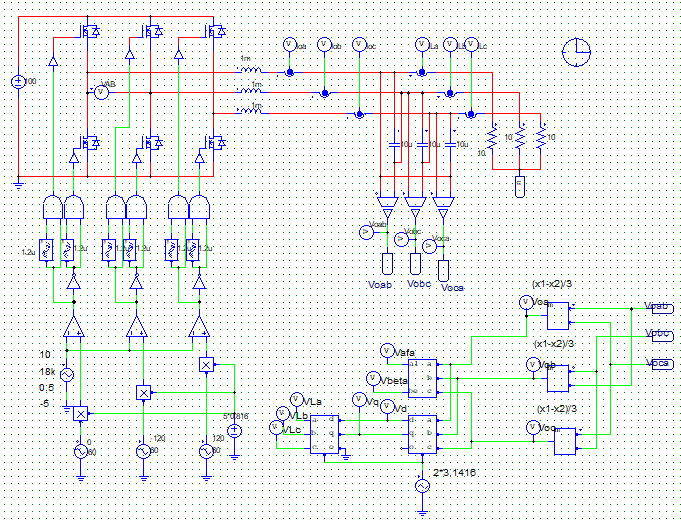
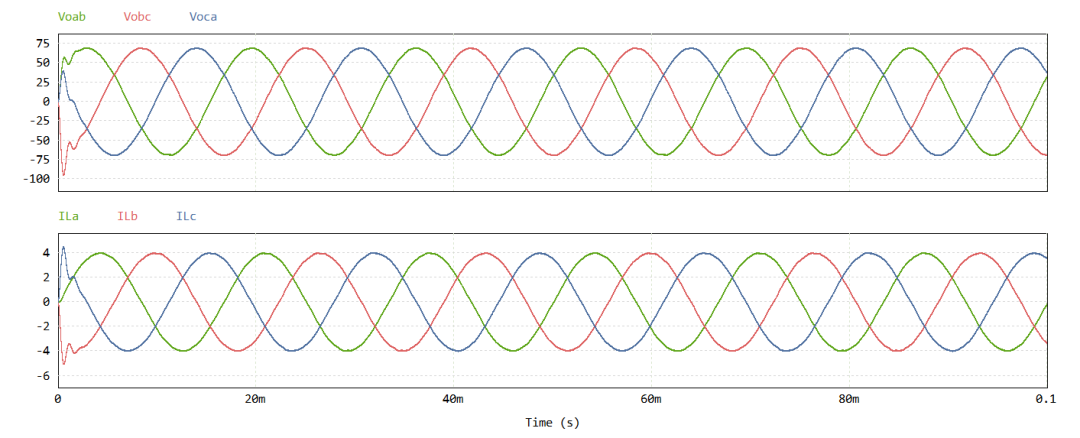
-
转换器
+关注
关注
27文章
8778浏览量
148716 -
控制器
+关注
关注
113文章
16562浏览量
180303 -
变频器
+关注
关注
252文章
6624浏览量
146577 -
SPWM控制
+关注
关注
0文章
22浏览量
8616 -
三相正弦波逆变器
+关注
关注
0文章
2浏览量
1377
发布评论请先 登录
相关推荐
降低三相IGBT逆变器设计系统成本的方法
如何利用三相逆变器控制电机
谐振逆变器三相电路的原理是什么
三相SPWM逆变电路的设计
基于fpga的三相逆变器系统设计
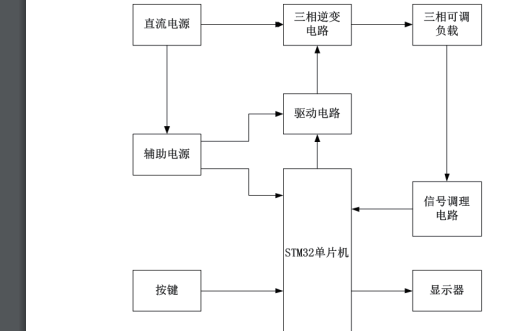
如何使用STM32单片机进行三相逆变器的设计




 PEK-130模块之三相正弦脉宽调变逆变器设计
PEK-130模块之三相正弦脉宽调变逆变器设计











评论