数据处理中最重要的滤波原理讲解

我们知道，滤波器通常用于降低噪声并提高数据质量。

注意这个滤，指的是衰减而非一刀切~

但是在滤波的过程中会出现各种问题，这些问题有的会对最终结果产生极大的影响，导致我们的结果很难解释清楚。

脑科学的主要挑战之一是在测量时会存在噪声和伪迹污染。

这些可能包括环境噪声，仪器噪声或由体内信号源产生的噪声，很明显，我们对这些干扰信号不感兴趣。

举个最简单的例子，如果信号和干扰占据不同的频段，那么我们可以通过对数据应用滤波器来改善信噪比（SNR），也就是将干扰衰减至最低，同时保证有用信号完美通过。

而滤波，也就是对信号进行不同程度地衰减，也可以理解为对信号的放大倍率进行处理，一个意思。

接下来，我们来看一看从数据记录到最终展示出来，都在哪里应用到了滤波：

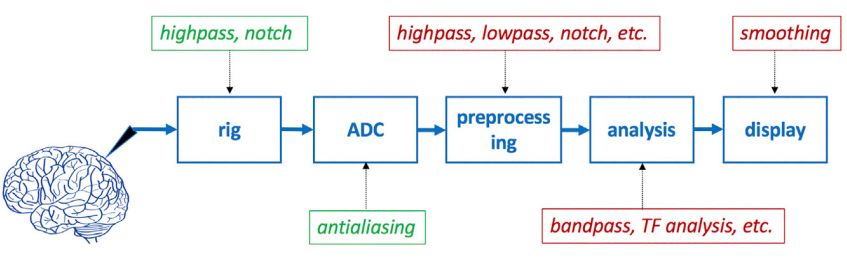
共5处，绿色框处为模拟滤波，红色框处为数字滤波。

我们最开始采集到的大脑数据是连续的模拟信号，为了转换成我们处理起来更方便的离散的数字信号，就会用到 ADC （模拟-数字转换器）。对于现代信号处理来说，这种处理已经从模拟领域逐渐转至数字领域了。

① 测量装置或放大器

可能包括 高通滤波器和陷波滤波器 ，而像脑电这类记录细胞外脑活动的测量装置的放大器通常是交流耦合的，所以这里可以省略高通。

PS：这里可能会涉及一些耦合电容等电路上的概念，就不展开讲了，有兴趣的读者可自行百度~

② ADC

就是模数转换，但在 AD转换 （模-数转换）之前，会有一个低通抗混叠滤波器。这个抗混叠滤波器的作用是：滤除奈奎斯特频率以上的频率分量。

这里单独讲一讲：当今的数据处理几乎都是在数字领域进行的，这就要求信号在时间上进行离散采样。而在采样过程中只保留采样点的值，因此此时的信号是模糊的。

如果这种采样信号满足一定的条件，那么就可以完美重建原始信号，这里引入 奈奎斯特采样定理 ：采样频率要大于两倍信号所包含的最高频率；

但在真正应用时，我们一般都会取最高频的3~5倍或更高，来作为采样频率。这个采样频率的一半，就称作奈奎斯特频率，或奈奎斯特极限，这个极限是完美重构原始信号的关键。

而如果在采样时，奈奎斯特频率以上还存在更高的频率分量，那么我们还原后的数字信号就会产生失真（混叠），混叠是指采样信号被还原成连续信号时产生彼此重叠而失真的现象，在理想滤波的情形下，滤掉高于奈氏频率的信号成分即可防止混叠。

为了保证我们可以完美重建信号，我们需要将奈氏频率以上的频率分量全部滤除。抗混叠滤波就是做这个的。

③ 预处理

包括低通、高通、陷波等等，视需求而定。

低通 ：一般用于滤除高频分量和消除毛刺。

高通 ：一般用于消除直流（DC）分量和缓慢漂移电位的影响。

陷波 ：一般用于消除市电干扰（50、60Hz）。

但除了50Hz这种电源工频干扰，还存在由其产生的整数倍的谐波干扰（100、150Hz等），文献的作者提出：可以应用boxcar smoothing kernel of size 1/50 Hz来解决。

PS:这个我也没有见过，百度了一下好像是一种加矩形窗的函数，效果就是在电源的各个谐波上都有零点，从而真正消除电源干扰。

④ 数据分析

可能涉及带通滤波（例如，隔离标准频段，如'alpha''或''gamma''）或TF分析。

⑤ 展示

可能需要额外的平滑（也就是低通滤波），以去除毛刺/锯齿。、

PS：这里我们先大致按以下方式理解一下低频和高频：低频代表了整个信号的缓慢的变化趋势，高频代表了信号局部的剧烈变化。

好，我们接着往下讲：

通俗来说，滤波器就是修改输入信号的频谱内容的东西。

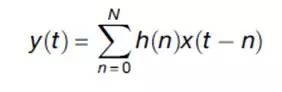
对于数字滤波器来说：t是分析时间点，h（n）（n = 0，....，N）是冲激响应，上面这个方程就是卷积（也可以按滑动平均来理解）。

冲激响应 (Impulseresponse，或者叫脉冲响应)就是某个线性时不变系统的输入输出关系的基本特征，它是由系统本身的性质决定的，也就是在这个滤波器一出生时就定好了的！

冲激响应这个概念比较重要，需要大家理解，以方便之后理解卷积。

线性时不变：线性和时不变，都是针对一个系统说的，这个系统可以是滤波器，也可以是别的等等。

①线性：指系统满足叠加性和齐次性，叠加性指：当多个输入作用于系统时，系统的输出等于单个输入的作用之和；

②齐次就是输入放大n倍，输出也放大n倍。

卷积 ：输出 = 输入 * 系统(输入与系统的冲激响应做卷积，得到系统的输出)，同样，这个系统可以是滤波器，也可以是别的什么东西。任一个线性系统的输出都可以通过将输入信号与系统函数（系统的冲激响应）做卷积获得。

或者可以这么理解，

卷积是某一时刻的输出是之前很多次输入乘以各自的衰减系数之后的叠加而形成的，然后再把不同时刻的输出点放在一起，形成一个函数，这个函数就是输出的函数。

在讲述下面这张图之前，先明确一个概念：因果性。

我们说，如果这个系统当前时间点的输出仅仅与当前时间点及之前时间点的输入有关，那么我们说这个系统是因果的；反之，如果这个系统当前时间点的输出还与之后时间点的输入有关，那么我们说这个系统是非因果的。

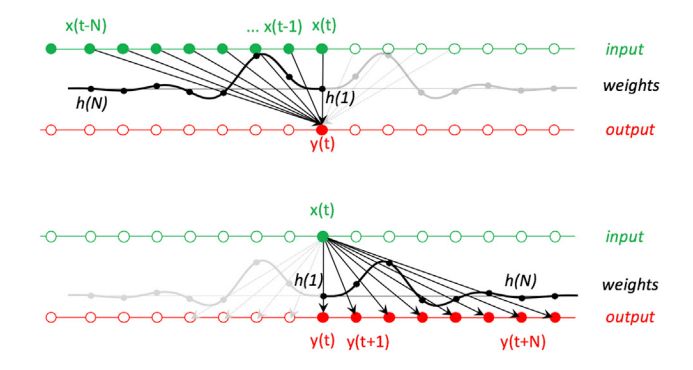
结合这张图来理解卷积。这张图基于的是因果系统：绿线为输入信号，它的时间序列是离散的；灰线为系统的冲激响应，是这个系统自身的特性；红线为输出。

上下两部分讲的是一个东西。咱们以上面的为例：输出y的每个瞬时值是由冲激响应h(n)加权后的输入x的瞬时值之和。对于因果滤波器，仅输入的过去或现在的瞬时值作出贡献（对应到h(n)的黑色部分）。对于非因果过滤器，未来的样本也可以贡献（对应到h(n)的灰色部分）。

如果没有理解，那么再来看下图：描述卷积过程的另一种方式是输入x的每个瞬时值影响输出y的多个瞬时值，其影响的权重由冲激响应h(n)确定。

而按照n的有限长或是无限长，我们又可将滤波器分为 FIR和IIR 。

**IIR（无限冲激响应）**由于其无限长的冲激响应，导致其幅频特性精度很高，但其相位是非线性的，可以应用于对相位信息不敏感的信号上；

**FIR（有限冲激响应）**的幅频特性精度较之于IIR低，但是相位是线性的，所以不同频率分量的信号经过FIR滤波器后不发生相移。

我们再来说说滤波器的性能：性能取决于过渡带的陡度，过渡带的陡度取决于滤波器的类型和阶数。过渡带可以大致理解为：通带与阻带间的部分。

下图为四种常见类型的滤波器：低通，高通，带通和陷波。

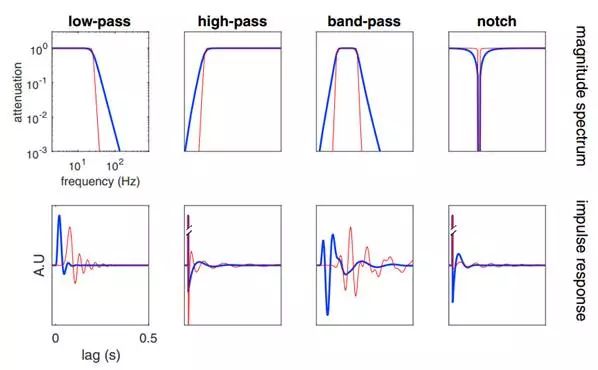
上半部分是幅度谱，下半部分是每个滤波器的冲激响应。

对于每个滤波器，显示了两个版本，前三个的蓝色为4阶巴特沃斯滤波器，红色为16阶。第四个蓝色为Q因子（中心频率与带宽的比率）为1(红为10）的二阶滤波器。

我们可以看到：阶数越高，性能越好。同时在频域中过渡带越陡，在时域中冲激响应越宽（时域扩展-频域压缩）。

了解了以上这些，我们来看看滤波器是如何影响大脑数据的。

以下，我们将回顾在大脑活动的时间序列中可能出现的一些典型“事件”，并了解它们如何受到常用滤波器的影响。

这个问题的答案取决于数据和滤波器。

1.脉冲或尖峰

在大脑的短暂的局部活动中，其神经元的“尖峰”活动可以被建模为一个或几个脉冲。

下图为：滤波对短暂的局部事件（脉冲或尖峰）的影响。

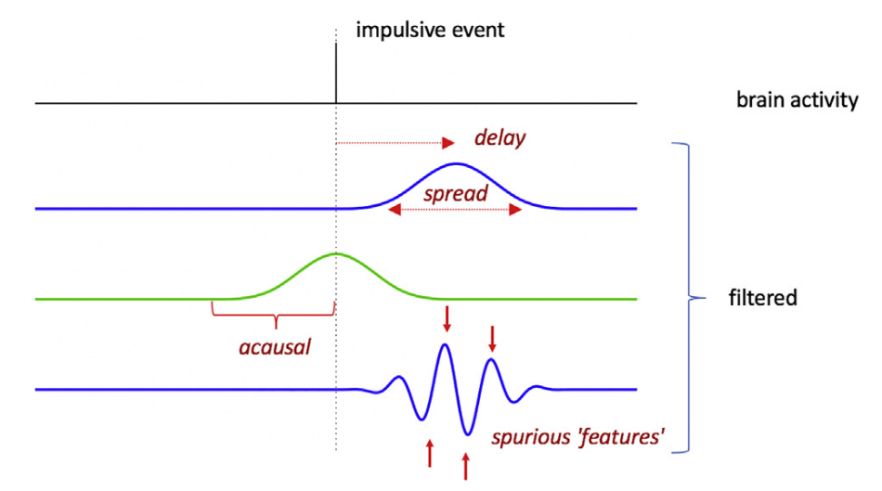
系统的响应(输入称为激励，输出是响应)随时间扩展（即，不再精确地在时间上定位）并且如果滤波器是因果关系则输出会有延迟。如果滤波器是零相位（绿色），则消除整体延迟，但响应是非因果的（即绿线所示）。

这种响应可能包括由于滤波器振铃效应引起的多个伪特征。

什么是振铃效应？

振铃效应 ，原指在图像处理中，对一幅图像进行滤波处理时，若选用的频域滤波器具有陡峭的变化，则会使滤波图像产生“振铃”。

我们以理想低通滤波为例，其在时域上的表现为sinc函数，对于辛格函数sinc而言，经过傅里叶变换之后的函数形式为窗函数（理想低通滤波器在频域上的形状）形式，用图像表示如下：

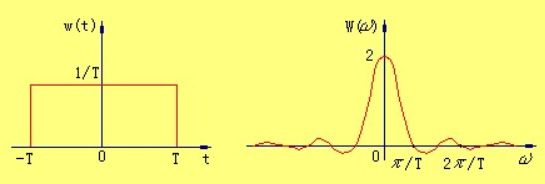
滤波，就是将系统与输入在频域相乘，转换到在时域上就是卷积，由于受到sinc两边余波的影响，导致图像出现振铃现象（这里要理解卷积的概念，才能更好地理解振铃现象）。

上述影响的性质取决于滤波器，可以通过观察其冲激响应来判断。

下图为一系列常用滤波器的冲激响应。

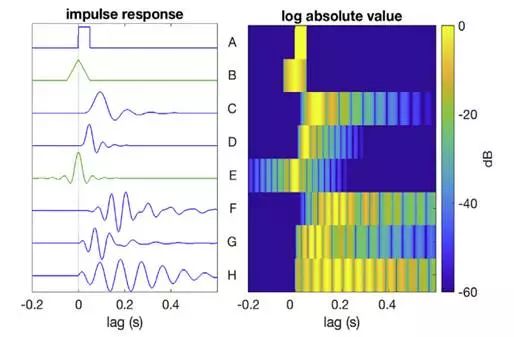
左图为冲激响应的时间序列，横轴为持续时间lag(s)；右图显示了其绝对值的对数(在60 dB处截断)。绿色为非因果滤波器。

可见：高阶滤波器时间跨度更大。带通滤波器具有相对较长的脉冲响应，特别是当带宽较窄时。

但是真实的大脑事件与无限狭窄的单极脉冲不同，因为它们的宽度是有限的，因此对真实大脑事件的反应将与理想的脉冲响应有所不同。在滤波器对大脑事件的响应过程中，宽度大于事件特征宽度的冲激响应是可以被识别的。同时较窄的特征可能出现平滑。

2.阶跃

某些大脑事件可以被建模为阶跃函数。下图说明了滤波可以影响阶跃式大脑事件的各种方式。可以平滑响应（低通滤波器）和延迟响应（因果滤波器）。

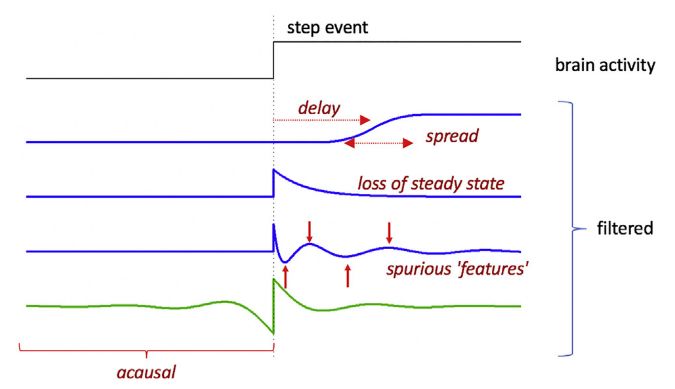
稳态部分可能丢失（高通滤波器），并且可能出现虚假特征，其中一些可能发生在事件之前（非因果滤波器，绿色）。

这些影响的性质还是取决于滤波器。可以从滤波器的阶跃响应(冲激响应随时间的积分)推断出来。

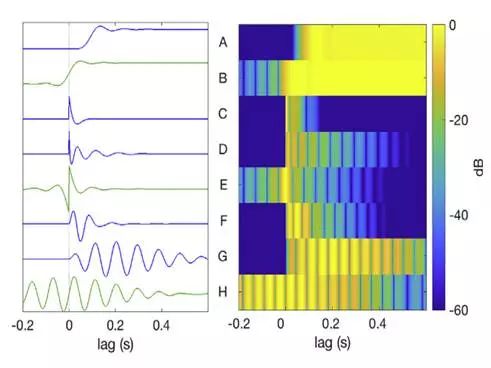
A说明：滤波器为因果会造成事件延迟。

B说明：滤波器为非因果则会提前。

对于高通（C-E）或带通（F-H）滤波器来说，稳态部分会丢失。响应可能包括虚假的偏移，如果滤波器是非因果性的，则其中一些出现在事件之前。(Filtfilt是用于设计非因果滤波器的函数)。

响应还可能是由振铃效应引起的振荡(F-H)。

但是实际的阶跃式大脑活动与理想的阶跃是不同的。在输出中，可以识别出比事件开始时的阶跃响应更宽的阶跃响应，而较窄的会变得平滑。

需要注意的是，稳态部分的偏移会导致相反极性的阶跃响应。

3.振荡活动

大脑中的一些活动是振荡的。这种振荡活动可以被看作是正弦脉冲。

下图为滤波对正弦脉冲的响应：一个脉冲的时间序列受到滤波的影响:它会随着时间的推移而平滑和扩散，如果滤波是因果的，它可能会延迟，如果滤波是非因果的，它可能会比事件开始的更早。

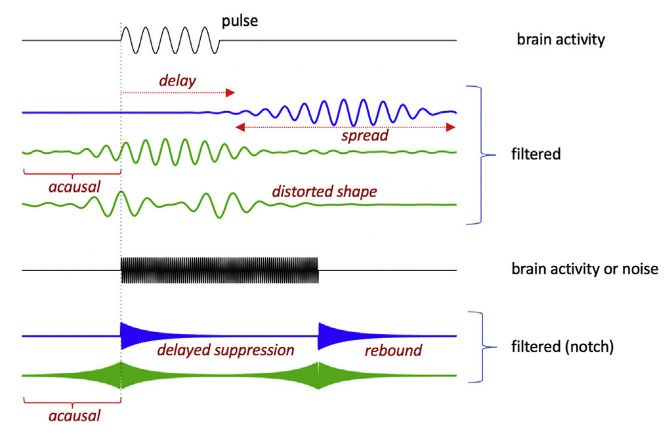
当滤波器的通带较窄时(人们可能想用它来增加这种振荡活动的信噪比)，这种影响就更明显。

对于调到脉冲频率的陷波滤波器，这种抑制可能会延迟，而且在脉冲之后可能会有一个反弹的伪迹(振铃效应)。非因果的话，该伪迹会在事件出现之前或之后出现。

滤波过程中会出现的问题：

1.有用信息的丢失和噪声一起被抑制。

2.目标的时间特征的失真:峰值或过渡带可能被平滑，阶跃可能变成脉冲，并且可能出现伪迹。

3.信号内部特征之间或信号与外部事件(如刺激)之间的时间或因果关系模糊不清。

4.时频（TF）分析

在时频分析中，滤波器涉及的大多是比较底层的数据收集，从而影响最终的时频分析图。

时频分析图就是：在每个时间点，分析产生一个频谱，这些频谱被连接起来形成二维的分析图；或者我们可以将其等价为：在每个频率使用一个滤波器。

下图为：时频分析引起的时间关系模糊

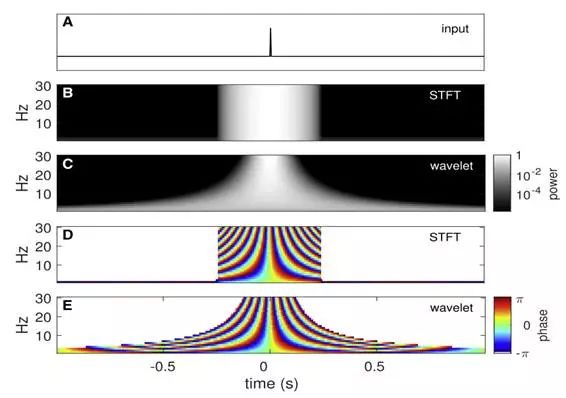
STFT频谱图中，对于所有频率，分析窗口的大小是相同的。相反，在小波频谱图中，这个窗的大小随频率而变化，因为小波变换的每个分析窗口跨越的周期的数量是相同的。

因此，结合前面的内容，TF的结果要么相对于数据中的事件存在延迟(因果分析)，要么在一定程度上反映了未来的事件(非因果分析)。

所以这种模糊的、非因果关系可能会误导最终结论。

①报告完整的滤波器参数

比如说滤波器的类型、阶数、频率参数，以及它是应用于一个方向还是同时应用于两个方向的，还有冲激响应(和/或阶跃响应)的图。

②使用低通时，要确认：是否需要增强图像的清晰度，或者是否要衰减高频功率。

③若仅需要高通滤波器来消除恒定的DC偏移，则考虑采用减去整体均值的方法；如果还有一个缓慢的趋势，请考虑“去趋势”而不是高通滤波。

去趋势引入了一个拟合函数（通过缓慢变化以适应趋势），将该函数拟合到数据然后减去引入的拟合函数。这种合适的拟合函数是一个低阶多项式。

去趋势与滤波一样，去除趋势对类似于毛刺的一类信号很敏感；但是这些可以通过“强有力的去趋势”来解决。

④带通滤波

尽量避免使用带通滤波，因为会带来振铃效应。即使为了提升信噪比而必须使用的话，也要选择具有相对平坦的过渡带和远离目标频段的截止频率的滤波器。

⑤陷波

陷波滤波通常是为了抑制电源噪声。同时作为滤波的替代方案，可以测量一个或多个参考通道上的电源噪声并将其从数据中回归。

如果高频不感兴趣，则可使用1/50 Hz的boxcar平滑内核(一种加矩形窗的函数)。这种简单的低通滤波器在电源工频及其所有谐波处都有零点，从而可以完美消除电源噪声及相关谐波干扰。

⑥时频分析

如果感兴趣的部分可以在时域中解释，那么就可以避免TF分析。如果必须应用TF分析，则考虑使用离散傅里叶变换来进行分析，而不是小波分析。

若要使用小波分析，则应使用相对较短的分析窗口来减少时间偏差，同时仔细考虑因果分析（有相位偏差但没有因果关系问题）和非因果分析（无相位偏差但存在被误认为是因果关系的风险）之间的选择。

要做到以上这些，我们可能需要：

了解我们使用的滤波器；了解存在的噪声；在源头消灭噪声(不太可能)；确保拥有足够的抗混叠；考虑滤波的替代方案；选择正确的滤波器。