基于matlab免疫算法求解生产调度零等待问题

生产调度零等待问题

经典的优化问题，免疫算法（IA）是求解该问题的常用方法之一。其数学原理公式如下：

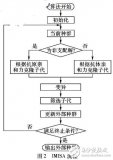
定义问题：生产调度零等待问题可表示为在满足各种制约条件下，找到最小化某个指标（如总加工时间、平均加工时间等）的调度方案。

定义目标函数：目标函数是对待优化的调度方案进行评估的函数，通常为评估调度方案的效果的指标，例如总加工时间、平均加工时间等。

初始化免疫群体：生成一组随机免疫体，作为初始免疫群体。

计算亲和度：对免疫群体中每个免疫体，通过目标函数计算其适应值，得到其在免疫群体中的亲和度。

选择克隆体：根据亲和度，选择一定数量的高亲和度免疫体进行克隆，产生一批克隆体。

变异操作：对克隆体进行变异操作，增加群体的多样性。

竞争操作：将克隆体和原始免疫体进行竞争，筛选出高亲和度的免疫体作为下一代免疫群体。

迭代求解：循环执行步骤4-7，直到达到预先设定的停止条件（如迭代次数或最优适应值达到一定程度）。

输出结果：在最终免疫群体中选择最优免疫体作为最优解输出，得到最优的调度方案。

function [fitness] = fitness_function(chromosome, job_times, machine_num)
    % chromosome 为染色体，表示作业的调度顺序
    num_jobs = length(job_times);
    machine_end_time = zeros(1, machine_num); % 每台机器的结束时间
    job_start_time = zeros(1, num_jobs); % 每个作业的开始时间
    for i = 1 : num_jobs
        job = chromosome(i);
        time = job_times(job);
        [~, machine_id] = min(machine_end_time);
        start_time = max(machine_end_time(machine_id), job_start_time(job));
        end_time = start_time + time;
        machine_end_time(machine_id) = end_time;
        job_start_time(job) = end_time;
    end
    fitness = sum(machine_end_time); % 目标是最小化总加工时间
end


job_times = [2, 9, 4, 7, 5]; % 每个作业的耗时
machine_num = 3; % 机器数量
options = optimoptions('ga', 'MaxGenerations', 100, 'PopulationSize', 50); % 定义GA的参数
[x, fval] = ga(@(x)fitness_function(x, job_times, machine_num), length(job_times), options); % 调用 ga 函数求解


% 输出最优解
disp(x);
disp(fval);

以上代码中，定义了一个适应度函数 fitness_function，该函数根据输入的调度顺序和每个作业的耗时，计算出每台机器的总加工时间，并将其作为函数的返回值。在主程序中，使用 MATLAB 中的 ga 函数进行求解，得到最优的调度顺序和最小的总加工时间。

审核编辑：汤梓红