Poly基本原理及卷积分析示例

**Poly基本原理介绍 **

考虑到许多读者可能对Poly并不了解，而且许多Poly文献读起来也比较抽象，我们先简单介绍一下Poly的工作原理。我们力图用最简单的代数与几何描述来解释Poly的基本原理。这部分内容参考了文献[12]的图片，我们通过解读这些图片来解释其中原理。

首先，我们假设有如图1所示的一段简单的循环嵌套，其中N为常数。循环嵌套内语句通过对A[i-1][j]和A[i][j-1]存储数据的引用来更新A[i][j]位置上的数据。如果我们把语句在循环内的每一次迭代实例抽象成空间上的一个点，那么我们可以构造一个以(i,j)为基的二维空间，如图2所示。图中每个黑色的点表示写入A[i][j]的一次语句的迭代实例，从而我们可以构造出一个所有黑色的点构成的一个矩形，这个矩形就可以看作是二维空间上的一个Polyhedron（多面体），这个空间称为该计算的迭代空间。

图1 一段简单的代码示例

图2 图1示例代码的迭代空间

我们可以用代数中的集合来对这个二维空间上的Polyhedron进行表示，即{[i, j] : 1 <= i <= N - 1 and 1 <= j <= N – 1}，其中[i, j]是一个二元组，“:”后面的不等式表示这个集合的区间。我们可以给这个二元组做一个命名，叫做S，表示一个语句，那么这个语句的Polyhedron就可以表示成{S[i, j] : 1 <= i <= N - 1 and 1 <= j <= N – 1}。

由于语句S是先迭代i循环再迭代j循环，因此我们可以给语句S定义一个调度（顺序），这个调度用映射表示，即{ S[i, j] -> [i, j] }，表示语句S[i, j] 先按i的顺序迭代再按照j的顺序迭代。

接下来，我们来分析语句和它访存的数组之间的关系，在代数中我们用映射来表示关系。图1中语句S对数组A进行读和写，那么我们可以用Poly来计算出S和A之间的读访存关系，可以表示成{ S[i, j] -> A[i - 1, j] : 1 <= i <= N -1 and 1 <= j <= N- 1; S[i, j] -> A[i, j - 1] : 1 <= i <= N - 1 and 1 <= j <= N -1 } 。同样地，写访存关系可以表示成{ S[i, j] -> A[i, j] : 1 <= i <= N - 1 and 1 <= j <= N -1 }。

基于这个读写访存关系，Poly就可以计算出这个循环嵌套内的依赖关系，这个依赖关系可以表示成另外一种映射关系，即{ S[i, j] -> S[i, 1 + j] : 1 <= i <= N - 1 and 1 <= j <=N - 2; S[i, j] -> S[i + 1, j] : 1 <= i <= N - 2 and 1 <= j <= N- 1 }。

可以注意到，Poly对程序的表示都是用集合和映射来完成的。当我们把语句实例之间的依赖关系用蓝色箭头表示在迭代空间内时，就可以得到如图3所示的形式。根据依赖的基本定理[13]，没有依赖关系的语句实例之间是可以并行执行的，而图中绿色带内（对角线上）的所有点之间没有依赖关系，所以这些点之间可以并行执行。但是我们发现这个二维空间的基是(i, j)，即对应i和j两层循环，无法标记可以并行的循环，因为这个绿色带与任何一根轴都不平行。所以Poly利用仿射变换把基(i, j)进行变换，使绿色带能与空间基的某根轴能够平行，这样轴对应的循环就能并行，所以我们可以将图3所示的空间转化成如图4所示的形式。

此时，语句S的调度就可以表示成{ S[i, j] -> [i + j, j]}的形式。所以Poly的变换过程也称为调度变换过程，而调度变换的过程就是变基过程、实现循环变换的过程。

图3 带依赖关系的迭代空间

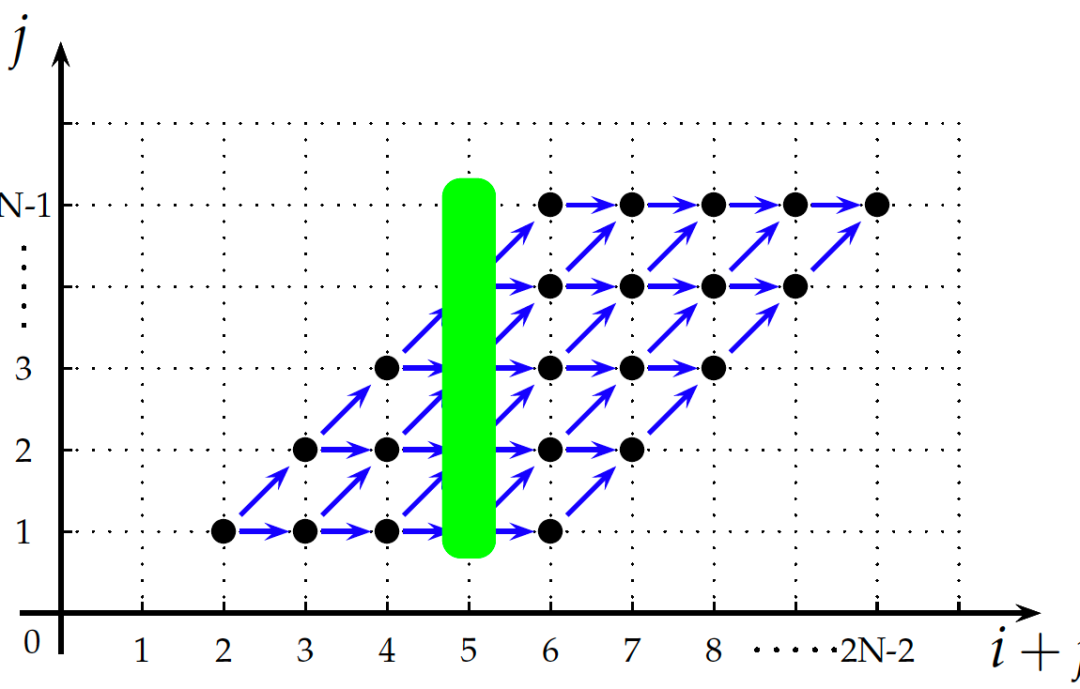
图4 变基之后的迭代空间

图4中绿色带和j轴平行，这样在代码中表示起来就方便了。我们说Poly做循环变换的过程就是将基(i, j)变成(i + j, j)的一个过程，也就是说，Poly的底层原理就是求解一个系数矩阵，这个系数矩阵能够将向量(i, j)转换成向量(i + j, j)。

根据这样的调度，Poly就可以利用它的代码生成器，生成如图5所示的代码。此时，内层循环就可以并行了。（注：这里示意的是“源到源”翻译的Poly编译器，也就是Poly生成的代码还需要交给基础编译器如GCC、ICC、LLVM等编译成机器码才能运行。也有内嵌在基础编译中的Poly工具。）

图5 Poly变换后生成的代码

当然，我们这里举的例子是一个很简单的例子，在实际应用中还有很多复杂的情况要考虑。Poly几乎考虑了所有的循环变换，包括Interchange（交换）、Skewing/Shifting（倾斜/偏移）、Reversal（反转）、Tiling/Blocking（分块）、Stripe-mining、Fusion（合并）、Fission/Distribution（分布）、Peeling（剥离）、Unrolling（展开）、Unswitching、Index-set splitting、Coalescing/Linearization等，图6～8[14]中给出了几种Poly中实现的循环变换示意图，右上角的代码表示原输入循环嵌套，右下角的代码表示经过Poly变换后生成的代码。图中左边的集合和映射关系的含义分别为：J代表原程序语句的迭代空间，S表示输入程序时的调度，T表示目标调度，ST就是Poly要计算的调度变换。

图6 Poly中skewing变换示意图

图7 Poly中Fusion变换示意图

图8 Poly中Tiling变换示意图

深度学习应用的Poly优化

让我们以图9中所示的二维卷积运算（矩阵乘法）为例来简单介绍Poly是如何优化深度学习应用的。

图9 一个2D卷积示例

Poly会将循环嵌套内的计算抽象成一个语句。例如图9中S1语句表示卷积初始化，S2代表卷积归约；而S0和S3则分别可以看作卷积操作前后的一些操作，比如S0可以想象成是量化语句，而S3可以看作是卷积后的relu操作等。

为了便于理解，我们以CPU上的OpenMP程序为目标对图9中的示例进行变换。Poly在对这样的二维卷积运算进行变换的时候，会充分考虑程序的并行性和局部性。如果我们对变换后的程序并行性的要求大于局部性的要求，那么Poly会自动生成如图10所示的OpenMP代码；如果我们对局部性的要求高于并行性，那么Poly会自动生成如图11所示的OpenMP代码。（注：不同的Poly编译器生成的代码可能会因采用的调度算法、编译选项、代码生成方式等因素而不同。）

图10 Poly生成的OpenMP代码——并行性大于局部性

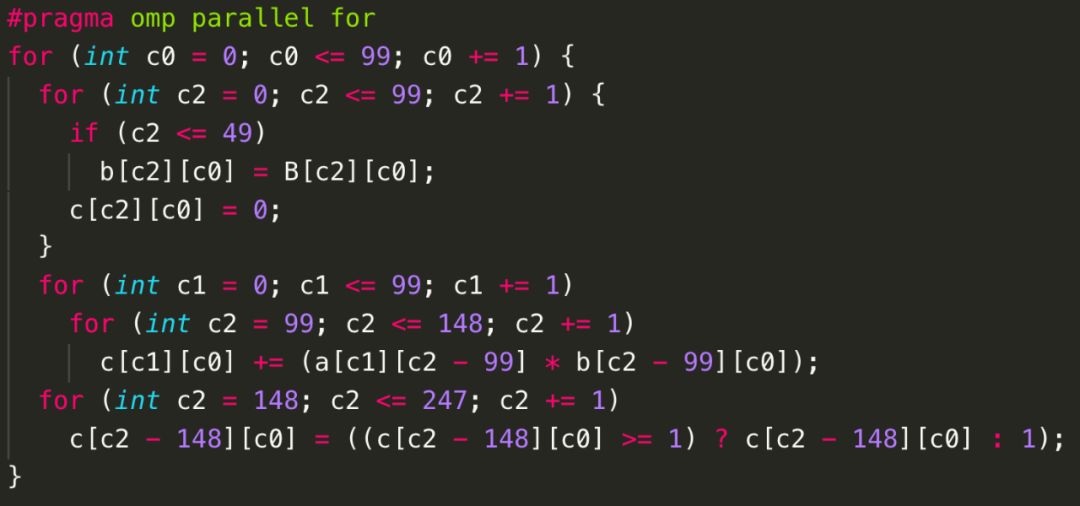
图11 Poly生成的OpenMP代码——局部性大于并行性

通过对比图10和图11，两种生成的代码采用的循环fusion（合并）策略不同：图10中所示的代码采用了({S0}, {S1, S2, S3})的合并策略，图11中生成的代码则使用了({S0,S1, S2, S3})的合并策略，但是必须通过对S2向右偏移99次、S3向右偏移148次，以及循环层次的interchange（交换）来实现这样的合并。显然，图11所示的代码局部性更好。而并行性上，仔细研究后不难发现，图11生成的代码中，只有最外层c0循环是可以并行的，而图10代码中，S0语句的c0、c1循环都可以并行，并且包含S1、S2、 S3三条语句的循环嵌套的c0、c1循环也都可以并行，相对于图11代码，图10生成的代码可并行循环的维度更多。

当然，在面向CPU生成OpenMP代码时，多维并行的优势没有那么明显，但是当目标架构包含多层并行硬件抽象时，图9中的代码能够更好地利用底层加速芯片。例如，当面向GPU生成CUDA代码时，而图10对应的CUDA代码（如图12所示）由于合并成了两个部分，会生成2个kernel，但是每个kernel内c0维度的循环被映射到GPU的线程块上，而c1维度的循环被映射到GPU的线程上；图11对应的CUDA代码（如图13所示）只有1个kernel，但是只有c0维度的循环被映射到GPU的线程块和线程两级并行抽象上。为了便于阅读，我们并未开启GPU上shared memory和private memory自动生成功能。从图中也不难发现，Poly也可以自动生成线程之间的同步语句。（注：图中循环分块大小为32，图12中线程块上线程布局为3216，图13中为324*4。）

图12 Poly生成的CUDA代码——并行性大于局部性

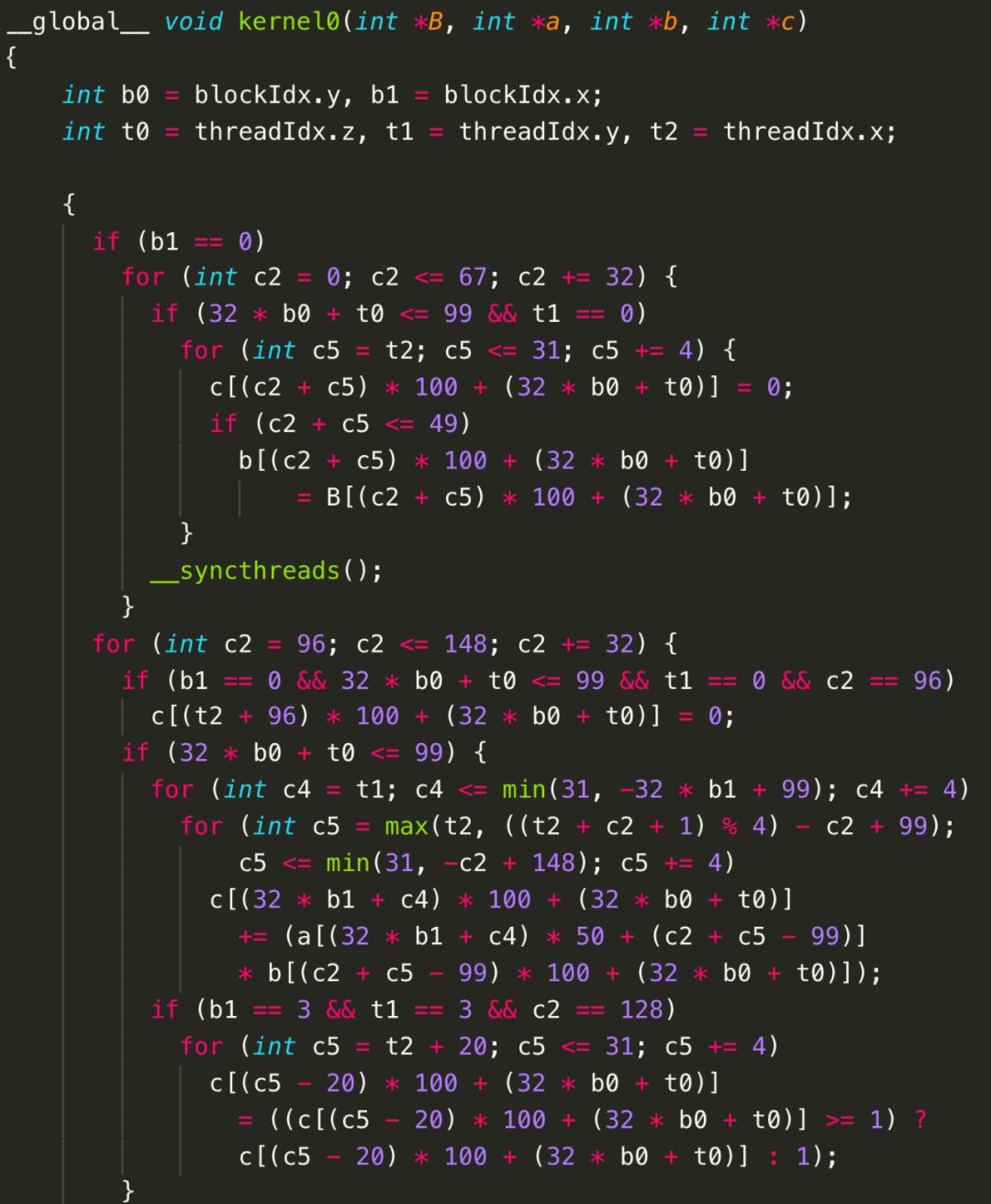
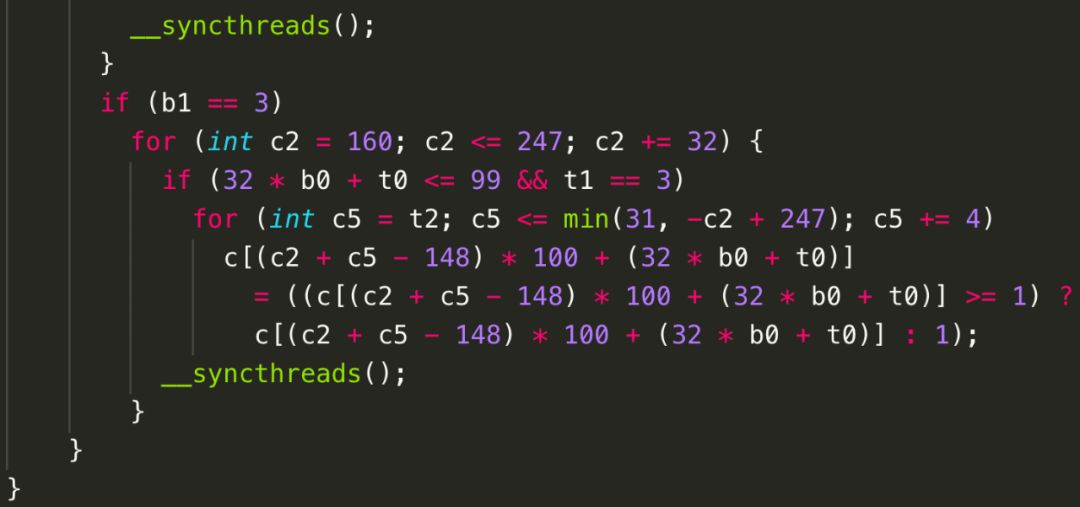
图13 Poly生成的CUDA代码——局部性大于并行性

值得注意的是，为了充分挖掘程序的并行性和局部性，Poly会自动计算出一些循环变换来实现有利于并行性和局部性的变换。例如，为了能够达到图11和图13中所有语句的合并，Poly会自动对S2和S3进行shifting（偏移）和interchange（交换）。