简介
本文主要给定一小段音频,通过短时傅里叶变换和小波变换制作时频图。音频的采样率为44100,
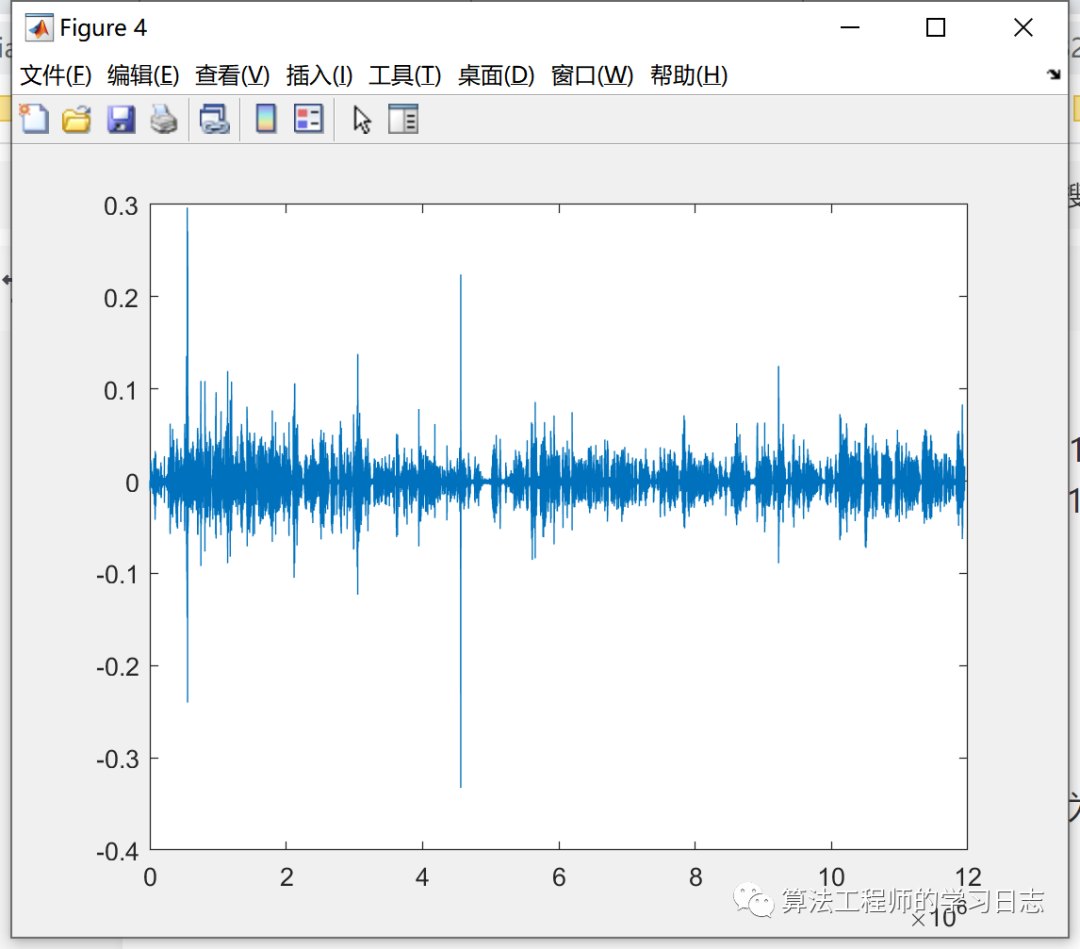
短时傅里叶变换
在matlab中,短时傅里叶变换的分析函数为spectrogram,其使用情况如下:
功能 :使用短时傅里叶变换得到信号的频谱图。
语法 :
[S,F,T,P]=spectrogram(x,window,noverlap,nfft,fs)
[S,F,T,P]=spectrogram(x,window,noverlap,F,fs)
说明:当使用时无输出参数,会自动绘制频谱图;有输出参数,则会返回输入信号的短时傅里叶变换。当然也可以从函数的返回值S,F,T,P绘制频谱图,具体参见例子。
参数 :
x---输入信号的向量。默认情况下,即没有后续输入参数,x将被分成8段分别做变换处理,如果x不能被平分成8段,则会做截断处理。默认情况下,其他参数的默认值为:window---窗函数,默认为nfft长度的海明窗Hamming;noverlap---每一段的重叠样本数,默认值是在各段之间产生50%的重叠;nfft---做FFT变换的长度,默认为256和大于每段长度的最小2次幂之间的最大值。另外,此参数除了使用一个常量外,还可以指定一个频率向量F;fs---采样频率,默认值归一化频率。
Window---窗函数,如果window为一个整数,x将被分成window段,每段使用Hamming窗函数加窗。如果window是一个向量,x将被分成length(window)段,每一段使用window向量指定的窗函数加窗。所以如果想获取specgram函数的功能,只需指定一个256长度的Hann窗。
Noverlap---各段之间重叠的采样点数。它必须为一个小于window或length(window)的整数。其意思为两个相邻窗不是尾接着头的,而是两个窗有交集,有重叠的部分。
Nfft---计算离散傅里叶变换的点数。它需要为标量。
Fs---采样频率Hz,如果指定为[],默认为1Hz。
S---输入信号x的短时傅里叶变换。它的每一列包含一个短期局部时间的频率成分估计,时间沿列增加,频率沿行增加。如果x是长度为Nx的复信号,则S为nfft行k列的复矩阵,其中k取决于window,如果window为一个标量,则k = fix((Nx-noverlap)/(window-noverlap));如果window为向量,则k = fix((Nx-noverlap)/(length(window)-noverlap))。对于实信号x,如果nfft为偶数,则S的行数为(nfft/2+1),如果nfft为奇数,则行数为(nfft+1)/2,列数同上。
F---在输入变量中使用F频率向量,函数会使用Goertzel方法计算在F指定的频率处计算频谱图。指定的频率被四舍五入到与信号分辨率相关的最近的DFT容器(bin)中。而在其他的使用nfft语法中,短时傅里叶变换方法将被使用。对于返回值中的F向量,为四舍五入的频率,其长度等于S的行数。
T---频谱图计算的时刻点,其长度等于上面定义的k,值为所分各段的中点。
P---能量谱密度PSD(Power Spectral Density),对于实信号,P是各段PSD的单边周期估计;对于复信号,当指定F频率向量时,P为双边PSD。P矩阵的元素计算公式如下P(I,j)=k|S(I,j)|2,其中的的k是实值标量,定义如下对于单边PSD,计算公式如下,其中w(n)表示窗函数,Fs为采样频率,在0频率和奈奎斯特频率处,分子上的因子2改为1;
MATLAB程序:
[Au, Fs]=audioread('audio.mp3'); % Fs 采样率 44100
[B, F, T, P] = spectrogram(Au(:,1),1024,512,1024,Fs); % B是F大小行T大小列的频率峰值,P是对应的能量谱密度
figure
imagesc(T,F,10*log10(abs(P)));
set(gca,'YDir','normal')
colorbar;
xlabel('时间 t/s');
ylabel('频率 f/Hz');
title('短时傅里叶时频图');
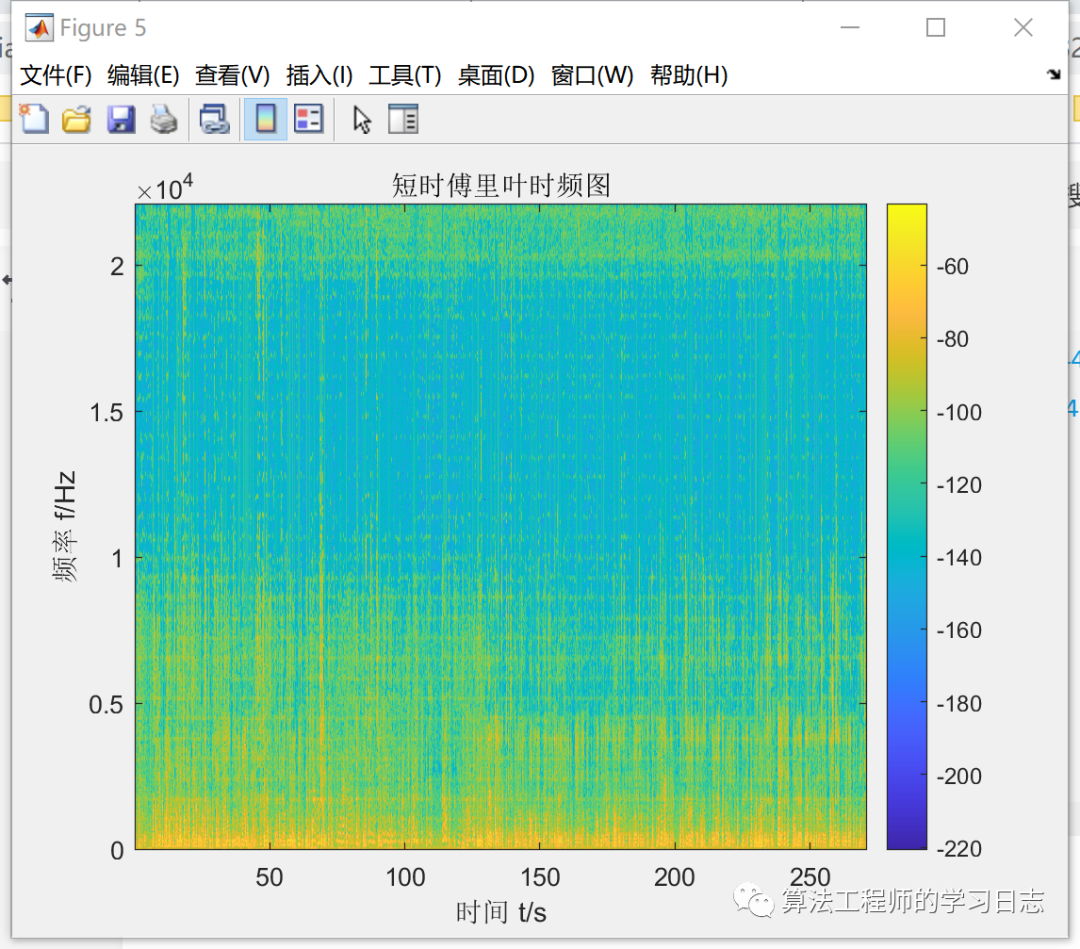
注意:
- nfft越大,频域的分辨率就越高(分辨率=fs/nfft),但离瞬时频率就越远;
- noverlap影响时间轴的分辨率,越接近nfft,分辨率越高,相应的冗余就越多,计算量越大,但计算机只要能承受,问题不大。
小波变换
首先,在matlab中,小波变换的分析函数为cwt,其使用情况如下:
功能 :实现一维连续小波变换的函数。
语法 :
COEFS=cwt(S, SCALES, 'wname')
COEFS=cwt(S, SCALES, 'wname', 'plot')
COEFS=cwt(S, SCALES, 'wname', 'PLOTMODE')
COEFS=cwt(S, SCALES, 'wname', 'PLOTMODE', XLIM)
参数 :
COEFS=cwt(S, SCALES, 'wname') 采用'wname'小波,在正、实尺度SCALES下计算向量一维小波系数。
COEFS=cwt(S, SCALES, 'wname', 'plot') 除了计算小波系数外,还加以图形显示。
COEFS=cwt(S, SCALES, 'wname', 'PLOTMODE') 计算并画出连续小波变换的系数,并使用PLOTMODE对图形着色。
COEFS=cwt(S, SCALES, 'wname', 'plot') 相当于 格式 COEFS=cwt(S, SCALES, 'wname', 'PLOTMODE') 中的语法 COEFS=cwt(S, SCALES, 'wname', 'absglb')
COEFS=cwt(S, SCALES, 'wname', 'PLOTMODE', XLIM) 能够计算并画出连续小波变换的系数。系数使用PLOTMODE和XLIM进行着色。其中:XLIM=[x1,x2],并且有如下关系:1<=x1<=x2<=length(S)。
MODE值含义:
'lvl' scale-by-scale着色模式
'glb' 考虑所有尺度的着色模式
'abslvl'或'lvlabs' 使用系数绝对值的scale-by-scale着色模式
'absglb'或'glbabs' 使用系数绝对值并考虑所有尺度的着色模式
COEFS行的大小等于SCALES尺度的长度,COEFS列的大小等于信号S的长度。
MATLAB程序:
totalscal=1024*16;
wavename='cmor3-3';
Fc=centfrq(wavename); % 小波的中心频率
c=2*Fc*totalscal;
scals=c./(1:totalscal);
f=scal2frq(scals,wavename,1/Fs); % 将尺度转换为频率 频率在0-500Hz取1024
coefs = cwt(Au(totalscal,1),scals,wavename); % 求连续小波系数
t=0:1/Fs:(totalscal-1)/Fs;
figure
imagesc(t,f,abs(coefs));
set(gca,'YDir','normal')
colorbar;
xlabel('时间 t/s');
ylabel('频率 f/Hz');
title('小波时频图');
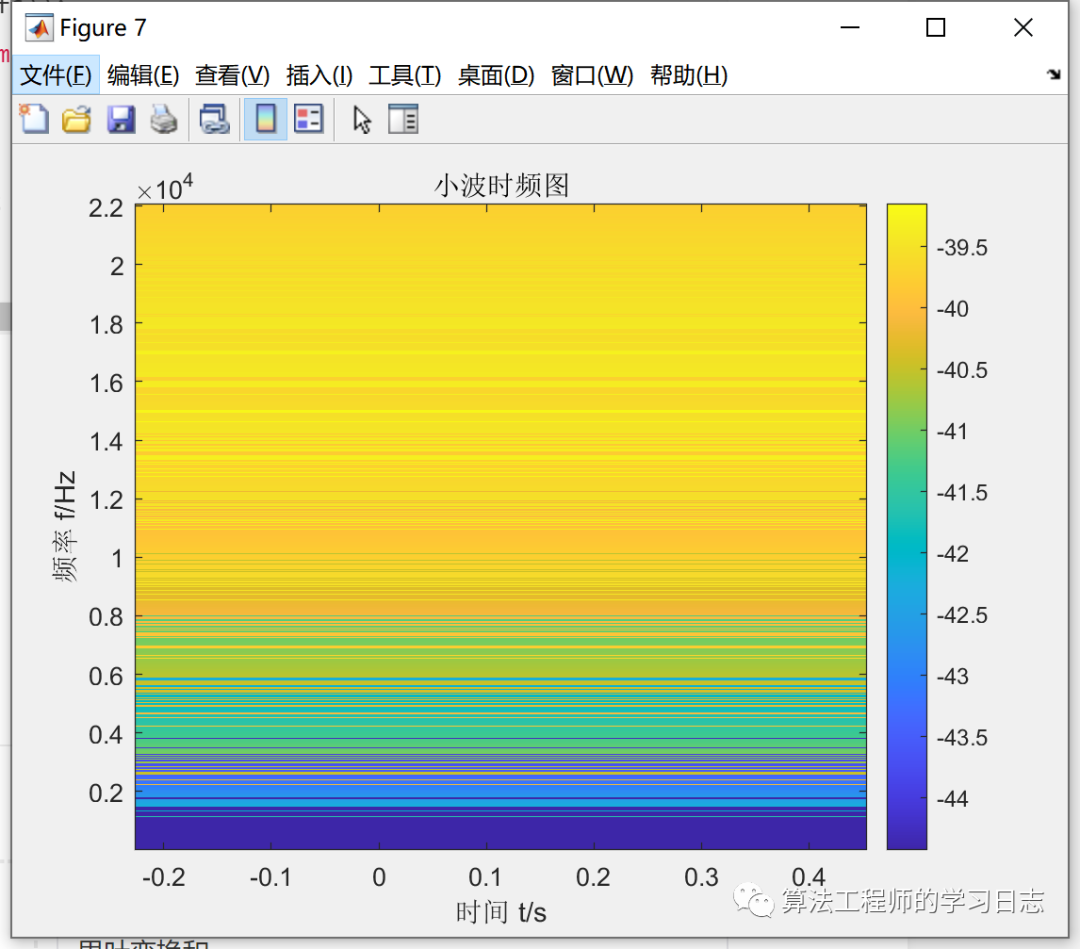
-
小波变换
+关注
关注
2文章
183浏览量
29719 -
PSD
+关注
关注
0文章
35浏览量
45384 -
MATLAB仿真
+关注
关注
4文章
176浏览量
19908 -
频谱仪
+关注
关注
7文章
339浏览量
36003 -
傅里叶变换
+关注
关注
6文章
438浏览量
42573
发布评论请先 登录
相关推荐
DSP变换运算-傅里叶变换
基于短时傅里叶变换的OFDM时间同步方法

傅里叶变换的介绍傅里叶变换有什么意义和应用





 谈谈Matlab短时傅里叶变换和小波变换的时频
谈谈Matlab短时傅里叶变换和小波变换的时频












评论