matlab-粒子群算法优化simulink中的pid参数详解

PSO（粒子群算法）在处理连续问题上有着较强的能力，因此很适合用来做参数优化，而PID控制器由三个参数组成，它们分别是：Kp 、Ki 、Kd 。

我们可以把PID控制器当做一个“黑箱”，输入为这三个参数，输出为响应曲线，我们要做的就是优化这个响应曲线。而一个控制效果好的PID控制器应针对不同类型输入都有较快的响应速度，较小的超调以及稳态误差。在本次分享中，选择输入信号为阶跃输入用来衡量PID控制效果。

PSO的适应函数选用综合指标来衡量设计效果，由于是数字控制器，我们选用求和而不是积分的方式：

在特定的问题中，这个适应函数也可以按照实际需求修改，比如分析超调量、稳定时间等，具体问题具体分析

PSO的主函数和之前的案例类似

参数设置

wmax = 1;     % 最大惯性因子 
wmin = 0.6;   % 最小惯性因子 


% w = 0.6;      % 惯性因子 
c1 = 2;       % 加速常数
c2 = 2;       % 加速常数


Dim = 3;            % 维数
SwarmSize = 30;    % 粒子群规模
ObjFun = @PSO_PID;  % 待优化函数句柄


MaxIter = 10;      % 最大迭代次数  
MinFit = 0.1;       % 最小适应值 


Vmax = 1;
Vmin = -1;
Ub = [300 300 300];
Lb = [0 0 0];

其中的Ub和Lb分别是kp ki kd的上下限，开始优化的时候可以设置大一点，如果大概知道范围，也可以缩小范围，减少迭代次数

粒子群初始化

Range = ones(SwarmSize,1)*(Ub-Lb);
Swarm = rand(SwarmSize,Dim).*Range + ones(SwarmSize,1)*Lb;      % 初始化粒子群
VStep = rand(SwarmSize,Dim)*(Vmax-Vmin) + Vmin;                 % 初始化速度
fSwarm = zeros(SwarmSize,1);
for i=1:SwarmSize
    fSwarm(i,:) = PSO_PID(Swarm(i,:));                         % 粒子群的适应值
end


%% 个体极值和群体极值
[bestf,bestindex]=min(fSwarm);
zbest=Swarm(bestindex,:);   % 全局最佳
gbest=Swarm;                % 个体最佳
fgbest=fSwarm;              % 个体最佳适应值
fzbest=bestf;               % 全局最佳适应值

迭代寻优

iter = 0;
y_fitness = zeros(1,MaxIter);   % 预先产生4个空矩阵
K_p = zeros(1,MaxIter);         
K_i = zeros(1,MaxIter);
K_d = zeros(1,MaxIter);
while( (iter < MaxIter) && (fzbest > MinFit) )
    w = wmax-(wmax-wmin)/MaxIter*iter;  %% 惯性权重因子调整
    for j=1:SwarmSize
        % 速度更新
        VStep(j,:) = w*VStep(j,:) + c1*rand*(gbest(j,:) - Swarm(j,:)) + c2*rand*(zbest - Swarm(j,:));
        if VStep(j,:) >Vmax, VStep(j,:)=Vmax; end
        if VStep(j,:)< Vmin, VStep(j,:)=Vmin; end
        % 位置更新
        Swarm(j,:)=Swarm(j,:)+VStep(j,:);
        for k=1:Dim
            if Swarm(j,k) >Ub(k), Swarm(j,k)=Ub(k); end
            if Swarm(j,k)< Lb(k), Swarm(j,k)=Lb(k); end
        end
        % 适应值
        fSwarm(j,:) = PSO_PID(Swarm(i,:));
        % 个体最优更新     
        if fSwarm(j) < fgbest(j)
            gbest(j,:) = Swarm(j,:);
            fgbest(j) = fSwarm(j);
        end
        % 群体最优更新
        if fSwarm(j) < fzbest
            zbest = Swarm(j,:);
            fzbest = fSwarm(j);
        end
    end 
    iter = iter+1;                      % 迭代次数更新
    y_fitness(1,iter) = fzbest;         % 为绘图做准备
    K_p(1,iter) = zbest(1);
    K_i(1,iter) = zbest(2);
    K_d(1,iter) = zbest(3);
end

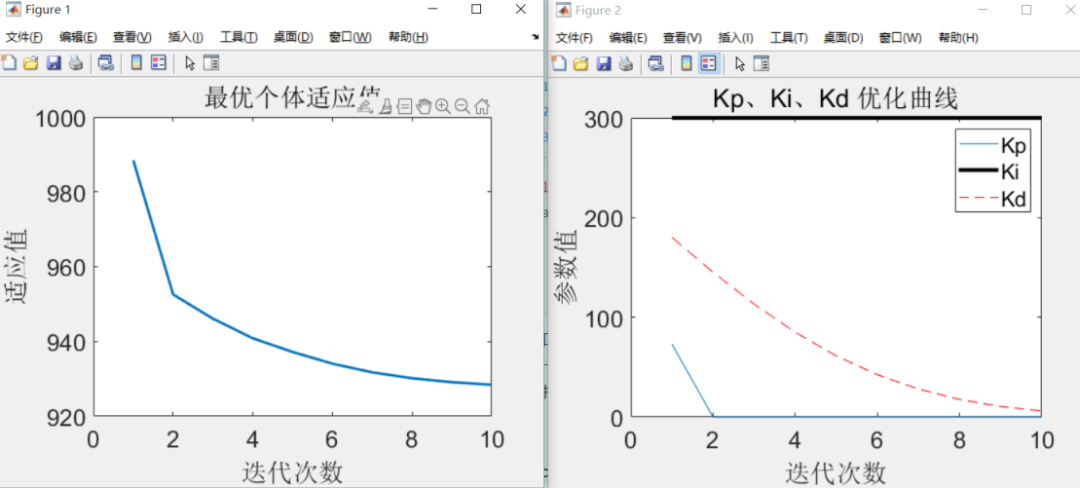
绘图输出

figure     % 绘制性能指标ITAE的变化曲线
plot(y_fitness,'LineWidth',2)
title('最优个体适应值','fontsize',18);
xlabel('迭代次数','fontsize',18);ylabel('适应值','fontsize',18);
set(gca,'Fontsize',18);


figure      % 绘制PID控制器参数变化曲线
plot(K_p)
hold on
plot(K_i,'k','LineWidth',3)
plot(K_d,'--r')
title('Kp、Ki、Kd 优化曲线','fontsize',18);
xlabel('迭代次数','fontsize',18);ylabel('参数值','fontsize',18);
set(gca,'Fontsize',18);
legend('Kp','Ki','Kd');

目标函数设计

function z=PSO_PID(x)
assignin('base','Kp',x(1));    %粒子依次赋值给Kp
assignin('base','Ki',x(2));    %粒子依次赋值给Ki
assignin('base','Kd',x(3));    %粒子依次赋值给Kd
try  %% simulink仿真异常，返回一个极大值
    y_out=sim('PID_Model',[0,20]);    %使用命令行运行控制系统模型
    z = y_out.yout{1}.Values.Data(end);
catch
    z=1e6;
end

代码中assignin实现了m文件和simulink传递参数，其中y_out是simulink输出的目标变量，为啥这儿需要一个try呢，因为这个优化的过程中，可能参数设置不合理，会抛出simulink报错，故增加一个try避免代码异常出错提前结束优化过程

simulink模型用一个简单的pid控制带时延的传递函数

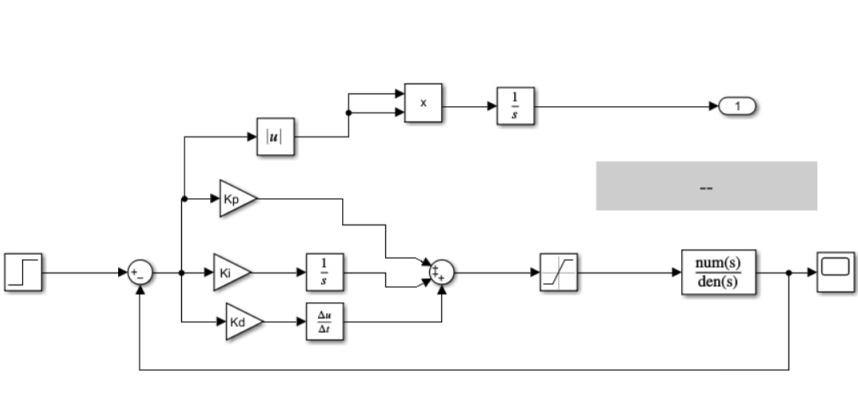
仿真结果类似这样，因为迭代次数很少，设计中可以加大，得到更优的结果