两种含义
学习信号处理经常会被各种变换搞得晕头转向,这也是很正常的事,大可不必惊慌。晕的原因有两个,一是各种变换公式看上去差不多,中间有或多或少的联系,但又很不一样,可能适用于不同的情况,有不同的限制等;二是这门学科确实起名太混淆了点,比如DTFT(Discrete Time Fourier Transform,离散时间傅里叶变换),DFT(Discrete Fourier Transform,离散傅里叶变换),DFS(Discrete Fourier Series,离散傅里叶级数),FFT(Fast Fourier Transform,快速傅里叶变换)。这些变换名字差不多,公式也差不多,不太容易搞清楚各自确切的含义和互相的联系。
本文不去很深入的研究每一个变换,只关注工程实践中最常用的FFT,来简单剖析一下它的含义,性质和一些用法。
FFT的含义可以从两个角度去理解,首先是DFS角度,其次是DTFT角度。
从DFS角度来说:FFT本质上就DFT,而DFT和DFS没有什么不同。
第一句很好理解,因为FFT就是DFT的快速算法。
快了多少呢?DFT的时间复杂度是N^2,FFT的时间复杂度是NlogN。所以,假设N=1024,那就快了N/logN=102.4倍,可以说天壤之别。
现在看DFS:
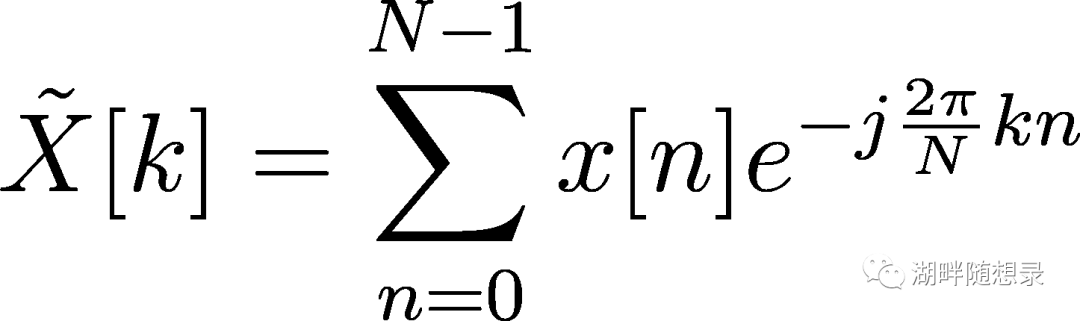
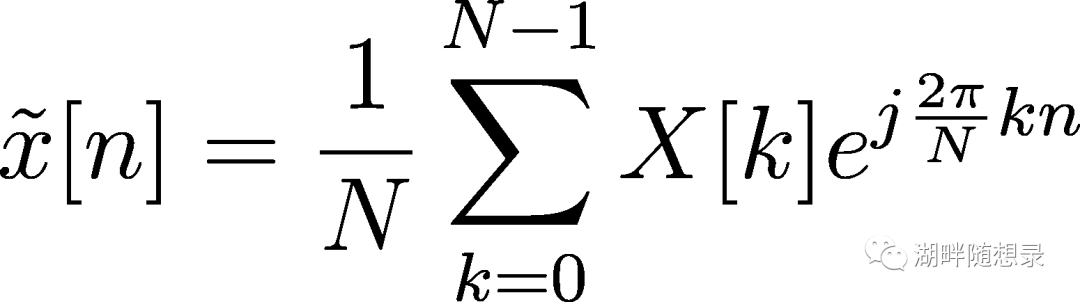
DFS是离散周期序列x[n]到离散周期序列X[k]的变换,x[n]和X[k]周期相同均为N。因为非周期信号工程中更常见,科学家们就截取了DFS对的各自一个周期,定义为DFT变换。这样DFT本质上就是DFS,只是隐含了周期性的假设。
所以,对一个非周期信号x[n]进行长度为N的DFT变换,首先是对x[n]进行周期为N的周期延拓,再求这个周期信号的DFS变换X(k),最后截取X(k)一个周期,就得到x[n]的DFT。
因为离散序列通过DFT(或DFS)变换后还是离散序列,这意味着变换前后都很方便用计算机处理,所以DFT在实践中非常重要。
另外还可以从DTFT的角度来理解FFT。
先看DTFT的公式:
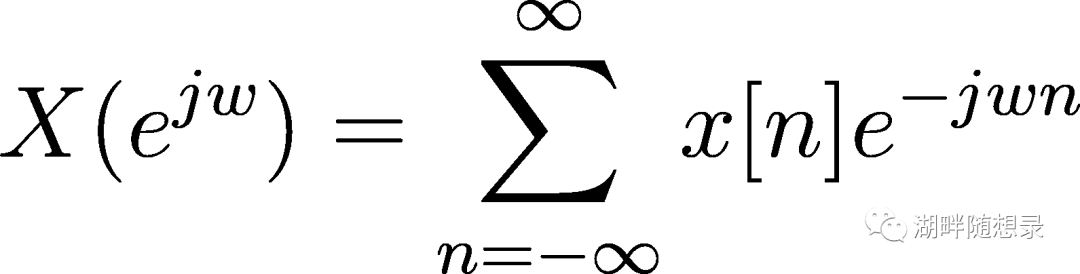
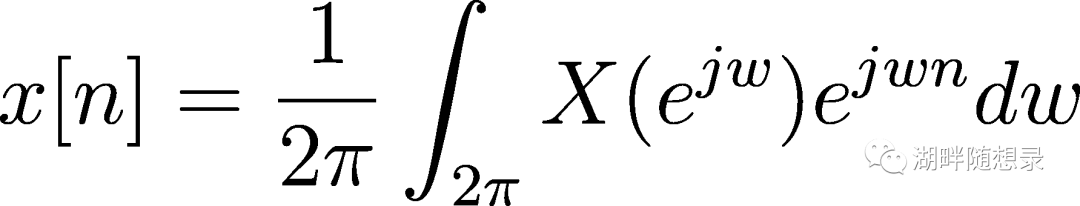
DTFT是离散非周期信号到连续周期信号的变换,频域是周期连续信号,显然是以2Pi为周期(所有频率都是以2Pi为周期)。DFS是对这个非周期信号进行周期延拓,在频域就是对DTFT进行采样。我们可以认为DFS设定的信号的周期延拓的周期N(也就是FFT的长度N)为DTFT一个周期内的采样个数,N设定的越长,采样越频繁。
比如下图:
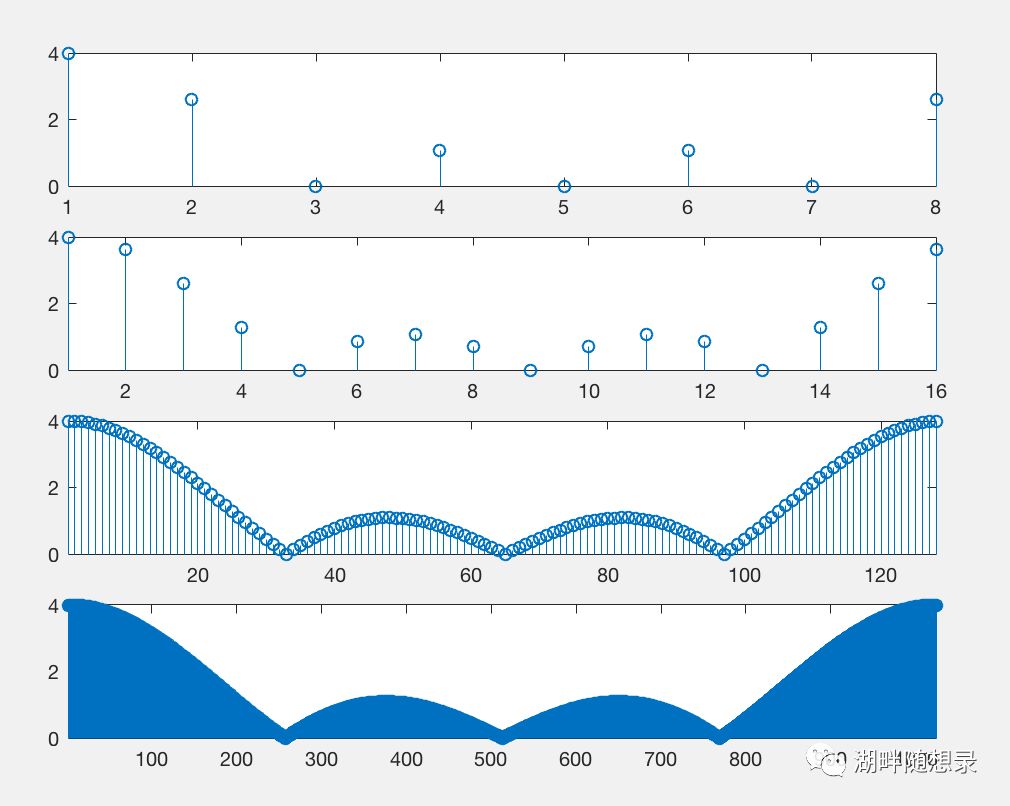
图1 一个 [1 1 1 1] 的有限长序列分别进行长度为8,16,128,1024的FFT
可见DFS选择不同的周期N延拓非周期信号的时候,相当于对DTFT的每个周期进行采样点为N的采样。因为DTFT以[0, 2Pi)为周期,则DFS中0对应频率0,N对应频率2Pi。
注意上面都是说的DFS,而FFT本质上就是DFS。
N的选择
计算FFT的时候,最好选择长度N为2的n次幂,即N=2^n。因为FFT是采用“分治”(divide-and-conquer)思想实现的算法,层层二分显然是最好的分治,这样长度就需要是2的N次幂。现代的FFT算法也支持长度N为任意值,都可以得到正确的结果,只是速度上的快慢差别而已。最慢的情况是N是一个质数,这样算法无法进行任何的分解,好一点的情况是N是一个非质数,最好的情况是N是2的n次幂。比如我们用 Matlab(R2016a)做一个实验:
代码:
A=[1,2,3];
tic
fft(A, 121000);
toc;
tic
fft(A, 121001);
toc;
tic
fft(A, 131072);
toc;
结果:
Elapsed time is 0.006575 seconds.
Elapsed time is 0.039950 seconds.
Elapsed time is 0.004747 seconds.
当N等于质数121001时,FFT的运行时间大概是121000时的6倍,而N取值131072(2^17)时算得最快。
一些性质
共轭对称
从FFT的公式可轻松推出,FFT变换后,第k个频点和第N-k个频点是共轭关系。这样,第k个频点的信息量完全等于第N-k个频点的信息量,因此在频域我们可以只处理差不多一半的频点,处理完毕后再利用共轭的性质把另一半恢复出来,减少了一半的计算量。但这个“差不多一半”不是精确的“N/2”,而是N/2+1。因为频点的取值范围是[0, N-1],0频点没有频点和它共轭,但必须把它算在信息里面。
相位信息
信号的相位信息,在经过FFT之后,通过 arctan(X) 反映出来,比如求这个信号的相位信息:
smallvalue = 1e-10;
fs = 1000;
N = 1000;
t = (0:N-1)/fs;
f=linspace(0,fs,N+1);
f1= 50;
y = cos(2*pi*f1*t+pi/4);
Y = fft(y);
Y(intersect(find(real(Y)< smallvalue), find(imag(Y)< smallvalue)))=0;
plot(f(1:N),angle(Y));
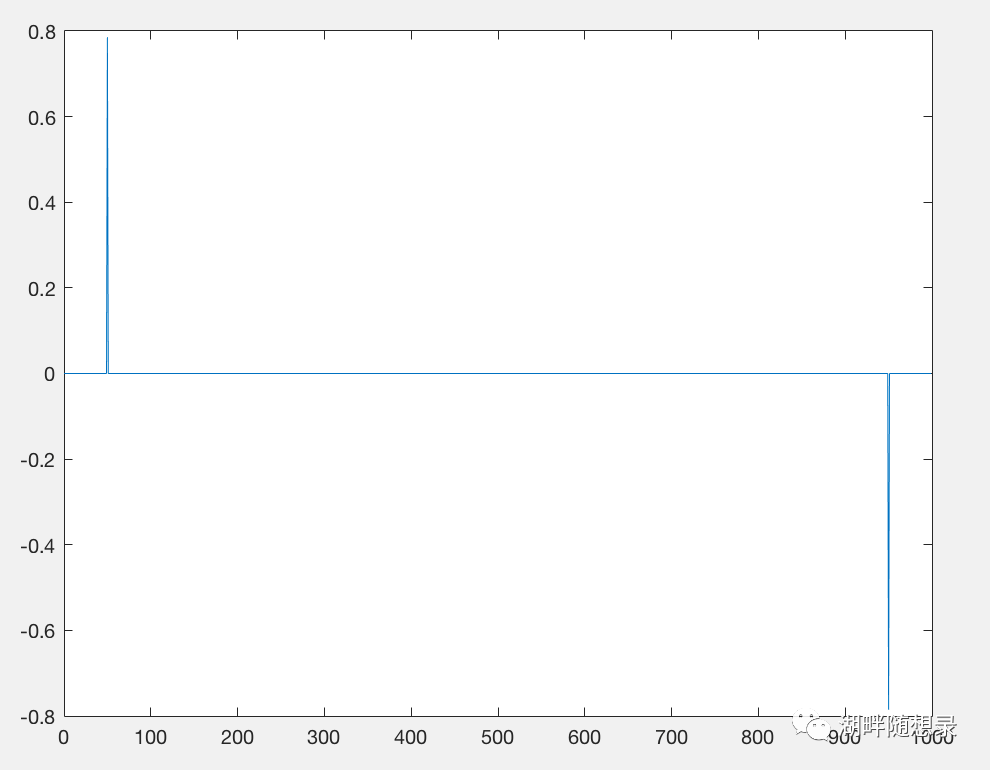
图二 信号的相位信息
注意,如果FFT计算出的复数等于0的话,因为 Matlab 的计算精度问题,其实都是一些很小的值,比如实部 re = 1.05e-12,虚部 im = 3e-12。这些值对功率谱没什么影响,但取 arctan(im/re) 时却是一些很大的值,范围在[-Pi, Pi],这显然是不合理的。
所以我手动去掉了某些极小值。
Y(intersect(find(real(Y)
加窗
在实际应用中,对一段信号做FFT通常要先加窗,根本原因也是FFT隐藏的周期性。
比如分别对下图第一列中的两个信号求FFT,首先是做周期延拓,再求DFS。第一行的信号,周期延拓后正好是一个完美的连续函数,DFT完全不受影响,仍然只有原始信号的频率,其实就是一个单一频率。而第二行的信号,周期延拓后变成了一个不连续的函数,简单的说,也就是引入了其他频率分量,因此DFT后产生了原始信号没有的频率,这就叫频谱泄漏。
而加窗使得信号周期延拓后变得连续,减少了频谱泄漏。
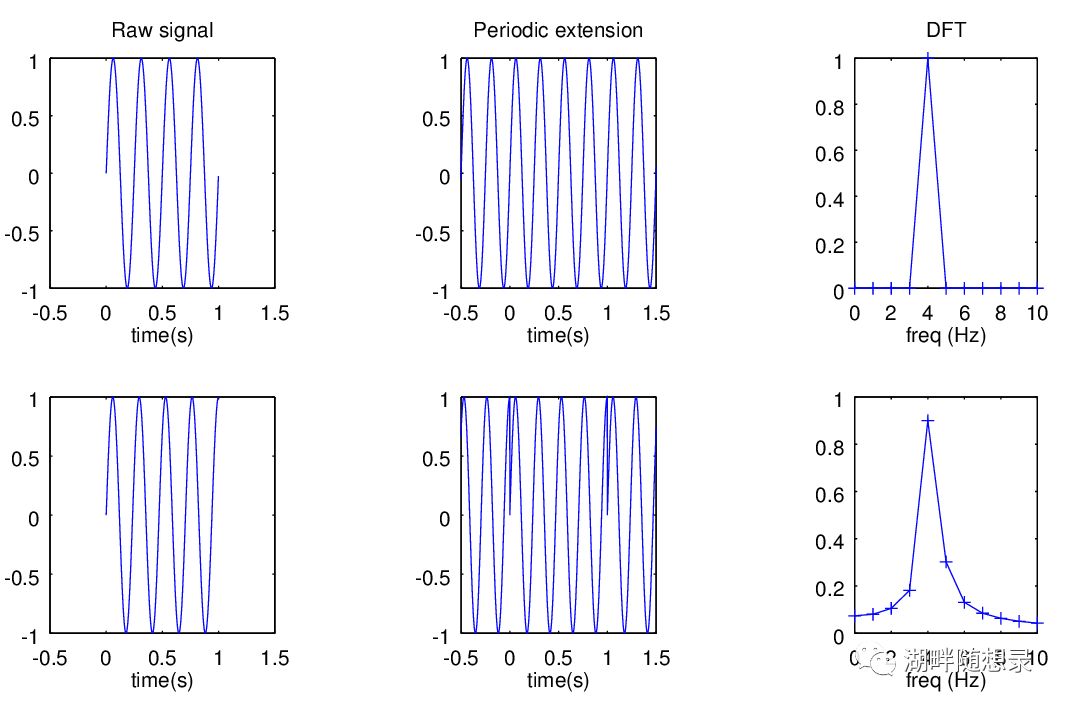
图3 频谱泄漏的产生
注意,如果正好是周期信号一个周期的延拓,那样是没有频谱泄漏的,理论上也不需要加窗。但实际工程应用中的信号过于复杂,不可能做到这一点,所以加窗就变成了一个标准操作。
加窗导致信号的能量发生了变化,想当于每个点乘以 sum_of_window / len_of_window,那么IFFT之后需要乘以 len_of_window / sum_of_window 把能量补偿回来。
线性卷积
一个线性时不变系统的输出就是输入信号和系统冲激响应的线性卷积。
线性卷积的公式是:
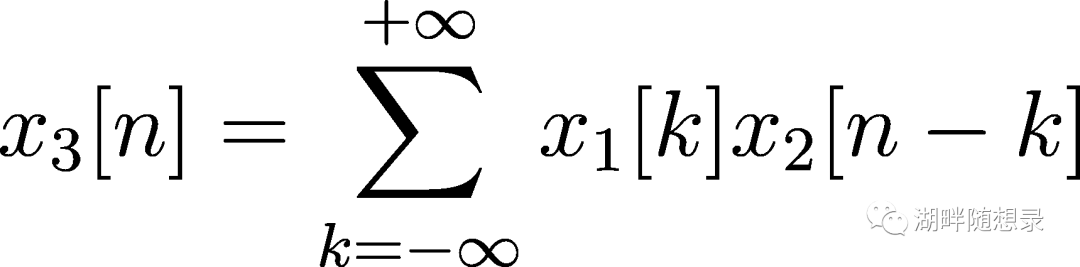
可见,加入x1的长度是N1,x2的长度是N2,那么x3的长度就是N1+N2-1。
但是因为FFT隐含的周期性,FFT的时域卷积是周期信号的线性卷积。而周期信号一旦卷积起来,就好像是按照周期N循环一样,所以称为循环卷积。
线性卷积的快速解法:
- 选取 N>=(N1+N2-1);
- 计算两个序列 x1[n] 和 x2[n] 的N点FFT X1[k] 和 X2[k];
- 计算乘积 X3[k]=X1[k]*X2[k];
- 计算 X3[k] 的IFFT逆变换得到 x1[n] 和 x2[n] 的循环卷积,由于N足够大,其实等于线性卷积。
但还有一种情况是实时的线性卷积,这种情况很常见,比如实时录制的音频流卷积一个滤波器,再实时的输出处理后的信号。我们也可以利用FFT来节省计算资源,但显然音频流的长度是不可知的,也就无法通过上面的方式进行计算。
但可以通过如下途径来“分段”循环卷积。
简单说明一下:h是滤波器系数,假如它的长度是L,则定义FFT的长度N=2L,在h的后面补零。in_data是输入数据,out_data是输出数据。长度为N的输入数据需要两步才能处理完成,每一步都需要做长度为N的FFT/IFFT,之后,丢弃生成的前N/2长度的数据,保留后面N/2长度的数据到输出缓冲区中。所以若产生N长度的数据,需要做两次N长度的FFT/IFFT。具体过程请参考图示进行推导。
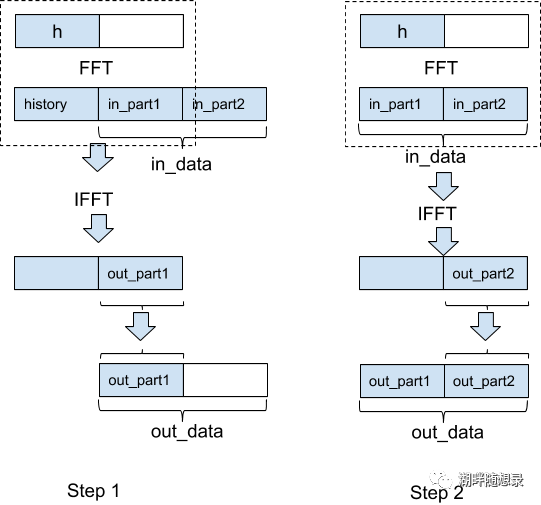
图4 分段循环卷积
-
FFT
+关注
关注
15文章
434浏览量
59370 -
信号处理器
+关注
关注
1文章
254浏览量
25272 -
频谱仪
+关注
关注
7文章
340浏览量
36035 -
傅里叶变换
+关注
关注
6文章
441浏览量
42595 -
DFS
+关注
关注
0文章
26浏览量
9162
发布评论请先 登录
相关推荐
快速傅里叶变换FFT结果的物理意义
【安富莱——DSP教程】第24章 快速傅里叶变换原理(FFT)
第24章 快速傅里叶变换原理(FFT)
如何在iMX8X arm处理器上利用GPU加速运算快速傅里叶变换FFT
快速傅里叶变换FFT结果的物理意义的程序详细说明





 快速傅里叶变换FFT原理
快速傅里叶变换FFT原理
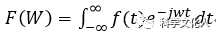










评论