粒子群算法(Particle Swarm Optimization,PSO)属于进化算法的一种,和模拟退火算法相似,它也是从随机解出发,通过迭代寻找最优解。它也是通过适应度来评价解的品质,但它比遗传算法规则更为简单,没有遗传算法的“交叉”(Crossover)和“变异”(Mutation)操作,它通过追随当前搜索到的最优值来寻找全局最优。
**10.1.1 **基本原理
PSO可以用于解决优化问题。在PSO中,每个优化问题的潜在解都是搜索空间中的一只鸟,称为粒子。所有的粒子都有一个由被优化的函数决定的适值(Fitness Value),每个粒子还有一个速度决定它们“飞行”的方向和距离。然后粒子们就追随当前的最优粒子在解空间中搜索。
粒子位置的更新方式如图10-1所示。
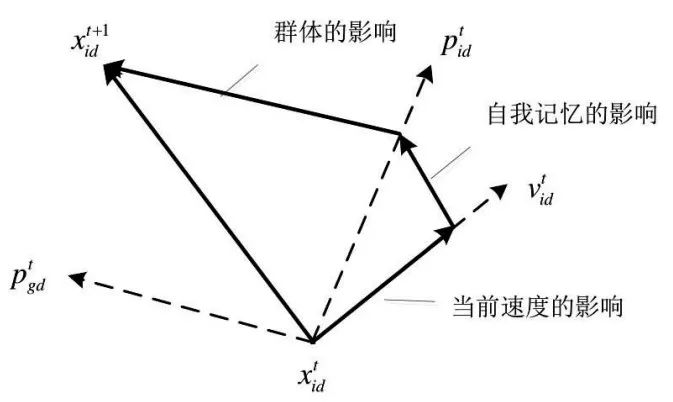
图10-1 粒子位置的更新方式
其中,x表示粒子起始位置,v表示粒子“飞行”的速度,p表示搜索到的粒子的最优位置。
PSO初始化为一群随机粒子(随机解),然后通过迭代找到最优解。在每一次迭代中,粒子通过跟踪两个极值来更新自己:一个是粒子本身所找到的最优解,这个解称为个体极值;另一个极值是整个种群目前找到的最优解,这个极值是全局极值。
另外,也可以不用整个种群而只用其中一部分作为粒子的邻居,那么在所有邻居中的极值就是局部极值。
假设在一个D维的目标搜索空间中,有N个粒子组成一个群落,其中第i个粒子表示为一个D维的向量
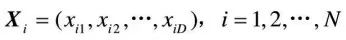
第i个粒子的“飞行”速度也是一个D维的向量,记为
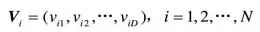
第i个粒子迄今为止搜索到的最优位置称为个体极值,记为
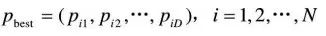
整个粒子群迄今为止搜索到的最优位置为全局极值,记为
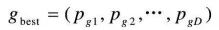
在找到这两个最优值时,粒子根据如下公式来更新自己的速度和位置:
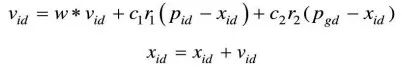
其中,c1和c2为学习因子,也称加速常数(Acceleration Constant);r1和r2为[0,1]范围内的均匀随机数。
式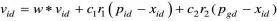 右边由三部分组成:
右边由三部分组成:
● 第一部分为“惯性”(Inertia)或“动量”(Momentum)部分,反映了粒子的运动“习惯(Habit)”,代表粒子有维持自己先前速度的趋势。
● 第二部分为“认知”(Cognition)部分,反映了粒子对自身历史经验的记忆或回忆,代表粒子有向自身历史最佳位置逼近的趋势。
● 第三部分为“社会”(Social)部分,反映了粒子间协同合作与知识共享的群体历史经验,代表粒子有向群体或邻域历史最佳位置逼近的趋势。
由于粒子群算法具有高效的搜索能力,因此有利于得到多目标意义下的最优解;通过代表整个解集种群,按并行方式同时搜索多个非劣解,即搜索到多个Pareto最优解。
同时,粒子群算法的通用性比较好,适合处理多种类型的目标函数和约束,并且容易与传统的优化方法结合,从而改进自身的局限性,更高效地解决问题。因此,将粒子群算法应用于解决多目标优化问题上具有很大的优势。
**10.1.2 **程序设计
基本粒子群算法的流程图如图10-2所示。其具体过程如下:
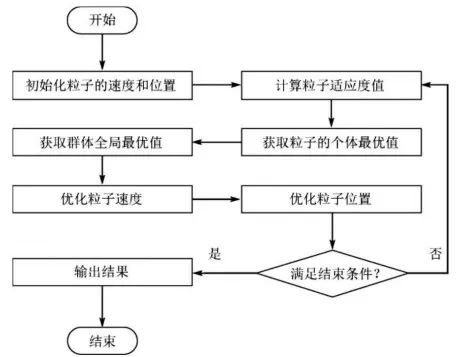
图10-2 基本粒子群算法流程图
① 初始化粒子群,包括群体规模N、每个粒子的位置xi和速度v i 。
② 计算每个粒子的适应度值F it [i]。
③ 对每个粒子,用它的适应度值F it [i]和个体极值p best (i)比较,如果F it [i] > p best (i),则用F it [i]替换p best (i)。
④ 对每个粒子,用它的适应度值F it [i]和个体极值g best (i)比较,如果F it [i] > p best (i),则用F it [i]替换g best (i)。
⑤ 更新粒子的速度vi和位置x i 。
⑥ 如果满足结束条件(误差足够好或达到最大循环次数)则退出,否则返回②。
在MATLAB中编程实现的基本粒子群算法基本函数为PSO,其调用格式如下:
[xm, fv] = PSO(fitness, N, c1, c2, w, M, D)
其中,fitness为待优化的目标函数,也称适应度函数。N是粒子数目,c1是学习因子1,c2是学习因子2,w是惯性权重,M是最大迭代次数,D是自变量的个数,xm是目标函数取最小值时的自变量,fv是目标函数的最小值。
使用MATLAB实现基本粒子群算法代码如下:
function [xm, fv] = PSO(fitness, N, c1, c2, w, M, D)
%%%%% 给定初始化条件 %%%%%%
% c1学习因子1
% c2学习因子2
% w惯性权重
% M最大迭代次数
% D搜索空间维数
% N初始化群体个数数目
%%%%%% 初始化种群的个体(可以在这里限定位置和速度的范围) %%%%%%
format long;
for i = 1 : N
for j = 1 : D
x(i, j) = randn; % 随机初始化位置
v(i, j) = randn; % 随机初始化速度
end
end
%%%%%% 先计算各个粒子的适应度,并初始化Pi和Pg %%%%%%
for i = 1 : N
p(i) = fitness(x(i, :));
y(i, :) = x(i, :);
end
pg = x(N, :); %Pg为全局最优
for i = 1 : (N - 1)
if fitness(x(i, :)) < fitness(pg)
pg = x(i, :);
end
end
%%%%%% 进入主要循环,按照公式依次迭代,直到满足精度要求 %%%%%%
for t = 1 : M
for i = 1 : N % 更新速度、位移
v(i, :) = w * v(i, :) + c1 * rand * (y(i, :) - x(i, :)) + c2 * rand * (pg - x(i, :));
x(i, :) = x(i, :) + v(i, :);
if fitness(x(i, :)) < p(i)
p(i) = fitness(x(i, :));
y(i, :) = x(i, :);
end
if p(i) < fitness(pg)
pg = y(i, :);
end
end
Pbest(t) = fitness(pg);
end
%%%%%% 最终给出计算结果 %%%%%%
disp('*************************************************')
disp('目标函数取最小值时的自变量:')
xm = pg'
disp('目标函数的最小值为:')
fv = fitness(pg)
disp('*************************************************')
将上面的函数保存到MATLAB可搜索路径中,即可调用该函数。再定义不同的目标函数fitness和其他输入量,就可以用粒子群算法求解不同问题。
粒子群算法使用的函数有很多个,下面介绍两个常用的适应度函数。
1.Griewank函数
Griewank函数的MATLAB代码如下:
function y = Griewank(x) % Griewank函数
% 输入x,给定相应的y值,在x = (0, 0, ……, 0)处有全局极小点0
[row, col] = size(x);
if row > 1
error('输入的参数错误');
end
y1 = 1 / 4000 * sum(x .^ 2);
y2 = 1;
for h = 1 : col
y2 = y2 * cos(x(h) / sqrt(h));
end
y = y1 - y2 + 1;
y = - y;
绘制以上函数图像的MATLAB代码如下:
function DrawGriewank() % 绘制Griewank函数图像
x = [-8 : 0.1 : 8];
y = x;
[X, Y] = meshgrid(x, y);
[row, col] = size(X);
for l = 1 : col
for h = l : row
z(h, l) = Griewank([X(h, l), Y(h, l)]);
end
end
surf(X, Y, z);
shading interp
将以上代码保存为DrawGriewank.m文件,并运行上述代码,得到Griewank函数图像,如图10-3所示。
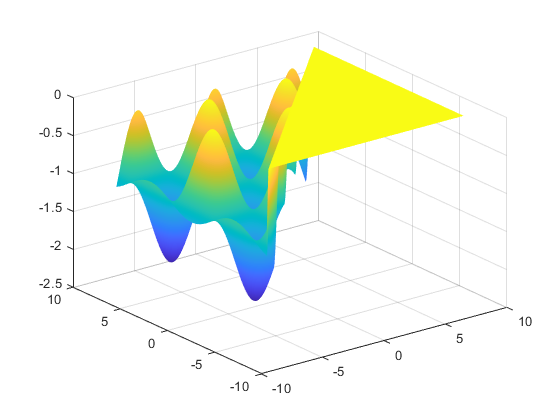
图10-3 Griewank函数图像
2.Rastrigin函数
Rastrigin函数的MATLAB代码如下:
function y = Rastrigin(x) % Rastrigin函数
% 输入x,给定相应的y值,在x = (0, 0, ……, 0)处有全局极小点0
[row, col] = size(x);
if row > 1
error('输入的参数错误');
end
y = sum(x .^ 2 - 10 * cos(2 * pi * x) + 10);
y = - y;
绘制以上函数图像的MATLAB代码如下:
function DrawRastrigin()
x = [-4 : 0.05 : 4];
y = x;
[X, Y] = meshgrid(x, y);
[row, col] = size(X);
for l = 1 : col
for h = 1 : row
z(h, l) = Rastrigin([X(h, l), Y(h, l)]);
end
end
surf(X, Y, z);
shading interp
将以上代码保存为DrawRastrigin.m文件,并运行上述代码,得到Rastrigin函数图像,如图10-4所示。
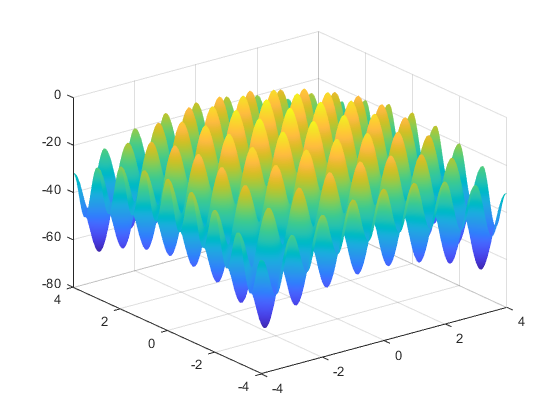
图10-4 Rastrigin函数图像
例10-1:利用上文介绍的基本粒子群算法求解下列函数的最小值。
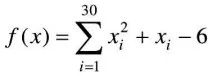
利用基本粒子群算法求解最小值,首先需要确认不同迭代步数对结果的影响。设定题中函数的最小点均为0,粒子群规模为50,惯性权重为0.5,学习因子c1为1.5,学习因子c2为2.5,迭代步数分别取100、1000、10000。
在MATLAB中建立目标函数代码,并保存为fitness.m文件:
function F = fitness(x)
F = 0;
for i = 1 : 30
F = F + x(i)^2 + x(i) - 6
end
在MATLAB命令行窗口中依次输入:
x = zeros(1, 30);
[xm1, fv1] = PSO(@fitness, 50, 1.5, 2.5, 0.5, 100, 30);
[xm2, fv2] = PSO(@fitness, 50, 1.5, 2.5, 0.5, 1000, 30);
[xm3, fv3] = PSO(@fitness, 50, 1.5, 2.5, 0.5, 10000, 30);
运行以上代码,比较目标函数取最小值时的自变量,如表10-1所示。
表10-1 比较不同迭代步数下的目标函数值和最小值
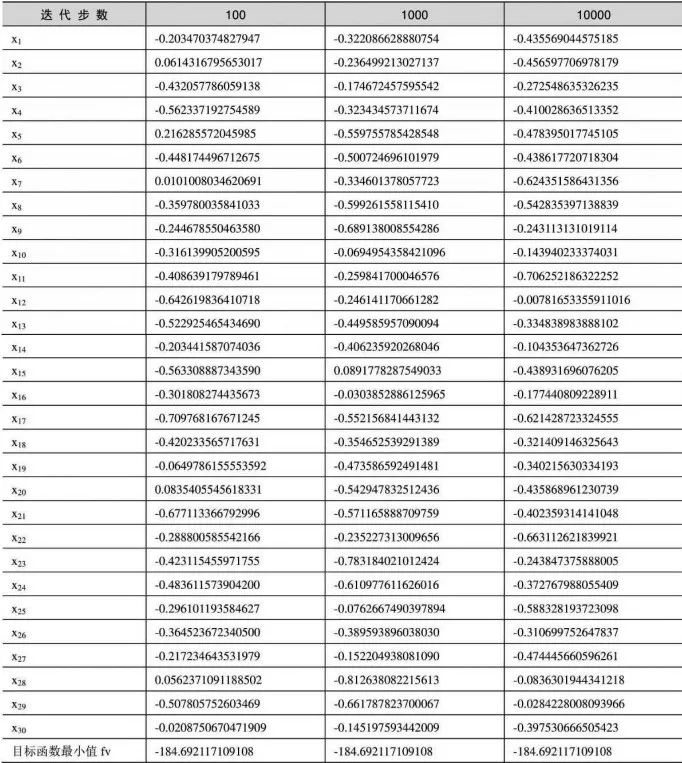
从表10-1中可以看出,迭代步数不一定与获得解的精度成正比,即迭代步数越大,获得解的精度不一定越高。这是因为粒子群算法是一种随机算法,同样的参数也会算出不同的结果。
在上述参数的基础上,保持惯性权重为0.5、学习因子c1为1.5、学习因子c2为2.5、迭代步数为100不变,粒子群规模分别取10、100和500,运行以下MATLAB代码:
x = zeros(1, 30);
[xm1, fv1] = PSO(@fitness, 10, 1.5, 2.5, 0.5, 100, 30);
[xm2, fv2] = PSO(@fitness, 100, 1.5, 2.5, 0.5, 100, 30);
[xm3, fv3] = PSO(@fitness, 500, 1.5, 2.5, 0.5, 100, 30);
比较目标函数取最小值时的自变量,如表10-2所示。
表10-2 比较不同粒子群规模下的目标函数值和最小值
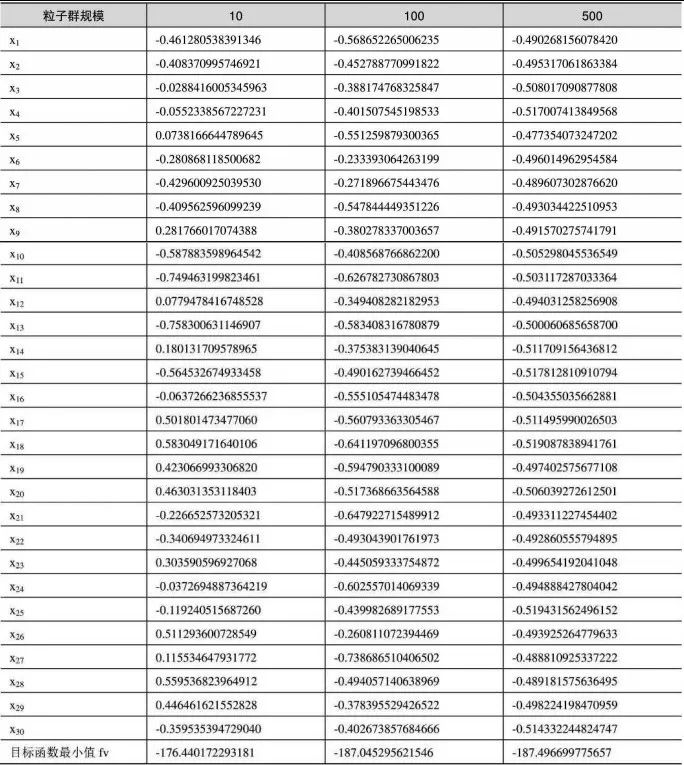
从表10-2中可以看出,粒子群规模越大,获得解的精度不一定越高。
综合以上不同迭代步数和不同粒子群规模运算得到的结果可知,在粒子群算法中,要想获得精度高的解,关键是各个参数之间的匹配。
-
人工智能
+关注
关注
1796文章
47643浏览量
239940 -
MATLAB仿真
+关注
关注
4文章
176浏览量
19982 -
PSO
+关注
关注
0文章
49浏览量
12964 -
粒子群算法
+关注
关注
0文章
63浏览量
13085 -
机器学习
+关注
关注
66文章
8438浏览量
132998
发布评论请先 登录
相关推荐
基于粒子群算法的自适应LMS滤波器设计及可重构硬件实现
【Simulink】粒子群算法(PSO)整定PID参数(附代码和讲解)精选资料分享
基于matlab粒子群配电网重构简介
简化的位置随机扰动粒子群算法
一种共享并行粒子群算法
如何使用免疫粒子群优化算法实现增量式的PID控制
【优化选址】基于模拟退火结合粒子群算法求解分布式电源定容选址问题matlab源码





 粒子群算法的MATLAB实现(1)
粒子群算法的MATLAB实现(1)
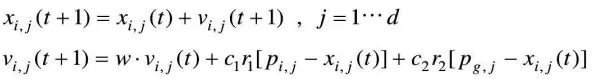










评论