**10.1.3 **经典应用
粒子群算法经常与其他算法混合使用。混合策略就是将其他进化算法、传统优化算法或其他技术应用到PSO中,用于提高粒子多样性、增强粒子的全局探索能力,或者提高局部开发能力、增强收敛速度与精度。
常用的粒子群混合方法基于免疫的粒子群算法。该算法是在免疫算法的基础上采用粒子群优化对抗体群体进行更新,可以解决免疫算法收敛速度慢的缺点。
基于免疫的混合粒子群算法步骤如下所示。
① 确定学习因子c1和c 2 、粒子(抗体)群体个数M。
② 由logistic回归分析映射产生M个粒子(抗体)xi及其速度v i ,其中i=1,…,N,最后形成初始粒子(抗体)群体P 0 。
③ 产生免疫记忆粒子(抗体):计算当前粒子(抗体)群体P中粒子(抗体)的适应度值并判断算法是否满足结束条件,如果满足则结束并输出结果,否则继续运行。
④ 更新局部和全局最优解,并根据下面的公式更新粒子位置和速度。
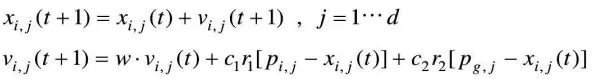
⑤ 由logistic映射产生N个新的粒子(抗体)。
⑥ 基于浓度的粒子(抗体)选择:用群体中相似抗体百分比计算产生N + M个新粒子(抗体)的概率,依照概率大小选择N个粒子(抗体)形成粒子(抗体)群体P。然后转入第③步。
算法流程图如图10-5所示。
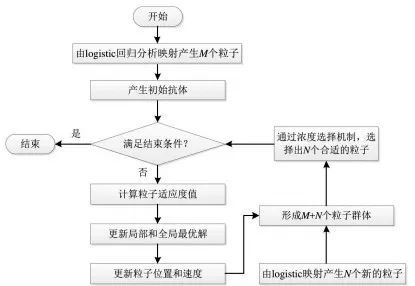
图10-5 免疫粒子群算法流程图
将实现自适应权重的优化函数命名为PSO_immu.m,在MATLAB中编写实现以上步骤的代码:
function [x, y, Result] = PSO_immu(func, N, c1, c2, w, MaxDT, D, eps, DS, replaceP, minD, Psum)
format long;
%%%%%% 给定初始化条件 %%%%%%
% c1 = 2; % 学习因子1
% c2 = 2; % 学习因子2
% w = 0.8; % 惯性权重
% MaxDT = 100; % 最大迭代次数
% D = 2; % 搜索空间维数(未知数个数)
% N = 100; % 初始化群体个体数目
% eps = 10^(-10); % 设置精度(在已知最小值时用)
% DS = 8; % 每隔DS次循环就检查最优个体是否变优
% replaceP = 0. 5; % 粒子的概率大于replaceP将被免疫替换
% minD = 1e-10; % 粒子间的最小距离
% Psum = 0; % 个体最佳的和
range = 100;
count = 0;
%%%%%% 初始化种群的个体 %%%%%%
for i = 1 : N
for j = 1 : D
x(i,j) = -range + 2 * range * rand; %随机初始化位置
v(i,j) = randn; % 随机初始化速度
end
end
%%%%%% 先计算各个粒子的适应度,并初始化Pi和 Pg %%%%%%
for i = 1 : N
p(i) = feval(func,x(i, : ));
y(i, :) = x(i, :);
end
pg = x(1, :); % Pg为全局最优
for i = 2 : N
if feval(func, x(i, :)) < feval(func, pg)
pg = x(i, :);
end
end
%%%%%% 主循环,按照公式依次迭代,直到满足精度要求 %%%%%%
for t = 1 : MaxDT
for i = 1 : N
v(i, :) = w * v(i, :) + c1 * rand * (y(i, :) - x(i, :) ) + c2 * rand * (pg - x (i, :));
x(i, :) = x(i, :) + v(i, :);
if feval(func,x(i, :)) < p(i)
p(i) = feval(func, x(i, :));
y(i, :) = x(i, :);
end
if p(i) < feval(func, pg)
pg = y(i, :);
subplot(1, 2, 1);
bar(pg, 0.25);
axis( [0 3 -40 40]);
title ( [ 'Iteration', num2str(t)]); pause(0.1);
subplot(1, 2, 2);
plot(pg(1, 1), pg(1, 2), 'rs', 'MarkerFacecolor', 'r', 'Markersize', 8)
hold on;
plot(x(:, 1),x(:, 2), 'k.');
set(gca, 'Color', 'g')
hold off;
grid on;
axis([-100 100 -100 100]);
title(['Global Min = ' , num2str(p(i))]);
xlabel(['Min_x= ', num2str(pg(1, 1)), 'Min_y= ', num2str(pg(1, 2))]);
end
end
Pbest(t) = feval(func, pg);
% if Foxhole(pg,D)
% break;
% end
%%%%%% 开始进行免疫 %%%%%%
if t > DS
if (mod(t, DS) == 0) && ((Pbest(t - DS + 1) - Pbest(t)) < 1e-020)
% 如果连续DS代数,群体中的最优没有明显变优,则进行免疫
% 在函数测试的过程中发现,经过一定代数的更新,个体最优不完全相等,但变化极小
for i = 1 : N % 先计算出个体最优的和
Psum = Psum + p(i);
end
for i = 1 : N % 免疫程序
for j = 1 : N % 计算每个个体与个体i的距离
distance(j) = abs(p(j)-p(i));
end
num = 0;
for j = 1 : N % 计算与第i个个体距离小于minD的个数
if distance(j) < minD
num = num + 1;
end
end
PF(i) = p(N - i + 1) / Psum; % 计算适应度概率
PD(i) = num / N; % 计算个体浓度
a=rand; % 随机生成计算替换概率的因子
PR(i) = a * PF(i) + (1 - a) * PD(i); % 计算替换概率
end
for i = 1 : N
if PR(i) > replaceP
x(i, :) = -range + 2 * range * rand(1, D);
count=count+1;
end
end
end
end
end
%%%%%% 最后给出计算结果 %%%%%%
x = pg(1, 1);
y = pg(1, 2);
Result = feval(func, pg);
%%%%%% 算法结束 %%%%%%
function probabolity(N, i)
PF = p(N - i) / Psum; % 适应度概率
disp(PF);
for jj = 1 : N
distance(jj) = abs(P(jj)-P(i));
end
num = 0;
for ii = 1 : N
if distance(ii) < minD
num = num + 1;
end
end
PD = num/N; % 个体浓度
PR = a * PF + (1 - a) * PD; % 替换概率
例10-2:使用基于模拟退火的混合粒子群算法,求解函数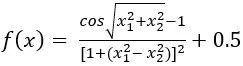 的最小值。其中-10≤ x
的最小值。其中-10≤ xi ≤10,粒子数为50,学习因子均为2,退火常数取0.6,迭代步数为1000。
首先建立目标函数代码:
function y = immuFunc(x)
y = (cos(x(1)^2 + x(2)^2) - 1)/((1 + (x(1)^2 - x(2)^2))^2) + 0.5;
end
在MATLAB命令行窗口中输入代码:
[xm, fv] = PSO_immu(@immuFunc, 50, 2, 2, 0.8, 100, 5, 0.0000001, 10, 0.6, 0.0000000000000000001, 0)
运行结果如下:
xm =
-0.735230545314342
fv =
1.241562924919382
得到目标函数取最小值时的自变量xm变化图,如图10-6所示。
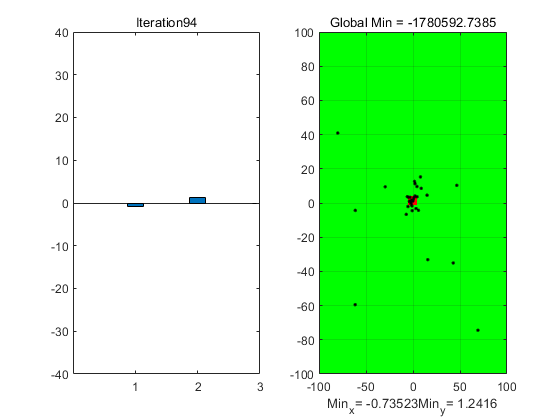
图10-6 目标函数取最小值时的自变量xm变化图
-
MATLAB仿真
+关注
关注
4文章
176浏览量
19931 -
PSO
+关注
关注
0文章
49浏览量
12944 -
粒子群算法
+关注
关注
0文章
63浏览量
13053
发布评论请先 登录
相关推荐
基于粒子群算法的自适应LMS滤波器设计及可重构硬件实现
粒子群算法城镇能源优化调度问题
什么是粒子群算法?
【Simulink】粒子群算法(PSO)整定PID参数(附代码和讲解)精选资料分享
基于matlab粒子群配电网重构简介
简化的位置随机扰动粒子群算法
一种共享并行粒子群算法
如何使用免疫粒子群优化算法实现增量式的PID控制
【优化选址】基于模拟退火结合粒子群算法求解分布式电源定容选址问题matlab源码





 粒子群算法的MATLAB实现(2)
粒子群算法的MATLAB实现(2)










评论