正文

然后看到这篇关于浮点数的文章,希望大家看了之后有所启发。
想一下,为什么第一个打印的和预设值不同,但是第二个是相同的?
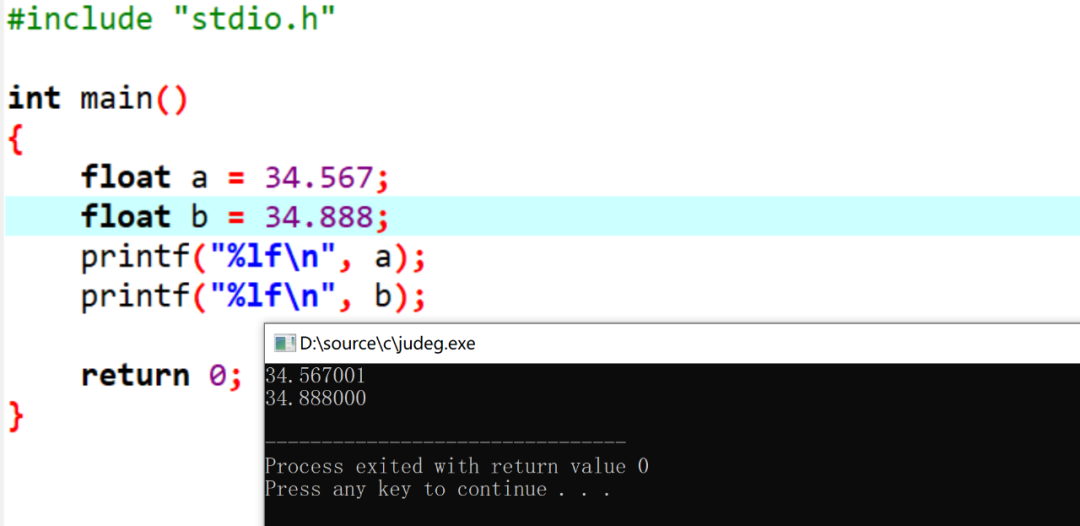
如图:
尾数部分是如何转变成二进制的?

前言
很多人在初学写程式时都会遇到所谓的浮点误差,如果你到目前都还没被浮点误差雷过,那只能说你真的很幸运XD。
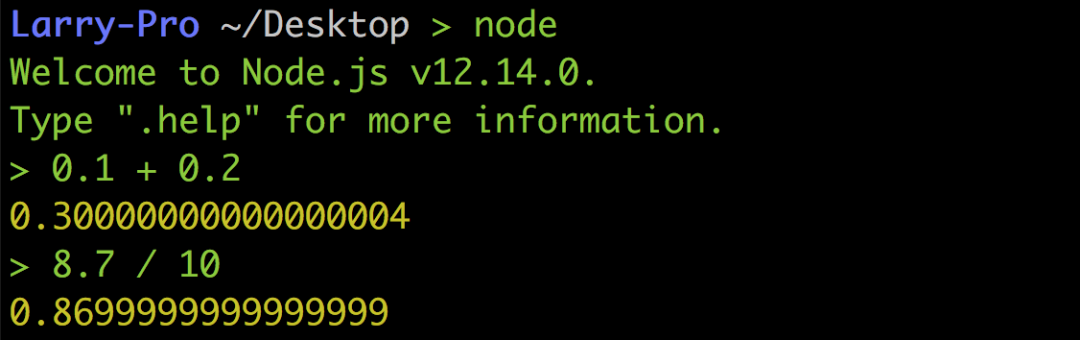
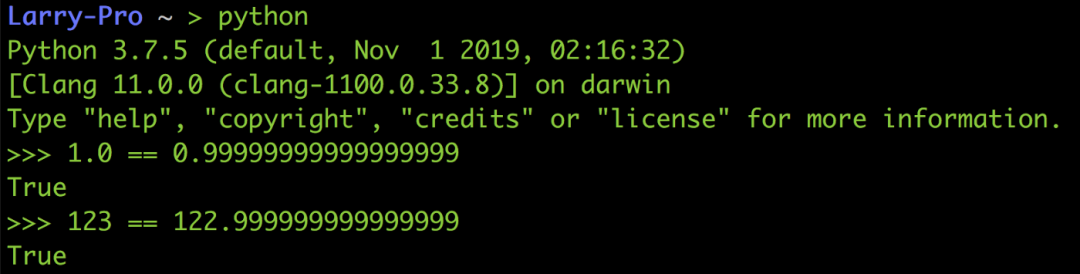
以下图Python 的例子来说0.1 + 0.2并不等于0.3,8.7 / 10也不等于0.87,而是0.869999…,真的超怪der

但这绝对不是什么神bug,也不是Python 设计得不好,而是浮点数在做运算时必然的结果,所以即便是到了Node.js 或其他语言也都是一样。
电脑如何储存一个整数(Integer)
在讲为什么会有浮点误差之前,先来谈谈电脑是怎么用0 跟1 来表示一个整数,大家应该都知道二进制这个东西:像101代表2² + 2⁰ 也就是5、1010代表2³ + 2¹ 也就是10。
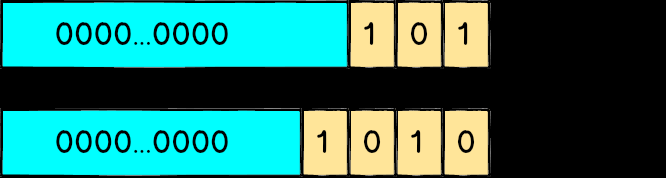
如果是一个unsigned 的32 bit 整数,代表他有32 个位置可以放0 或1,所以最小值就是0000...0000也就是0,而最大值1111...1111代表2³¹ + 2³⁰ + … + 2¹ + 2⁰ 也就是4294967295。
从排列组合的角度来想,因为每一个bit 都可以是0 或1,整个变数值有2³² 种可能性,所以可以精确的表达出0 到2³²-1 中任一个值,不会有任何误差。
浮点数(Floating Point)
虽然从0 到2³²-1 之间有很多很多个整数,但数量终究是有限的,就是2³² 个那么多而已;但浮点数就大大的不同了,大家可以这样想:在1 到10 这个区间中只有十个整数,但却有无限多个浮点数,譬如说5.1、5.11、5.111 等等,再怎么数都数不完。
但因为在32 bit 的空间中就只有2³² 种可能性,为了把所有浮点数都塞在这个32 bit 的空间里面,许多CPU 厂商发明了各种浮点数的表示方式,但若各家CPU 的格式都不一样也很麻烦,所以最后是以IEEE发布的IEEE 754作为通用的浮点数运算标准,后来的CPU 也都遵循这个标准进行设计。
IEEE 754
IEEE 754 里面定义了很多东西,其中包括单精度(32 bit)、双精度(64 bit)跟特殊值(无穷大、NaN)的表示方式等。
正规化
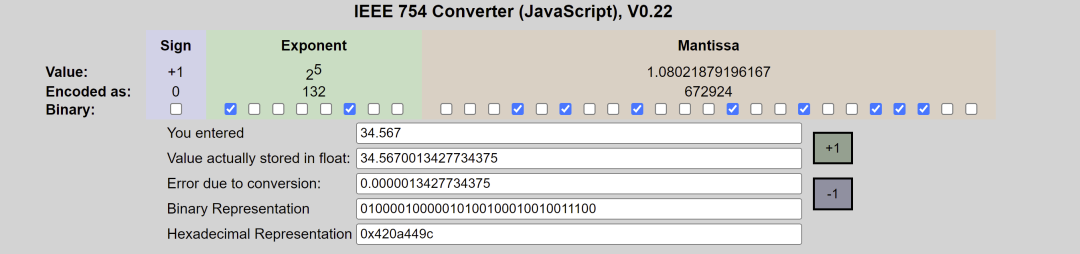
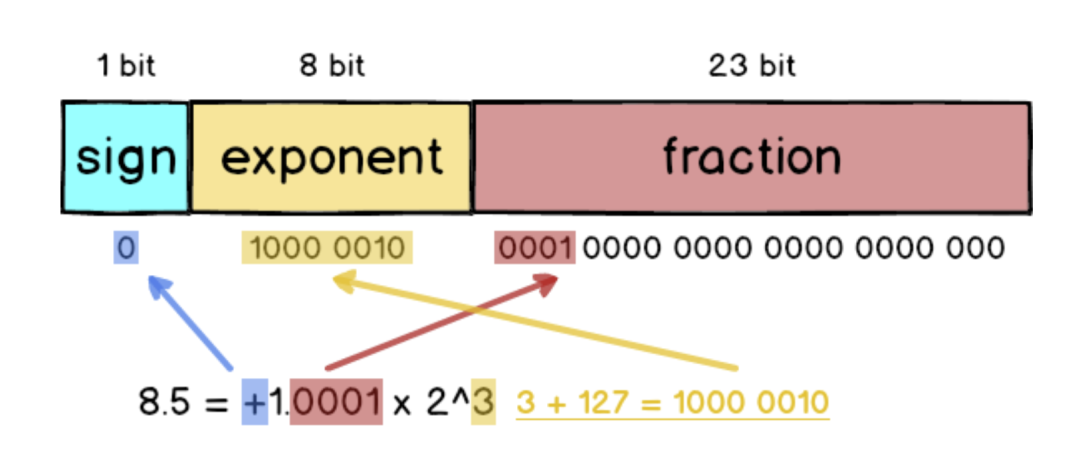
以8.5 这个符点数来说,如果要变成IEEE 754 格式的话必须先做正规化:把8.5 拆成8 + 0.5 也就是2³ + 1/2¹,接着写成二进位变成1000.1,最后再写成1.0001 x 2³,跟十进位的科学记号满像的。
单精度浮点数
在IEEE 754 中32 bit 浮点数被拆成三个部分,分别是sign、exponent 跟fraction,加起来总共是32 个bit。
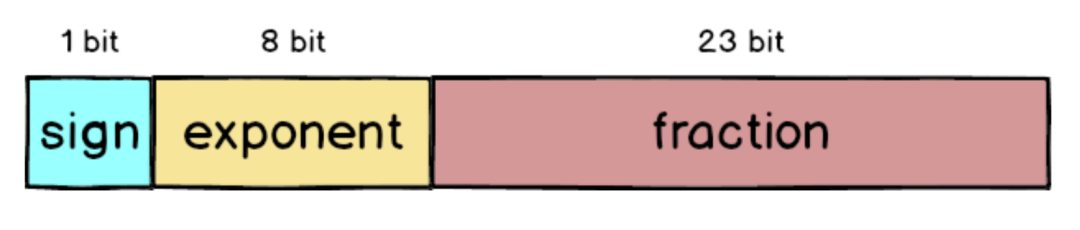
sign:最左侧的1 bit 代表正负号,正数的话sign 就为0,反之则是 1。
exponent:中间的8 bit 代表正规化后的次方数,采用的是超127格式,也就是3 还要加上127 = 130。
fraction:最右侧的23 bit 放的是小数部分,以1.0001 来说就是去掉1. 之后的000。
所以如果把8.5 表示成32 bit 格式的话就会是这样:
这图我画超久的,请大家仔细看XD。
什么情况下会不准呢?
刚刚8.5 的例子可以完全表示为2³+ 1/2¹,是因为8 跟0.5 刚好都是2 的次方数,所以完全不需要牺牲任何精准度。
但如果是8.9 的话因为没办法换成2 的次方数相加,所以最后会被迫表示成1.0001110011… x 2³,而且还会产生大概0.0000003 的误差,好奇结果的话可以到IEEE-754 Floating Point Converter网站上玩玩看。
双精度浮点数
上面讲的单精度浮点数只用了32 bit 来表示,为了让误差更小,IEEE 754 也定义了如何用64 bit 来表示浮点数,跟32 bit 比起来fraction 部分大了超过两倍,从23 bit 变成52 bit,所以精准度自然提高许多。
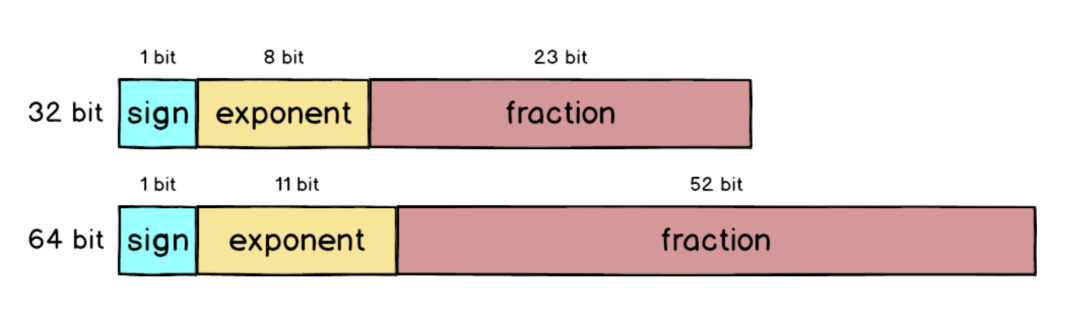
以刚刚不太准的8.9 为例,用64 bit 表示的话虽然可以变得更准,但因为8.9 无法完全写成2 的次方数相加,到了小数下16 位还是出现误差,不过跟原本的误差0.0000003 比起来已经小了很多。

类似的情况还有像Python 中的1.0跟0.999...999是相等的、123跟122.999...999也是相等的,因为他们之间的差距已经小到无法放在fraction 里面,所以就二进制的格式看来他们每一个bit 都一样。
解决方法
既然无法避免浮点误差,那就只好跟他共处了(打不过就加入?),这边提供两个比较常见的处理方法。
设定最大允许误差ε (epsilon)
在某些语言里面会提供所谓的epsilon,用来让你判断是不是在浮点误差的允许范围内,以Python 来说epsilon 的值大概是2.2e-16。
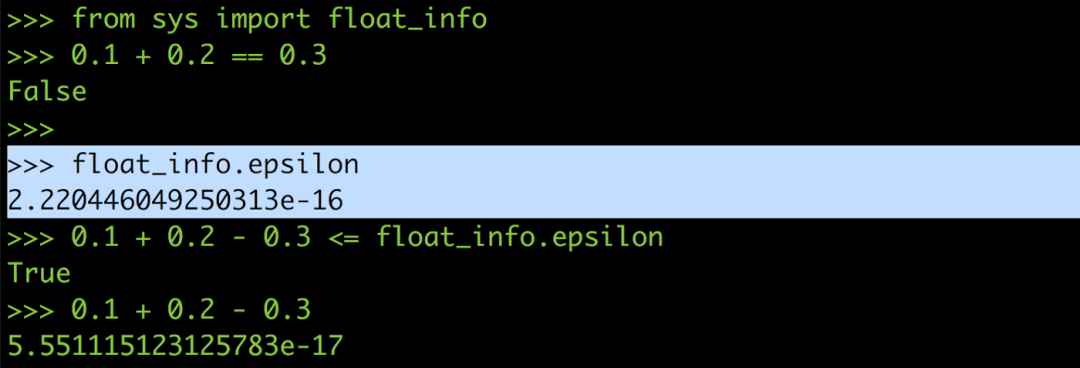
所以你可以把0.1 + 0.2 == 0.3改写成0.1 + 0.2 — 0.3 <= epsilon,这样就能避免浮点误差在运算过程中作怪,也就可以正确比较出0.1 加0.2 是不是等于0.3。
当然如果系统没提供的话你也可以自己定义一个epsilon,设定在2 的-15 次方左右。
完全使用十进位进行计算
之所以会有浮点误差,是因为十进制转二进制的过程中没办法把所有的小数部分都塞进fraction,既然转换可能会有误差,那干脆就不要转了,直接用十进制来做计算!!
在Python 里面有一个module 叫做decimal,它可以帮你用十进位来进行计算,就像你自己用纸笔计算0.1 + 0.2 绝对不会出错、也不会有任何误差(其他语言也有类似的模组)。
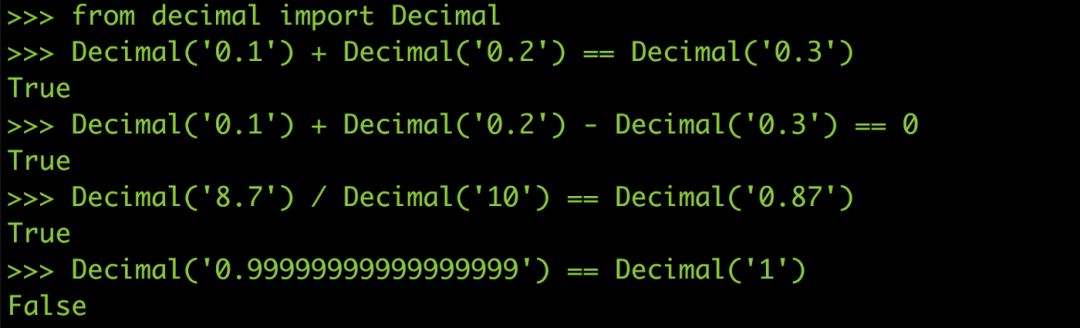
自从我用了Decimal 之后不只bug 不见了,连考试也都考一百分了呢!
虽然用十进位进行计算可以完全躲掉浮点误差,但因为Decimal 的十进位计算是模拟出来的,在最底层的CPU 电路中还是用二进位在进行计算,所以跑起来会比原生的浮点运算慢非常多,所以也不建议全部的浮点运算都用Decimal 来做。
总结
回归到这篇文章的主题:「为什么浮点误差是无法避免的?」,相信大家都已经知道了。
至于你说知道IEEE 754 的浮点数格式有什么用吗?好像也没什么特别的用处XD,只是觉得能从浮点数的格式来探究误差的成因很有趣而已,感觉离真相又近了一点点。
而且说不定哪天会有人问我「为什么浮点运算会产生误差而整数不会」,那时我就可以有自信的讲解给他听,而不是跟他说「反正浮点运算就是会有误差,背起来就对了」
来源:https://medium.com/starbugs/see-why-floating-point-error-can-not-be-avoided-from-ieee-754-809720b32175 版权归原作者或平台所有,仅供学习参考与学术研究,如有侵权,麻烦联系删除~感谢
审核编辑:刘清
-
二进制
+关注
关注
2文章
794浏览量
41637 -
python
+关注
关注
56文章
4792浏览量
84614
原文标题:为什么浮点运算会产生误差而整数不会?
文章出处:【微信号:最后一个bug,微信公众号:最后一个bug】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
二进制格雷码与自然二进制码的互换分析
二进制数逻辑运算是怎么运算的
浮点数转换为二进制存储的方法
二进制电平,什么是二进制电平
浮点数转换为二进制存储





 浮点运算的尾数部分是如何转变成二进制的?
浮点运算的尾数部分是如何转变成二进制的?











评论