人工神经网络（梯度下降算法）介绍

在实际问题中，已知量是数据和数据标签，决策函数是未知的，即神经网络的结构未知。

因此，在使用人工神经网络结构解决实际问题时，需先假设人工神经网络结构，再将训练数据输入到该结构中 ，最后求解待求参数。

一、假设人工神经网络结构

假设人工神经网络结构主要需要确定两个问题：

（1）人工神经网络结构共有多少层？

（2）每层神经元的数量是多少？

目前，上述两个问题没有标准答案，开发人员需根据经验解决上述两个问题。解决上述两个问题时，开发人员可根据以下准则：

（1）若问题是简单的，两个类别的分界曲线是不复杂的，则可选用较简单的人工神经网络结构，即人工神经网络层数和每层神经数量均可较少。



图片来源：中国慕课大学《机器学习概论》

（2）若问题是复杂的，例如：人脸识别问题，则可选用较复杂的人工神经网络结构，即人工神经网络层数和每层神经数量均可较多。

（3）若训练数据较少，则可选用较简单的人工神经网络结构。

（4）若训练数据较多，则可选用较复杂的人工神经网络结构。

二、求解人工神经网络待求参数

以两层神经网络模型为例，如图一所示，输入为(X,Y)，其中，X=[x1,x2]T，Y是标签值（label），问题为通过改变ω和b的值，使得标签值Y与实际的人工神经网络输出值y最接近。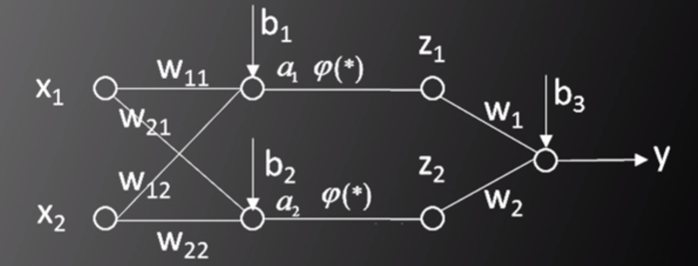



图一，图片来源：中国慕课大学《机器学习概论》

根据前篇文章，y的表达式为： y=ω1φ(ω11x1+ω12x2+b1)+ω2φ(ω21x1+ω22x2+b1)+b3

使得y和Y最接近可表达为： Minimize:E(ω,b)=E(X,Y)[(Y-y)2]

其中，E(X,Y)为训练样本和标签的数学期望（平均值）。因为y是(ω,b)的非凸函数，所以该问题无法求得唯一最小值。

因此，采用梯度下降法(Gradient Descent Method)求解局部极小值。梯度下降法的步骤如下：

（1）随机选取ω和b的初始值(ω(0),b(0))

（2）应用迭代算法求目标函数的局部极值，在第n步迭代中，ω和b的迭代公式为： ω(n+1)=ω(n)-α·∂E/∂ω b(n+1)=b(n)-α·∂E/∂b

其中，α为学习率（Learning rate），α由开发人员设定，开发人员需选取合适的α值，若α值被设定得过大，则容易错过局部极值点，若α值被设定得过小，则可能较长时间不能找到局部极值点，只有当α值被设定得合适时，才能快速收敛至局部极值点。但因为人工神经网络对应的决策函数未知，所以没有一种可求解α值的方法，开发人员需根据经验设定α值。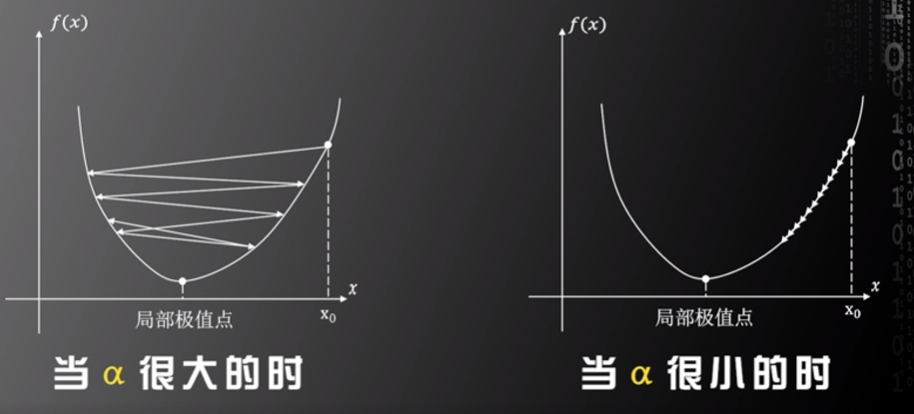



图片来源：中国慕课大学《机器学习概论》

梯度下降法的含义：如图二所示，通过迭代的方式逐步遍历x1，x2，x3，…，xn，最终找到函数的局部极小值，此值即为y和Y最接近的值。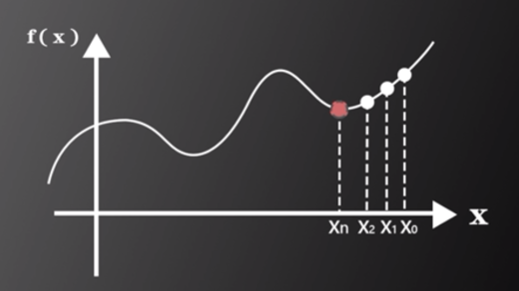



图片来源：中国慕课大学《机器学习概论》

审核编辑：刘清