为什么 sin(x²)+sin(y²)=1 的图像这么复杂？

其原因有两条：一是看似简单的数学公式可以生成十分复杂的图像图形，二是看似十分复杂的图像图形可以由简单的数学公式实现。 显然这两句话是一个意思，也并没有什么营养。

最初我以为笑话里讲的“数字里添加的字母”是代数里用的x、y、z。后来我慢慢意识到，罪孽深重最大恶极的sin会导致数学变得更加险恶。 为了洞悉数学的险恶，我曾试图将数学以图形图像的方式显示出来，并写过几个程序DEMO可以利用数学公式转化成图形图像。DEMO发在叶飞影 - 博客园里，有兴趣可以去看看。现在很多数学软件都有类似的功能，我只是习惯用自己的这套逻辑，自得其乐而已。文中所发的图片都是从我写的程序DEMO中截屏出来的。 1

正弦波

提到“波”这个词，我第一会想到波波，第二则想到正弦sin。很容易画出函数y=sin(x)的图形：



正弦波

我有个大学同学曾经说过：“人生就像一条正弦波，有时在波峰，有时在波谷。我现在正处于波谷，但我相信将来不久，我就会爬上波峰。” 然而，这个比喻并不准确，否则人生就不会起起落落落落落落落落......了。我觉得更准确的比喻是：人生就像若干条正弦波的叠加，你永远不知道自己下一步是起还是落。



看看这个正弦波叠加函数： y = sin(x) + sin(x*2)/2 + sin(x*4)/4 + sin(x*8)/8 + sin(x*16)/16 + sin(x*32)/32 + sin(x*64)/64 + sin(x*128)/128

有规律的正弦波叠加 该函数由8个正弦波叠加组成，每个波有它的振幅和频率。然而世事无常，每个波的振幅和频率决不会那么地有规律，如果用随机数设置这8个波的振幅和频率，可以得到如下图像：



随机的正弦波叠加 现在问题来了，随意选中图像所绘曲线上的一点，该如何判断该点将来是涨还是跌？涨又能涨多少？跌又能跌多少？这只有知道每个正弦波的振幅和频率才能知道。小时候看电视剧《大时代》，里面讲炒股要追“势”，将股票的波动曲线析构成一个个的“势”的作用结果。通过对股票波动曲线的研究，分析出每个“势”的大小和周期，以此涨势则买入，跌势则卖出，无往不利。

然而单看这么一根根屌丝一样的曲线，我是没有办法得到振幅和频率的具体数值，我甚至连有几个正弦波都看不出来。理论是美好的，现实是残酷的，我断然没有这方面的才能，所以不敢踏入股市。就如同我知道一点点概率论的知识（投入值大于期望值八成会亏本），就不敢买彩票一样。 加大正弦波的振幅，加快正弦波的频率，可以生成类似下面这样的图像：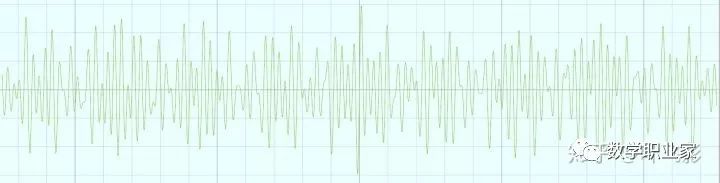



波动图

是不是感觉有点乱糟糟的，还可以更乱吗？当然可以！ 看看函数：y = fract(sin(x)*1000000.0)。fract是对实数忽略整数位只取小数位的操作。这个函数的图像如下：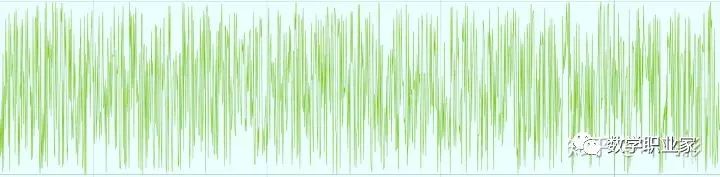



随机图

这个函数的用处就是为了生成随机数。当然真正大神写的随机数生成的函数是： y = fract(sin(x*12.9898)*43758.5453123)。

至于为什么设置12.9898和43758.5453123这两个常数值，我也不知道呀！大神的思维不是我等凡人所能理解的，我只知道如果设置了其他数，生成的数值可能就不够随机了。 2

二维三维......

题目提到的方程是个二元方程，对应的图形是个二维图形。我们先从简单的来讲： 函数y = sin(x)扩展到二维可以是z = sin(x) + sin(y),也可以是z = sin(x + y)，还可以是z = sin(x）*sin(y)、z = sin(x * y)。

每一个函数都是让人头晕目炫，凭我怎么去想，也想不清晰这些函数应该是什么样。

有一天晚上，我半夜醒来睡不觉，就闭着眼睛想z = sin(x) + sin(y)这个函数应该是什么样，这货应该是圆的还是方的呢？怎么都想不清楚，第二天早上，起来用程序画了一下。OK，原来它是这个样子的：



z = sin(x) + sin(y) 加点伪彩颜色后，看让去不会那么让人眼晕：



z = sin(x) + sin(y) 原来这货是既圆又方，这图像真让人眩晕，如果那晚我能想象出这个函数的图像，应该会很快再度安然入睡。。 方程sin(x) + sin(y) = 1的图像：



sin(x) + sin(y) = 1 方程sin(x) + sin(y) = 0的图像：



sin(x) + sin(y) = 0 如果再增加一维，函数变为：w = sin(x) + sin(y) + sin(z)，这就有点难画了。

这是个三维函数，属于体素数据，是个实心的。

要看体素的内部数值，可以使用体绘制，但我只有显示其切片的办法。当然切片不一定是平面，可以用个曲面来切，将切到的数值以颜色的形式显示出来。

下图为用一个半径为40的球体切割函数w = sin(x) + sin(y) + sin(z)，然后把数值转化成灰度，得到的图形：



w = sin(x) + sin(y) + sin(z) 灰度图看着不爽，加点伪彩颜色瞧瞧：



w = sin(x) + sin(y) + sin(z) 球看着也不爽，既然z = sin(x) + sin(y)可以生成一个平面地形高度图形，那么就可以用w = sin(x) + sin(y) + sin(z)生成一个星球高度图形：



w = sin(x) + sin(y) + sin(z)



w = sin(x) + sin(y) + sin(z) 如果你们还想知道四元及以上的可视化效果，诸如：k = sin(x) + sin(y) + sin(z) + sin(w)，我也没办法啊！四维世界的险恶，我做为三维世界的生物根本看不到，也想不懂。 3

sin(x²)+sin(y²)=1

话题回到问题中的方程上。先看函数y = sin(x²)，我们可以很容易画出它的图像：



y = sin(x²) 然后将一元变量的函数扩展到二元变量：z = sin(x²)+sin(y²) 可以将该函数以地形高度图的方式进行显示：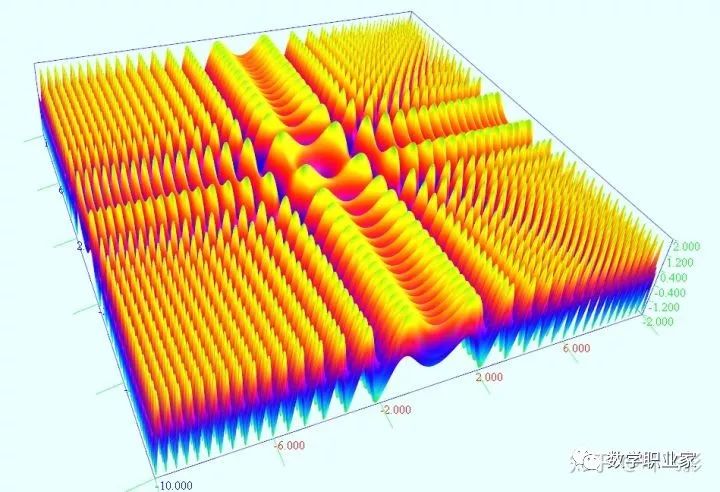



正面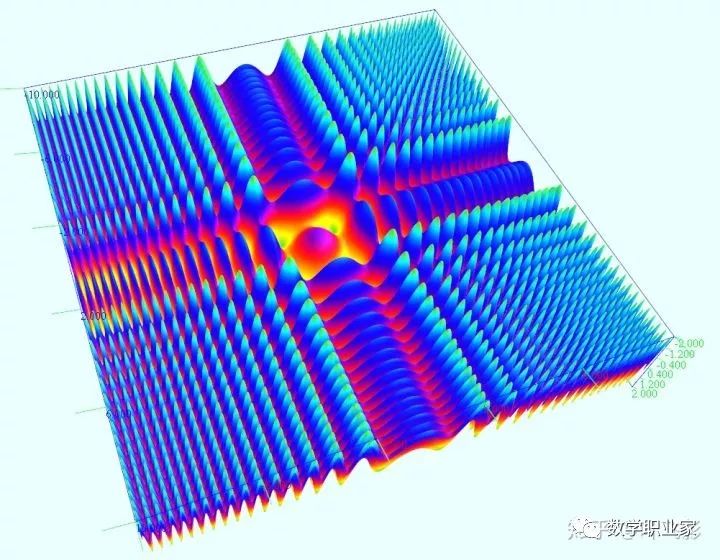



反面

然后用平面z = 1横切该地形，就可以得到方程sin(x²)+sin(y²)=1的图像：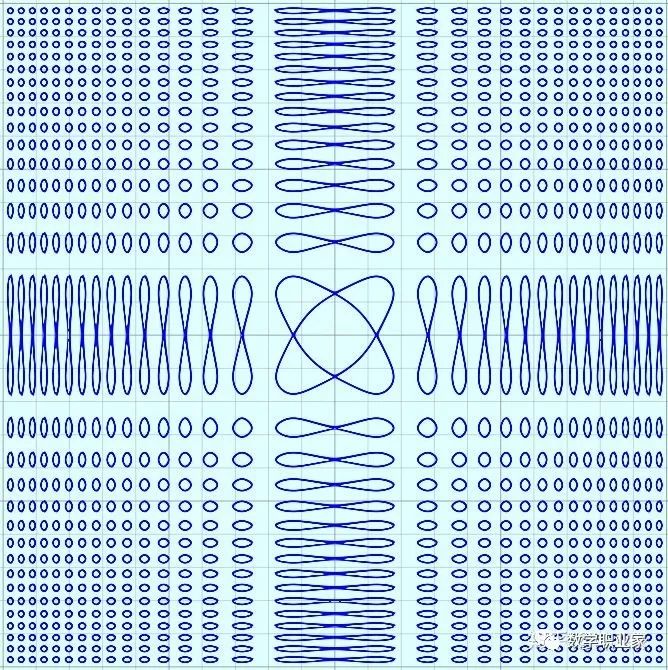



sin(x²)+sin(y²)=1 不过我更愿意将z转化成一个像素值而不是高度值，下图为将z转化成灰度值生成的一幅黑白图像：



灰度图 可以将z = 1的区域用红色标识一下：



灰色图+勾勒sin(x²)+sin(y²)=1 既然是灰度值，就可以对其做伪彩调色，以生成更漂亮的彩色图像：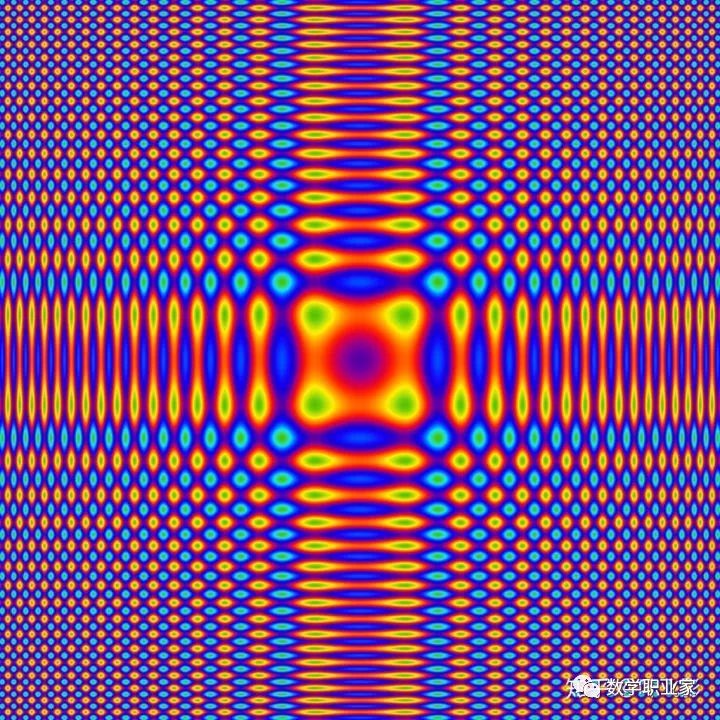



伪彩图1



伪彩图2



伪彩图3

再增加一维，函数变为：w = sin(x²) + sin(y²) + sin(z²)。下图为用一个半径为10的球体切割得到的图形：



w = sin(x²) + sin(y²) + sin(z²)



w = sin(x²) + sin(y²) + sin(z²)



w = sin(x²) + sin(y²) + sin(z²)



w = sin(x²) + sin(y²) + sin(z²) 最后，大家想不想看看方程sin(x²)+sin(y²)+sin(z²)=1的图形效果？图形中含有很多可爱的激凸哟！



数值范围(-2.2, 2.2)



数值范围(-3.3, 3.3)



数值范围(-4.15, 4.15)



数值范围(-10, 10)



数值范围(-10, 10) 当然也有方程sin(x²)+sin(y²)+sin(z²)=0的图形效果，密集恐惧症患者的福利：



数值范围(-6, 6)



数值范围(-10, 10)

审核编辑：刘清