电动汽车的引擎,医学中的磁共振成像,厨房中的电热水壶,你的智能手机的充电器,无线电,WiFi等等。任何利用电或磁的设备基本上都是基于麦克斯韦方程(Maxwell equations)的。
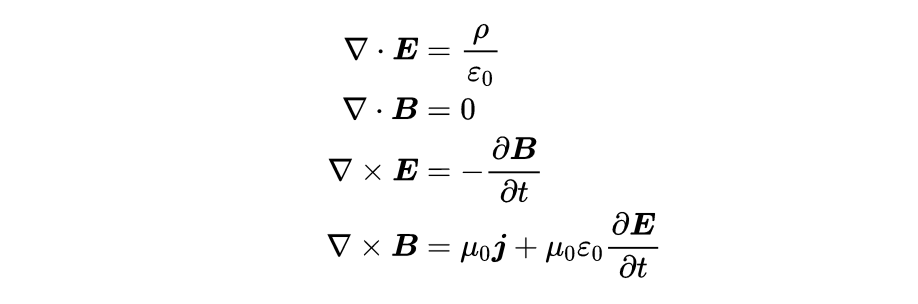
本文的目标不是理论或实验证明麦克斯韦方程,而是尽可能简单易懂地呈现它们。我还会解释麦克斯韦方程中出现的数学概念。然而,首先,你应该知道什么是偏导数以及什么是积分。要理解所有的麦克斯韦方程,你还要知道什么是电场和磁场。
考虑一个带有电荷“Q”的大电荷球和一个带有电荷“q”的小电荷球。这两个球体相距r,它们之间的电力由库仑定律(coulombs law)给出。
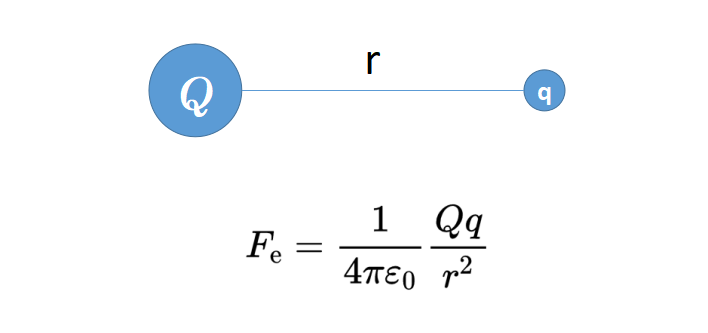
现在,如果你知道大电荷的值,想知道大电荷对小电荷施加的力的值怎么办?但是,你并不知道这个小电荷的具体值,或者你有意将这个值保持开放,只想看大电荷(对其)施加的力。
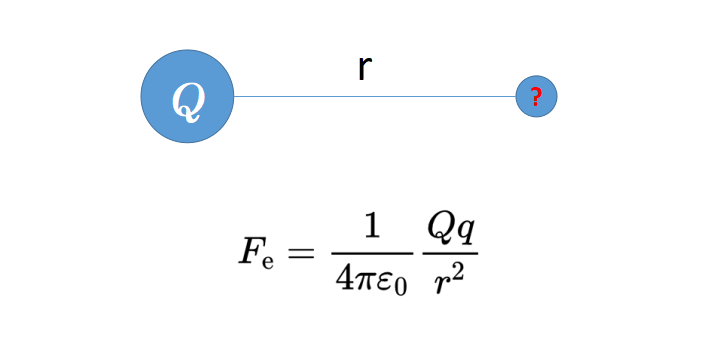
因此,你必须以某种方式从库仑定律中消除小电荷q。为此,你只需在库仑定律的两边都除以q。这样,右边的小电荷就消失了,反而出现在等式的左边。
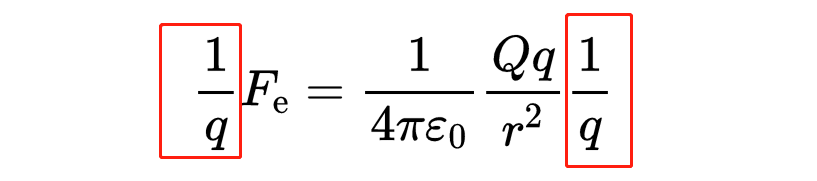
左边“F/q”被定义为源电荷Q的电场E,(称其为源电荷)是因为电荷Q是电场的源头。
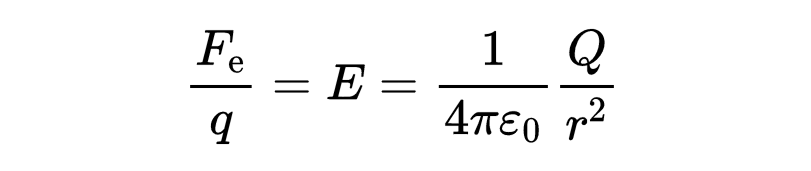
电场E因此表示在与源电荷距离r的位置放置一个小电荷时,会作用于它的电力。到目前为止,只考虑了电场的大小,即电场的强度,而没有考虑电场的精确方向。然而,麦克斯韦方程是通用的,也包括电场的方向。因此,我们必须将电场转化为向量。
向量以粗体显示。手写时,大多数人会在字母上面加一个小箭头,以区别于标量。我省略了箭头。三维空间的电场E作为向量具有三个部分(分量)Ex,Ey和Ez,
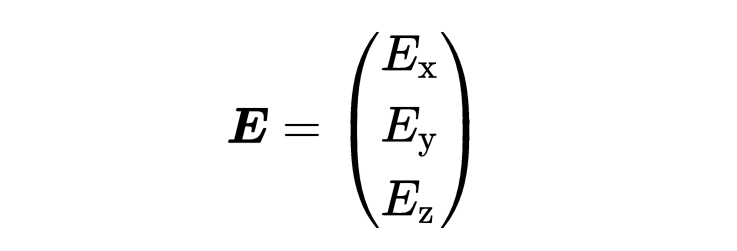
让我们看看第一个部分。第一个部分依赖于空间坐标(x, y, z),是x方向的电场大小。也就是说,根据(x, y, z)的具体位置,Ex的值是不同的。
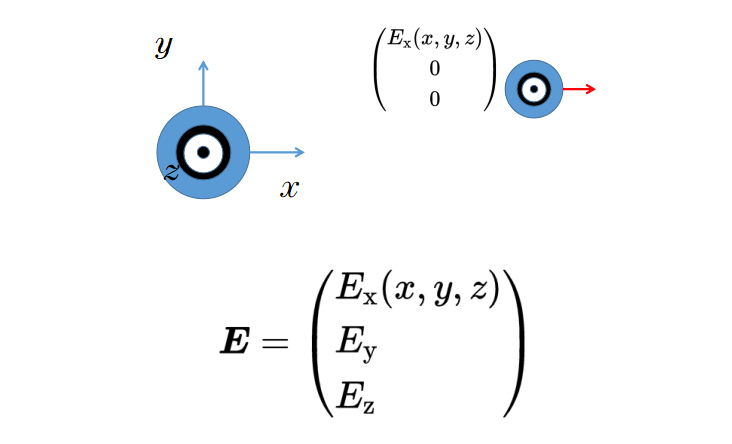
同样的规则也适用于其它两个部分Ey和Ez,它们分别表示y方向和z方向的电场强度。
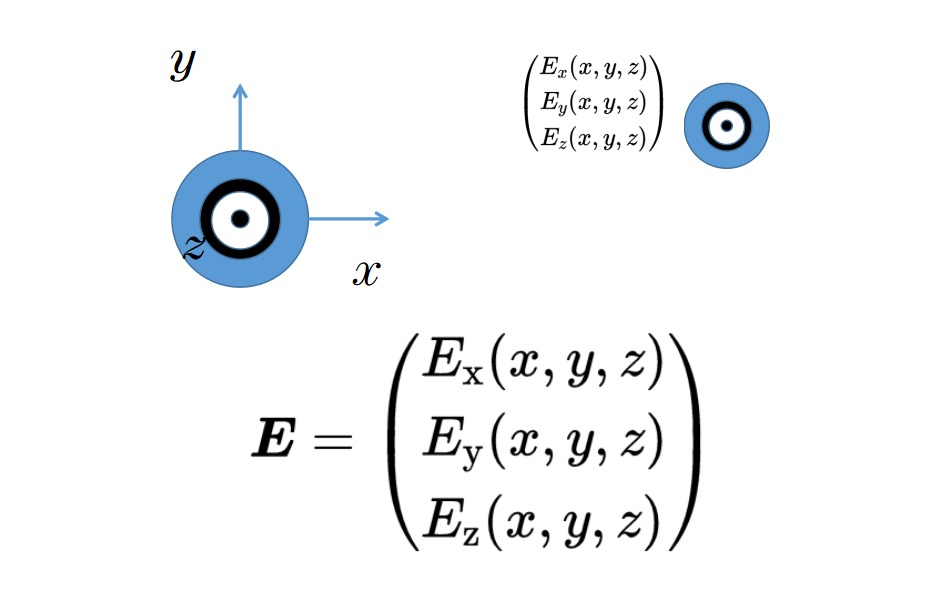
电场的分量表明在特定位置的测试电荷在第一,第二或第三个空间方向上会受到哪种电力作用。
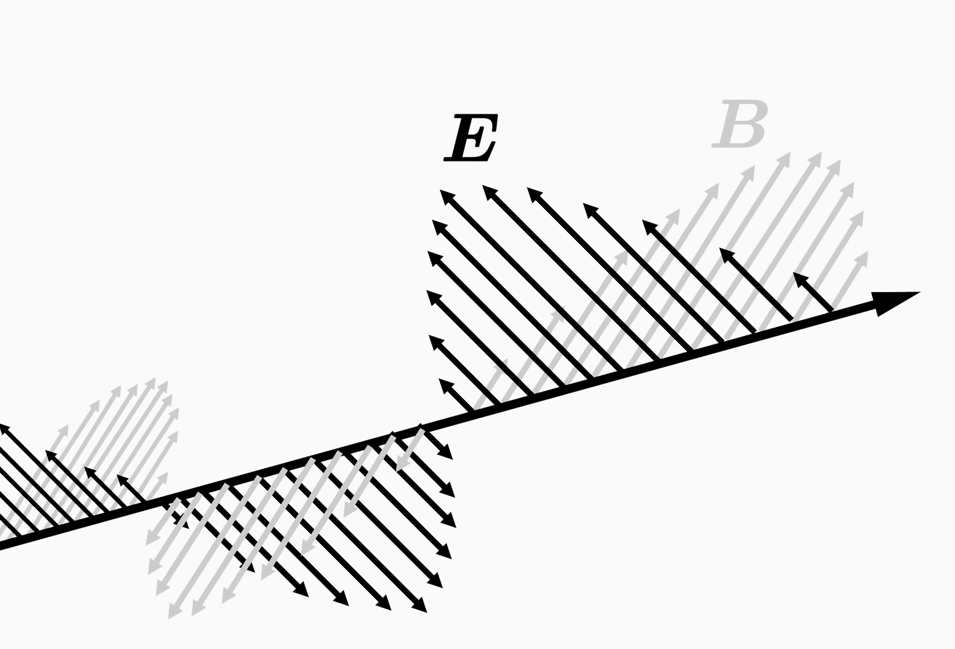
麦克斯韦方程中的另一个重要物理量是磁场B。实验证明,一个带有电荷q的粒子在外部磁场中以速度v移动会受到磁力的作用,这使得粒子偏离原来的路径。粒子上的力与其电荷q和速度v成正比,也就是说,如果电荷或速度加倍,那么作用在粒子上的力也会加倍。
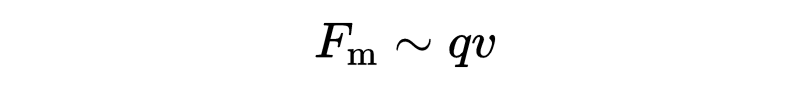
但不仅如此!力也与所施加的磁场成正比。为了描述力和磁场之间的这种比例关系,我们引入了物理量B。这个量的单位必须使得等式右边的单位为力的单位,也就是“牛顿”或“千克米每秒平方”。
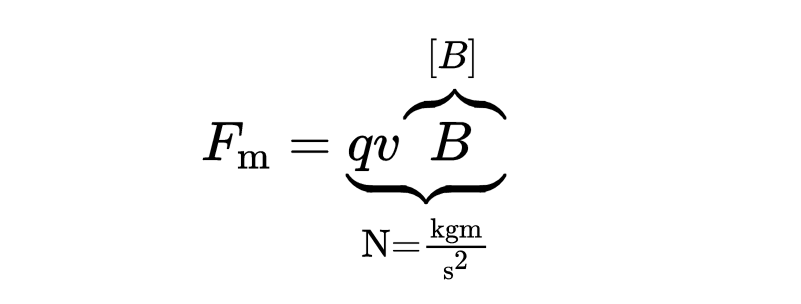
经过简单的转换,你会发现这个单位必须是“千克每安培秒平方”。这就是我们称之为特斯拉(T)的单位。我们把B称为磁通密度(或简称:磁场)。

磁通密度描述了外部磁场,从而决定了作用在带电粒子上的力的大小。公式“qvB”表示带电粒子在磁场中受到的磁力,这仅仅是力的大小。为了像电力一样以向量的形式表达磁力,力、速度和磁场都被表示为向量形式。
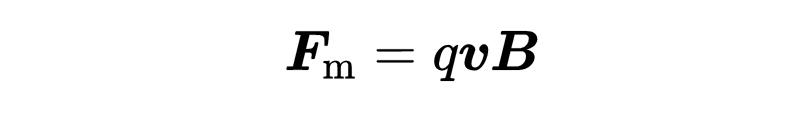
现在,这三个量不再是标量,而是具有x,y和z方向的三维向量。
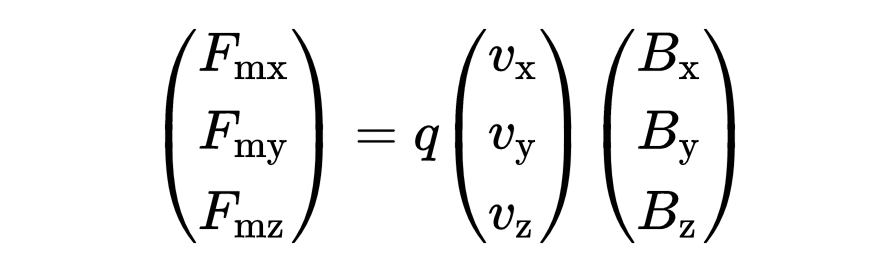
现在的问题是:速度向量v应如何与磁场向量B进行向量乘法?如果你仔细观察磁场中电荷的偏转,你会注意到磁力始终指向与速度和磁场线垂直的方向。这种正交性可以用所谓的叉积来运算。
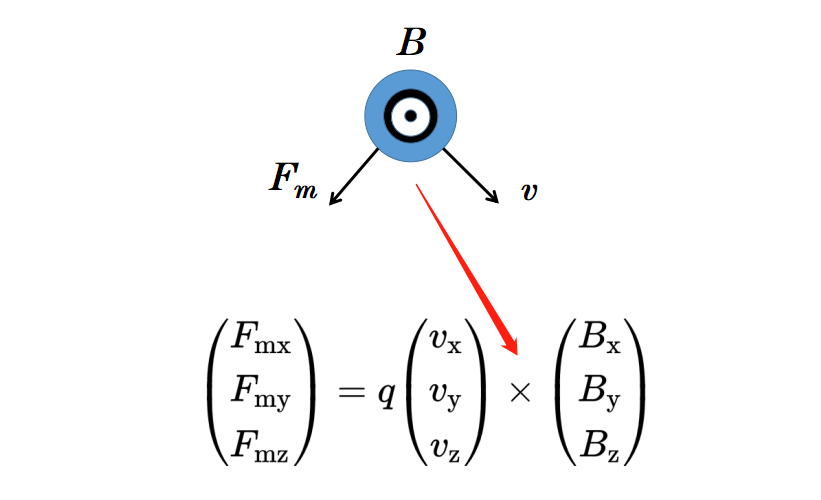
两个向量v和B的叉积是一个向量,总是垂直于向量v和B。
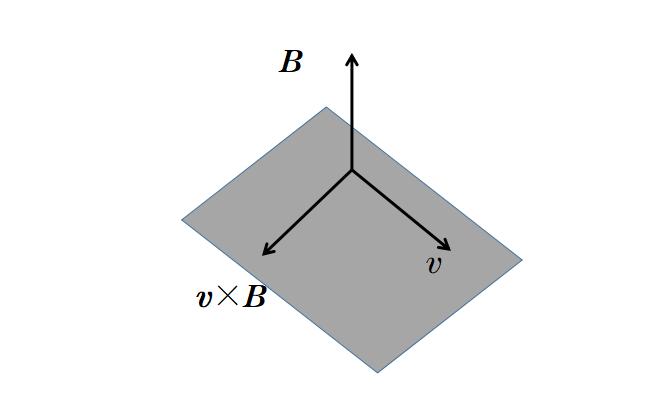
第一个分量是
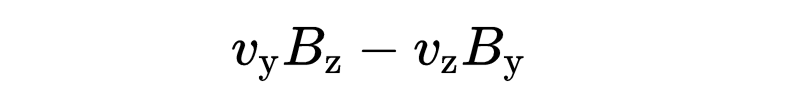
第二个分量是
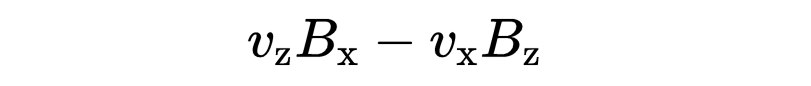
叉积的第三个分量是
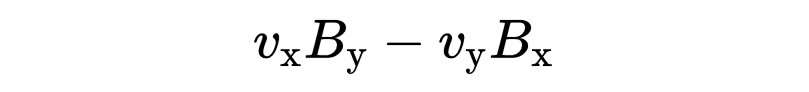
所以
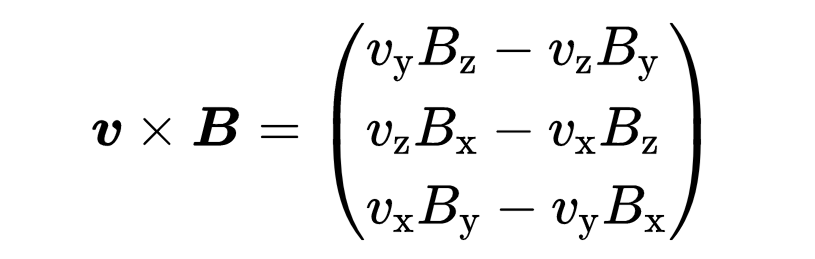
为了使力总是垂直于v和B,我们在公式中取v和B的叉积。所以磁力的向量形式一般为:
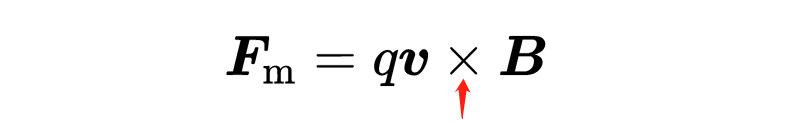
电荷q是一个普通的标量因子。正如你所看到的,物理量B描述了磁场的强度,这会导致移动的电荷发生偏转。
现在你已经学习了麦克斯韦方程中的两个重要物理量,即电场E和磁场B。
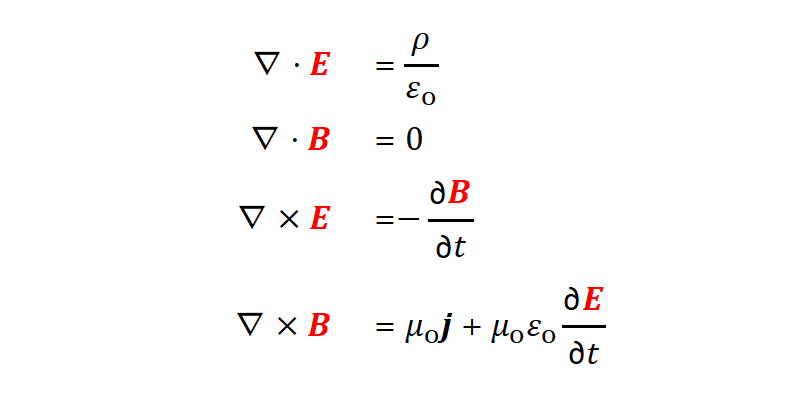
它们都是所谓的向量场。这意味着你可以将一个电场和磁场向量分别赋给空间中的每个位置(x, y, z),这两个向量同时表示了电场和磁场的大小和方向。
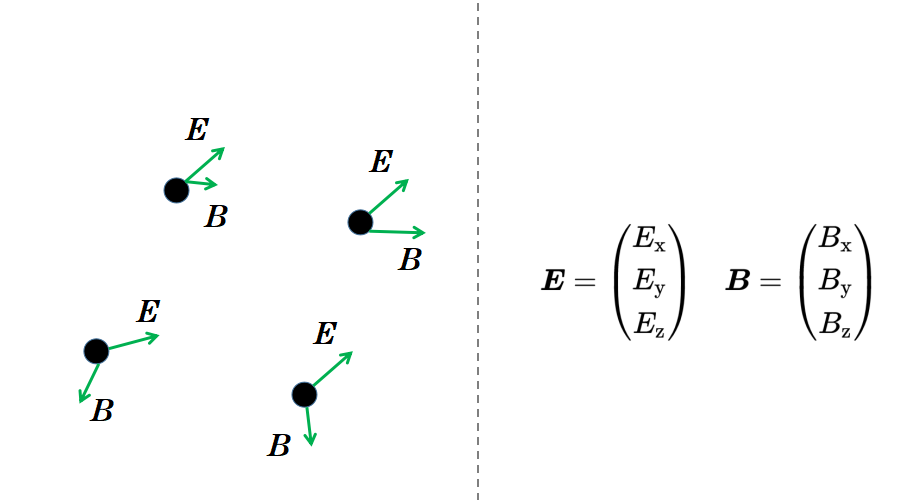
总共有四个麦克斯韦方程。这四个麦克斯韦方程可以用两种不同的方式来表示。有所谓的积分形式,它用积分来表示麦克斯韦方程,
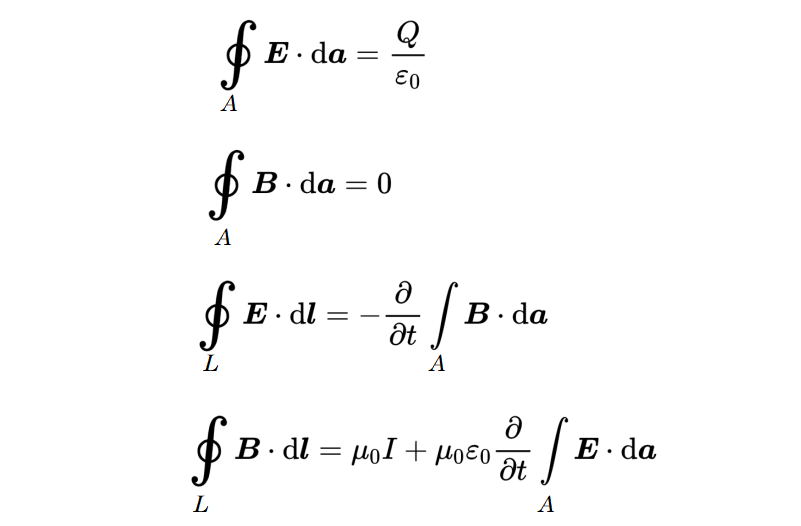
还有微分形式,它用导数来表示麦克斯韦方程:
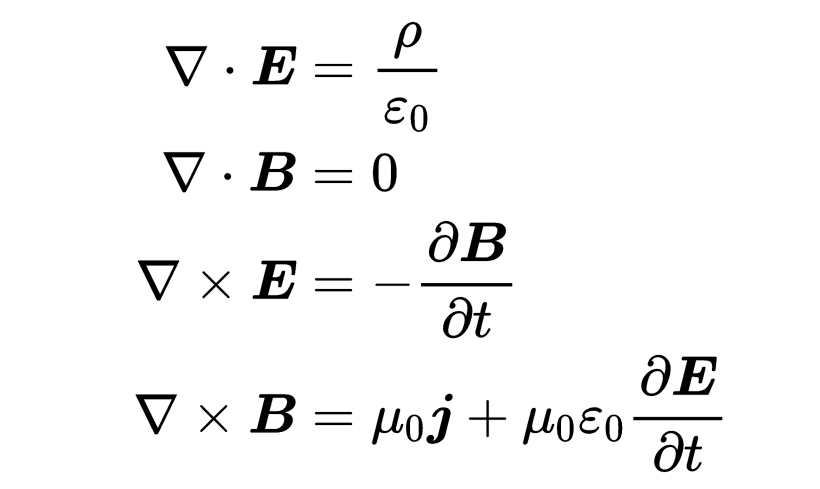
微分形式的麦克斯韦方程对于在空间的一个单点计算磁场和电场是有用的,而积分形式则用于在整个空间区域内计算场。
积分形式适用于计算对称问题,例如计算带电球体、带电柱体或带电平面的电场。
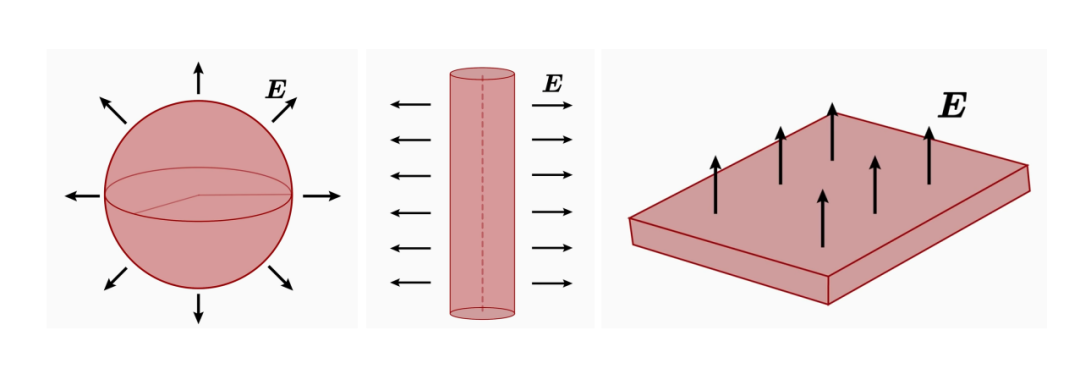
微分形式更适用于用计算机计算复杂的数值问题,或者例如,用于推导电磁波。
另外,微分形式看起来比积分形式更紧凑。两种形式都很有用,可以通过两个数学定理相互转化。一个定理被称为散度积分定理(Divergence integral theorem),另一个是旋度积分定理(curl integral theorem)。如果你理解了这两个定理,那么你就会更容易理解麦克斯韦方程。让我们先来看看散度积分定理。
散度定理
这是散度积分定理的完全形态:
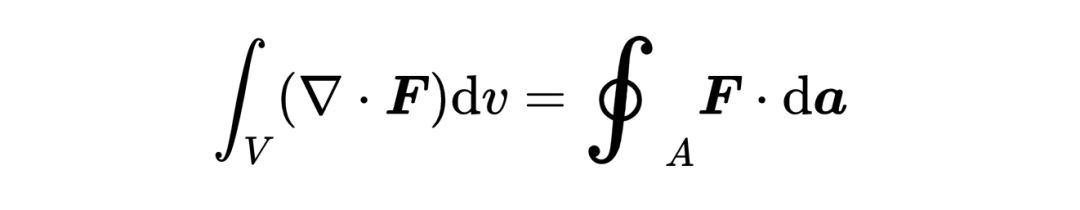
首先,让我们看一下等式的右边,
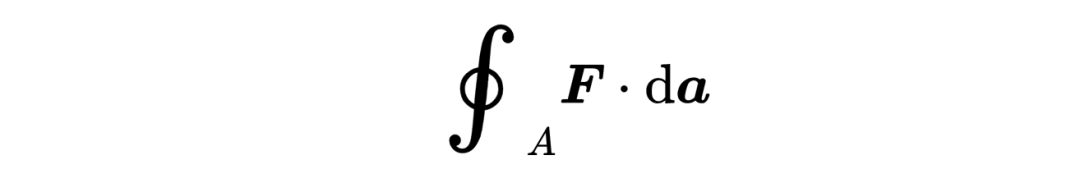
这里的A代表一个封闭任何体积的表面,例如立方体、球体或者你能想到的任何三维物体的表面。

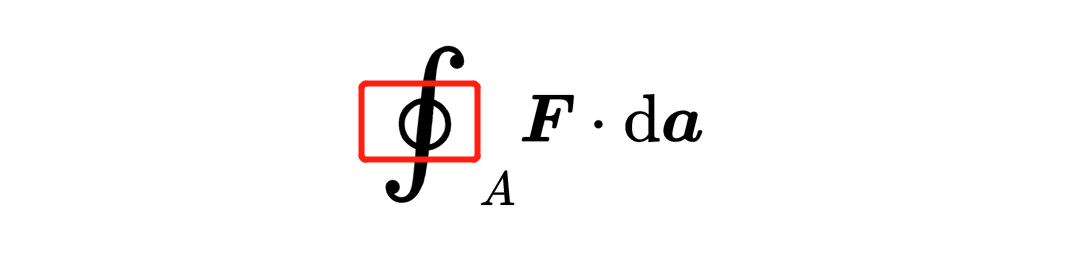
在积分符号上的小圆圈表明这个表面必须满足一个条件:表面必须是封闭的,也就是说,它不能包含任何的孔洞,以便在数学上保证这个条件。因此,表面a就是一个封闭的表面。
这里的F是一个矢量场,可以表示电场
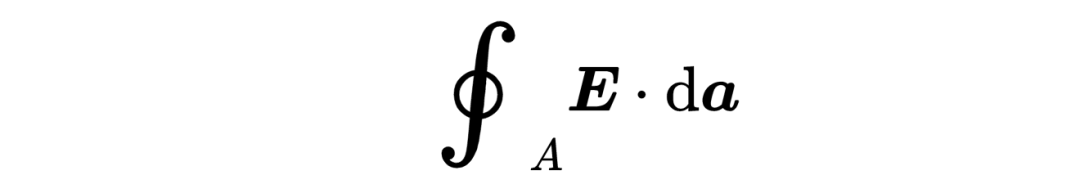
或磁场,
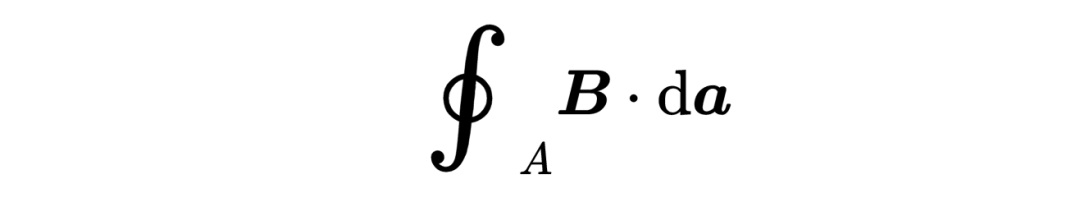
当我们在考虑麦克斯韦方程的时候,它是一个有三个组成部分的矢量,
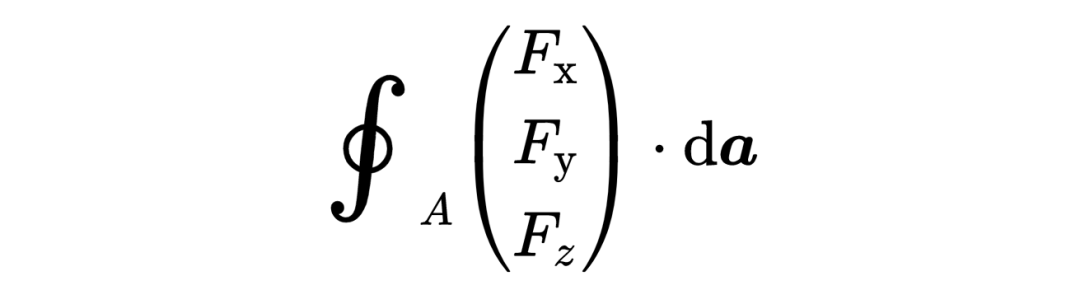
da是无穷小的表面元素,就是所考虑的表面A的无穷小表面元素。
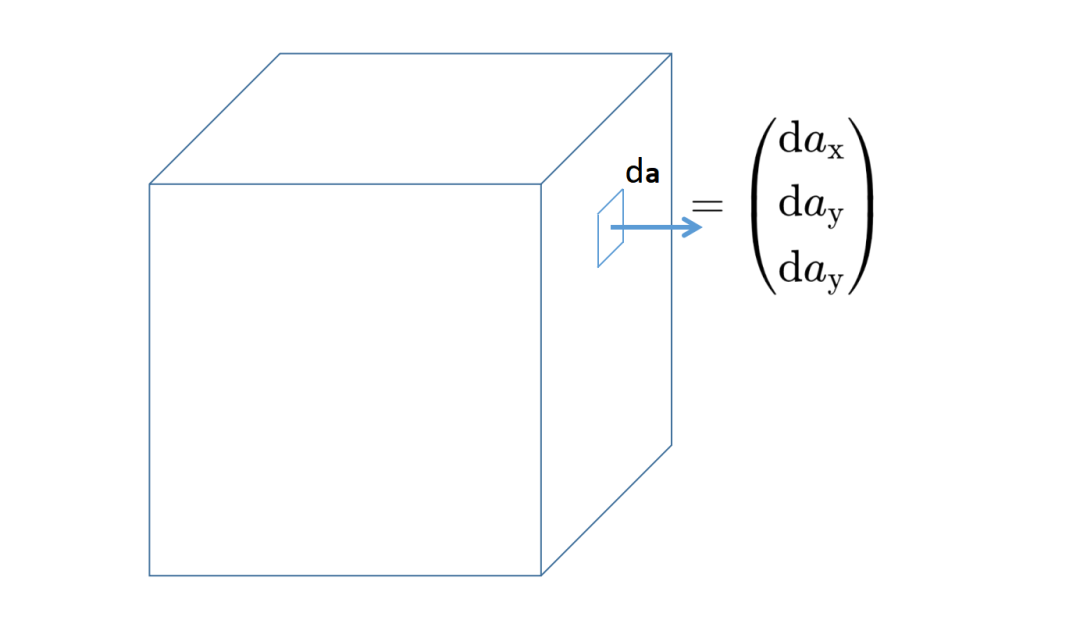
你可能已经注意到,da元素中的a是加粗的,所以它是一个有大小和方向的矢量。da元素垂直于表面,并且定义为从表面指向外部。

在矢量场和da元素之间的点代表所谓的标量积。标量积是一种乘两个矢量的方法,所以在这里,矢量场和da元素之间的标量积是形成的。标量积的定义如下:
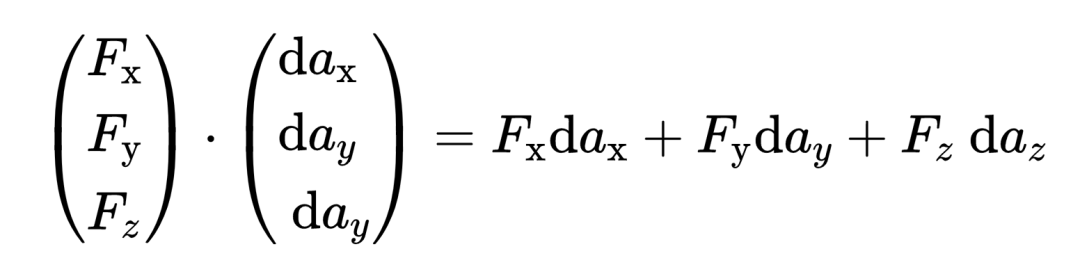
从定义中可以看出,两个矢量的第一,第二和第三组成部分是相乘然后相加的。标量积的结果不再是一个矢量,而是一个普通的数字。
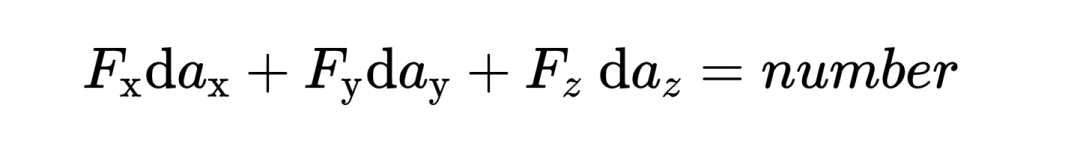
为了理解这个数字的含义,你首先要知道任何矢量都可以写成两个其他矢量的和,
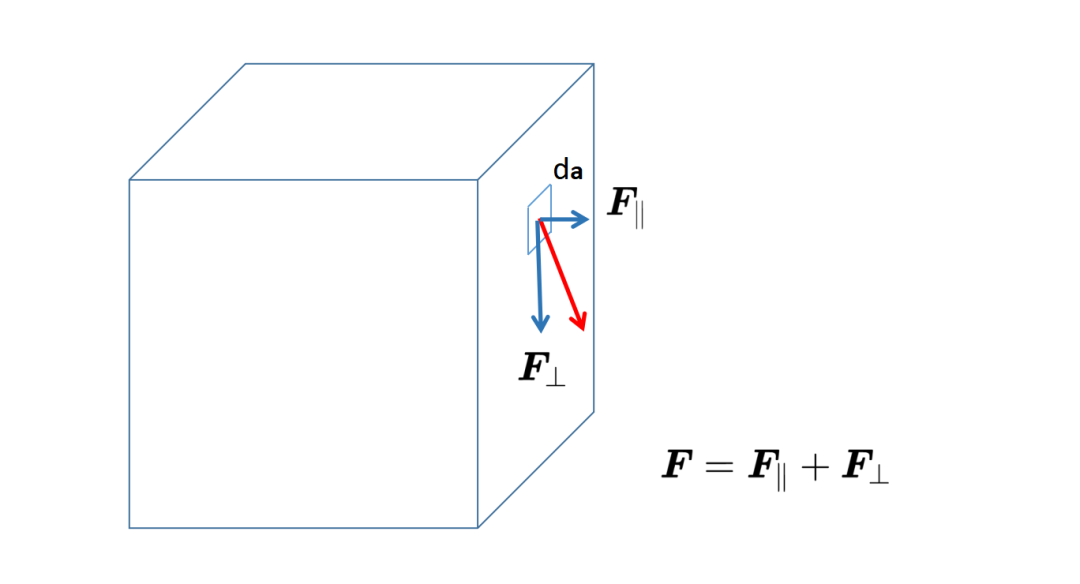
其中一个矢量平行于da元素,我们称之为F平行,另一个矢量垂直于da元素,我们称之为F垂直。另一个数学事实是,两个垂直矢量的标量积总是等于零,这就意味着,
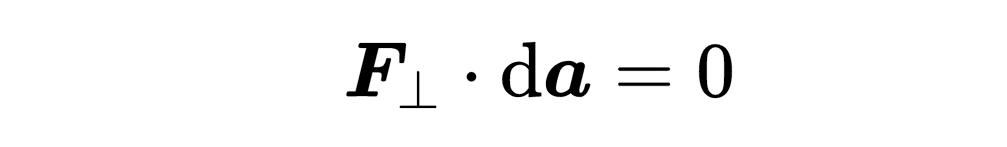
然而,F平行和da元素之间的标量积通常不是零,
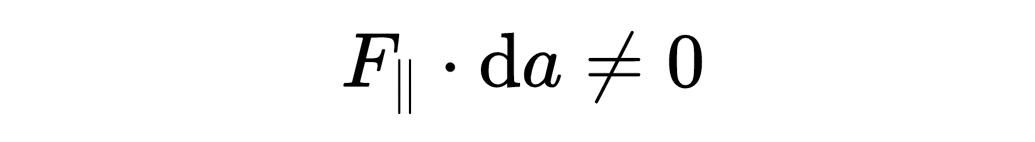
所以现在你可以看到等式右边的标量积是怎么计算的,
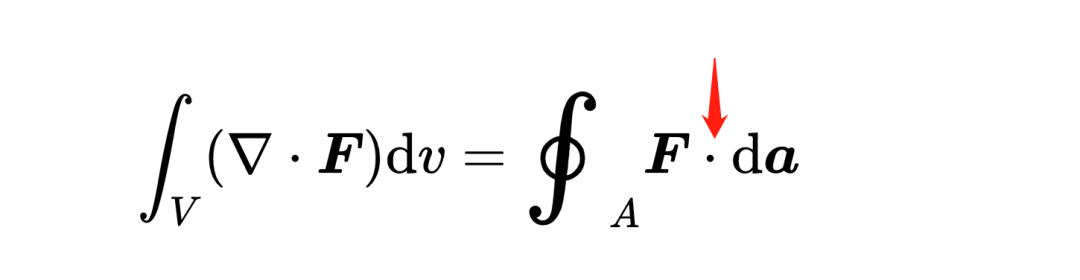
它只选择了矢量场中和da元素平行的部分,剩下的在垂直方向上的矢量场部分被标量积消除。
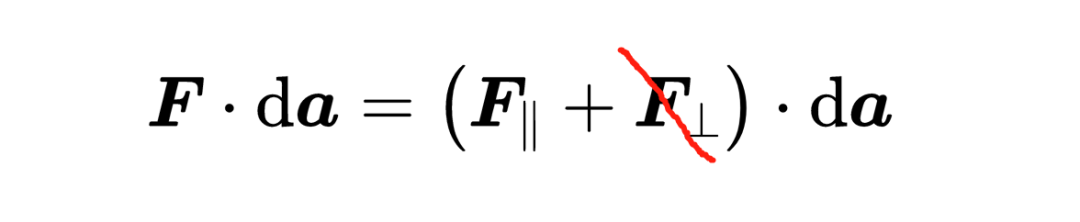
接下来,对于被考虑的表面A的所有位置,都会累加标量积,这就是积分的任务,
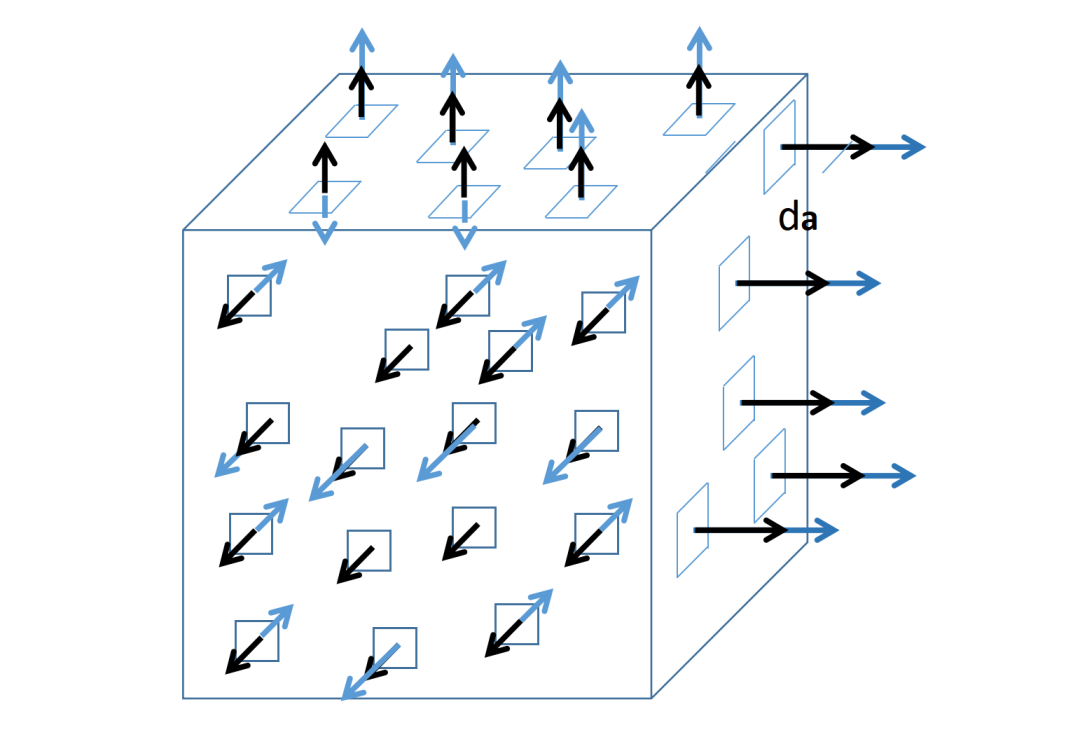
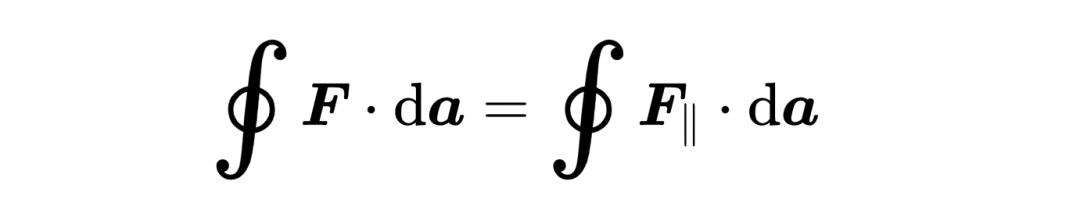
因此,散度定理的右侧会求和所有流入或流出表面A的矢量场F的分量。这种对表面的小片段进行求和的积分被称为表面积分(surface integral)。如果积分函数是一个矢量场,这个表面积分被称为矢量场F通过表面A的流量ϕ。
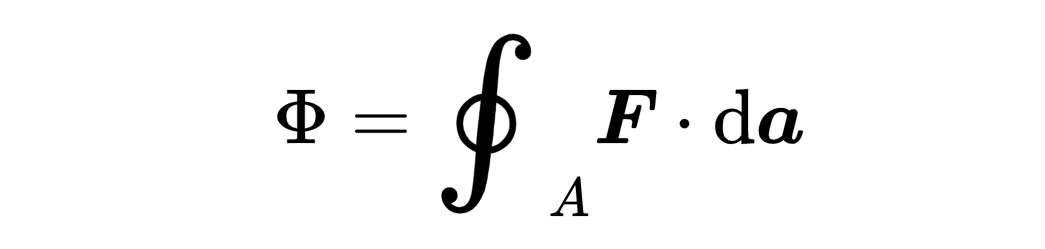
这个描述基于这个表面积分的意义,它度量了多少的矢量场F流出或流入被考虑的表面A。
如果这个表面积分的矢量场F是电场E,那么这个表面积分就被称为通过表面A的电通量。如果矢量场F是磁场B,那么这个表面积分就被称为通过表面A的磁通量。
现在让我们看看定理的左侧,
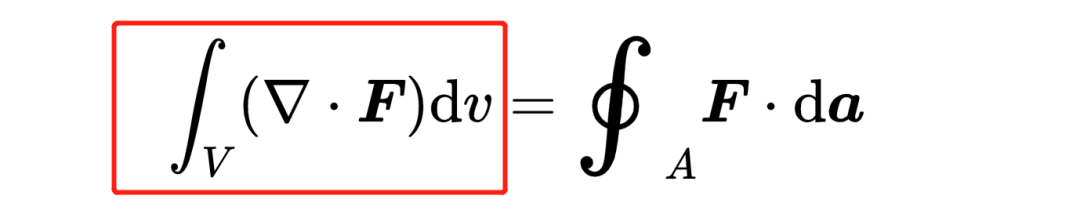
V是一个体积,它是由表面A封闭的体积。dv是一个无穷小的体积元素,换句话说,它是被考虑的体积V的无穷小的体积片段。
上下三角符号被称为nabla算子,它有三个组成部分,就像矢量一样,
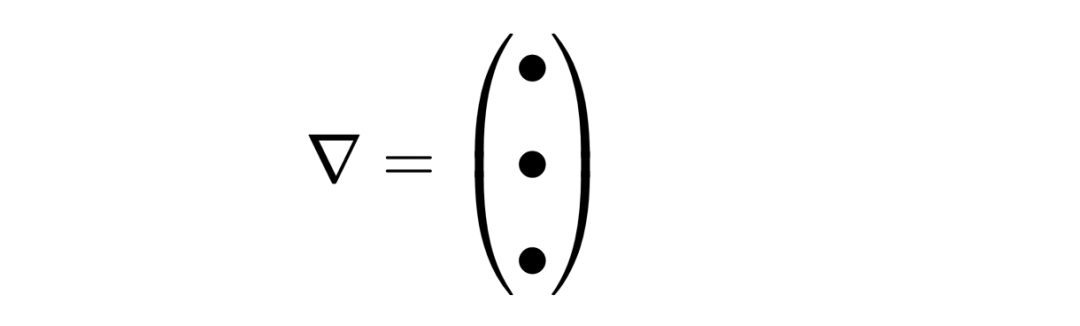
然而,它的组成部分不是数字,而是导数,对应于空间坐标。第一个组成部分是关于x的导数,第二个组成部分是关于y的导数,第三个组成部分是关于z的导数。
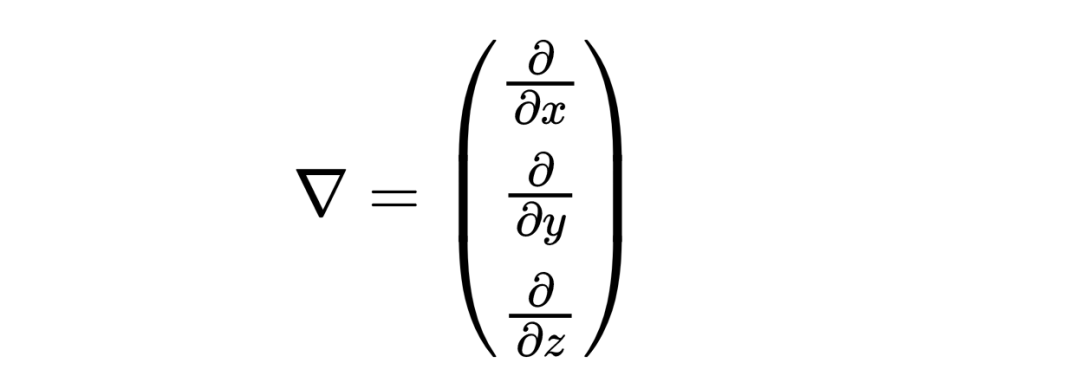
像nabla算子这样的算子只在应用到一个场时起作用,
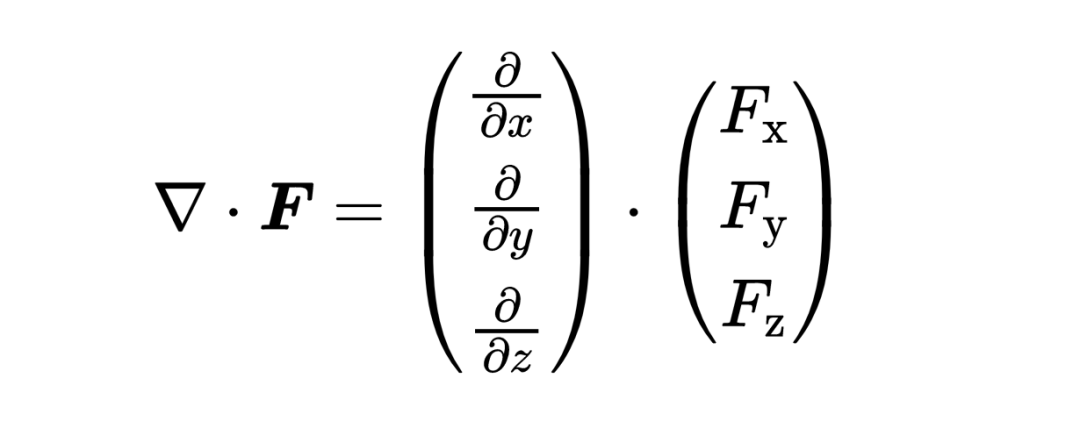
nabla算子应用到矢量场,通过在nabla算子和矢量场之间取标量积。你可以看到,这是矢量场对空间坐标x, y, z的导数的和,
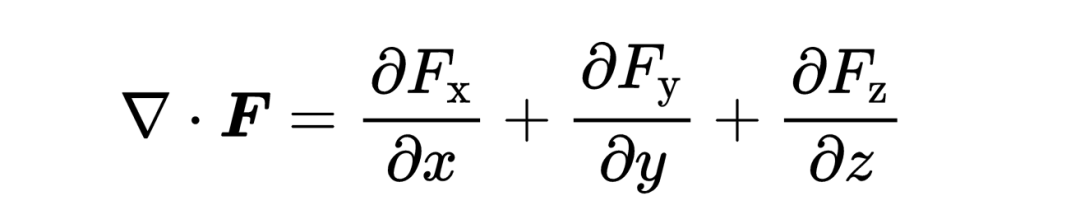
这样一个nabla算子和矢量场F之间的标量积被称为矢量场F的散度(Divergence ofF)。在位置x, y, z的结果不再是一个矢量,而是一个标量,它可以是正的,负的,或者是零。
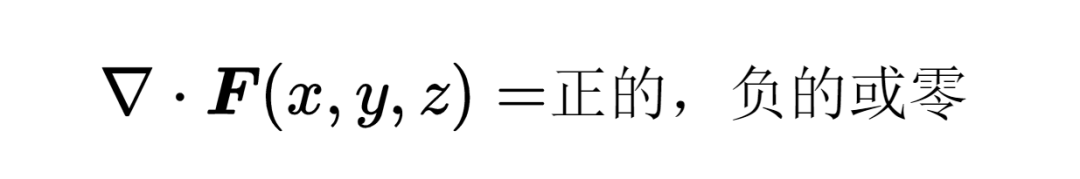
如果在位置x, y, z的散度是正的,那么在这个位置(下图正方体中的圆点)有一个矢量场F的源。如果这个位置被表面包围,那么通过表面的通量也是正的,矢量场可以说是从表面流出。
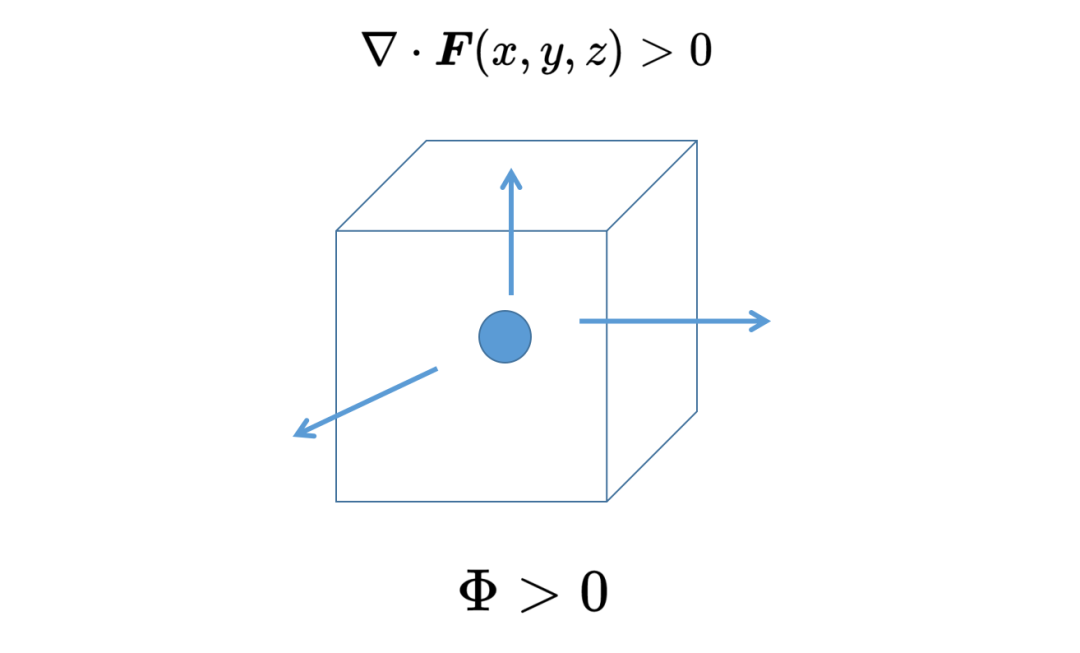
如果在位置x, y, z的散度是负的,那么在这个位置(下图正方体中的圆点)有一个矢量场F的汇,如果这个位置被表面包围,那么通过表面的通量也是负的,矢量场流入表面。
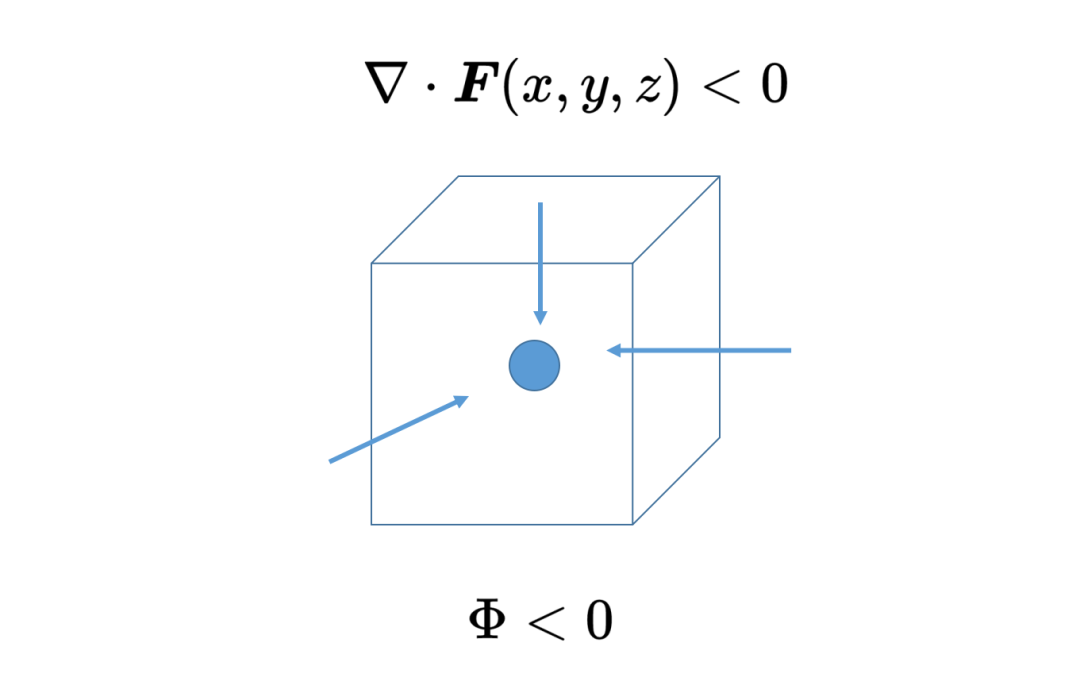
如果在位置x, y, z的散度消失,那么这个位置既不是矢量场的汇也不是源。矢量场不会流出或流入,或者说流入的和流出的数量相等,所以这两个量抵消了。
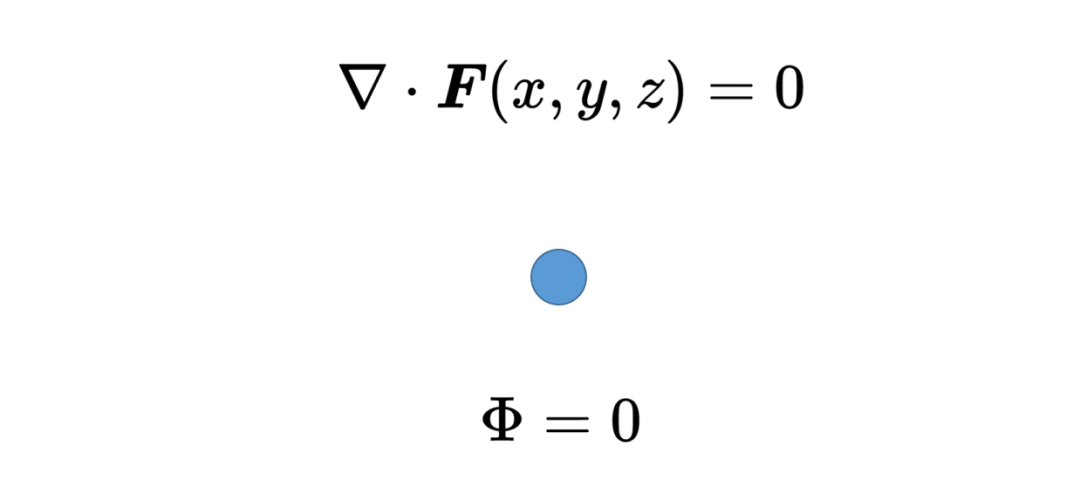
接下来,利用积分在体积内的每一个位置求和散度,即矢量场的源和汇。这种对体积小片段求和的积分被称为体积积分。
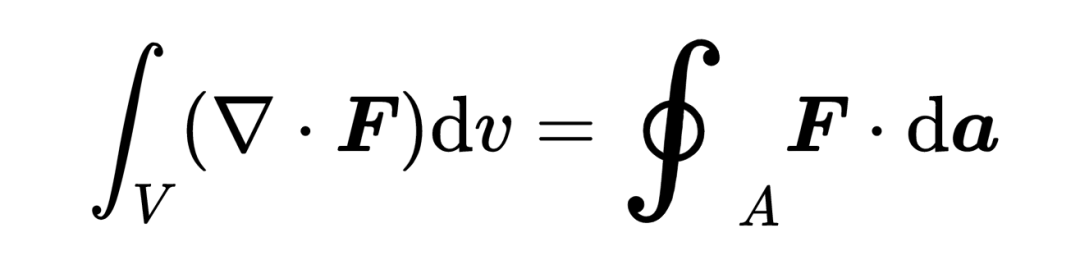
那么让我们总结一下散度定理:在左边是矢量场在体积内的源和汇的总和,而在右边是矢量场通过那个体积的表面的总通量,这两边应该是相等的。散度定理因此表明,在一个体积内的矢量场的源和汇的总和,就是矢量场通过那个体积的表面的通量。
旋度定理
现在考虑理解麦克斯韦方程必要的第二个重要定理,旋度定理(斯托克斯定理),旋度积分定理:
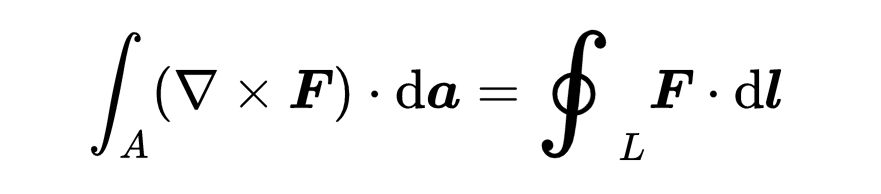
如果你理解了散度积分定理,那么旋度积分定理对你来说不应该很难。你已经知道矢量场F、标量积、Nabla运算符和da元素。首先,让我们看看等式的右侧。
L是空间中的一条线。积分符号上的圆圈表示这条线必须是闭合的,也就是说它应该形成一个循环。

dl是循环的一个无穷小线元素,所以是线的一个无限小的部分。再次,你应该注意到dl元素被显示为粗体,它是一个具有大小和方向的矢量。现在形成了矢量场F和线元素dl的标量积。你已经知道标量积的任务是什么。首先,将矢量场分解为两个部分;一个是平行于dl元素的'F平行',另一个是垂直于dl元素的'F垂直'。
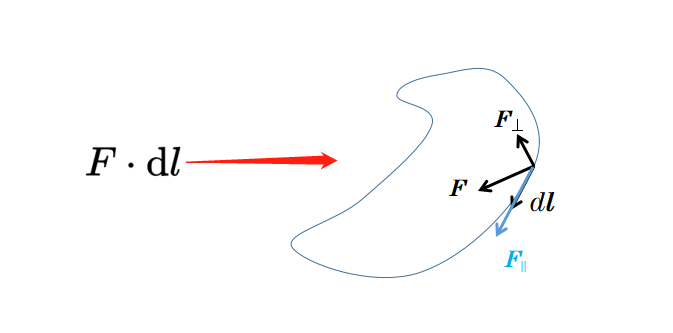
与dl元素的标量积消除了垂直分量,而没有改变平行于dl元素的矢量场部分。因为在每个位置,dl元素都沿着线,所以在标量积中,只有沿着线L的矢量场部分被考虑;矢量场的其他部分被忽略。然后,使用积分对循环的每个位置的标量积进行求和。这样的积分,其中无限小的线元素被求和,被称为线积分。
现在你知道在旋度积分定理的右侧的含义:线积分计算了多少的矢量场F沿着线L运动。
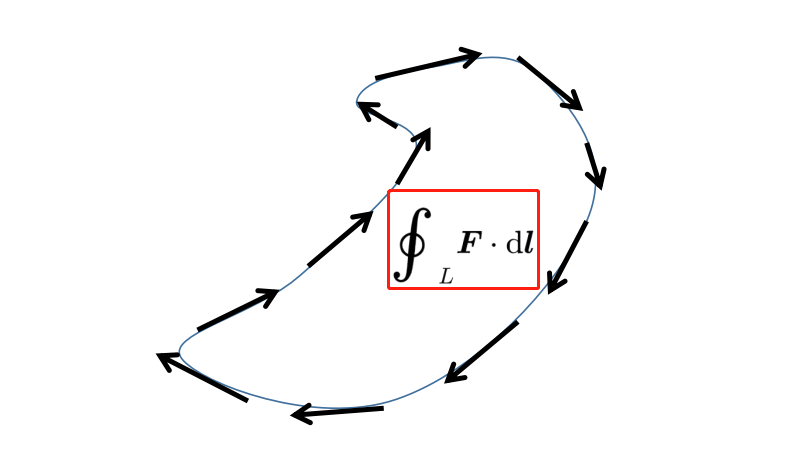
因为线是闭合的,这个标量积返回到求和开始的同一个点。闭合线积分因此表示矢量场F沿着环路L旋转的程度。如果这个线积分中的矢量场F是一个电场E,那么这个线积分被称为线路L上的电压。
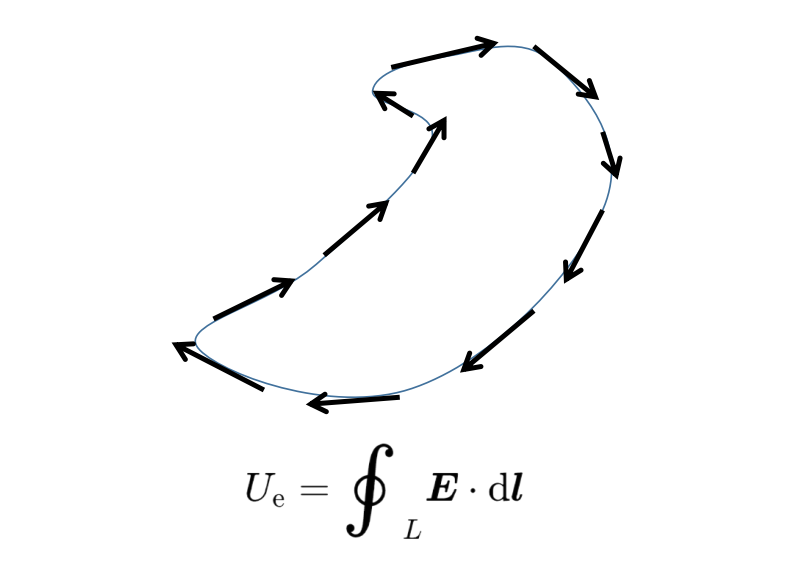
另一方面,当矢量场F是一个磁场B时,线积分被称为线路L上的磁电压。
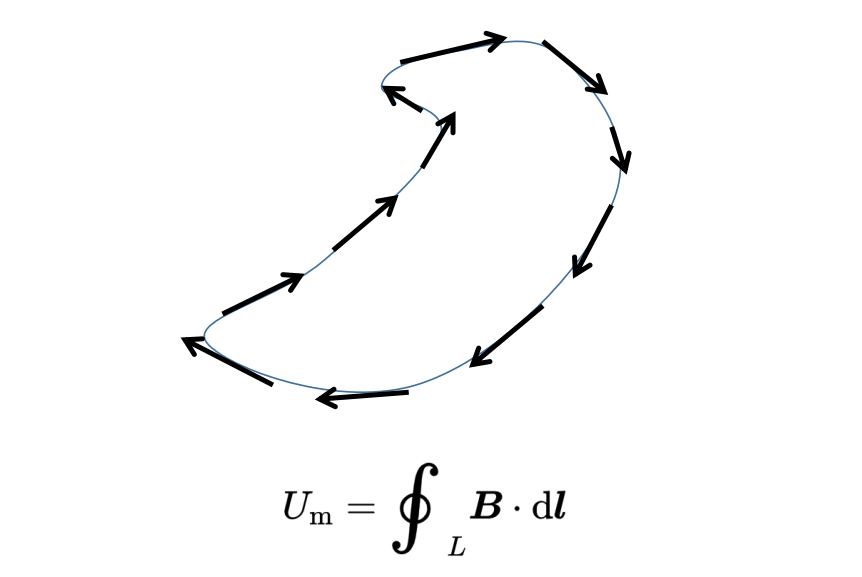
在电场的情况下,电压与通过线路L的正电荷粒子获得的能量成正比。
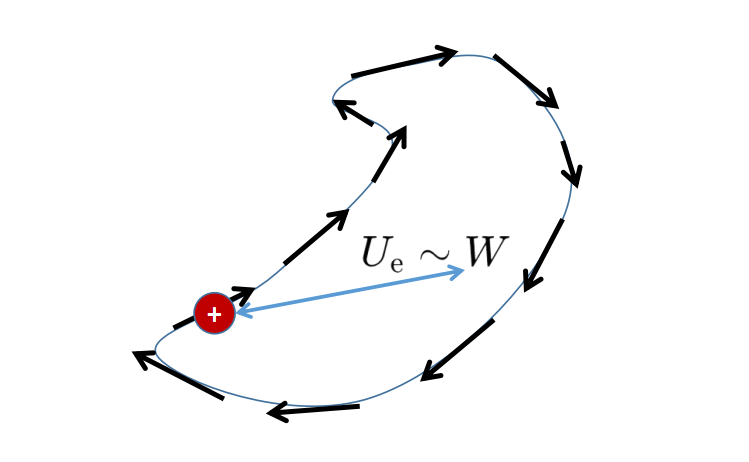
相反,负电荷粒子在通过线路L时会失去这种能量。电场的线积分,也就是电压,衡量了在考虑的线路L通过下,带电粒子的能量增益或能量损失。现在你应该已经理解了旋度积分定理的右侧了。
让我们现在看看左侧。
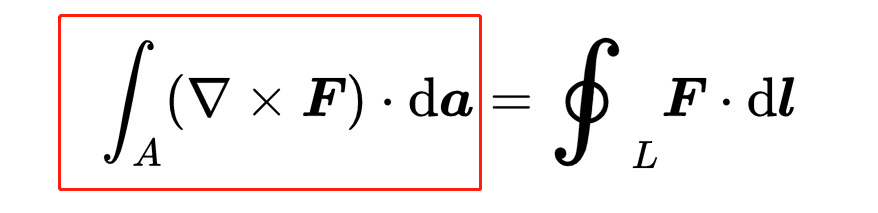
这里再次出现了面积A。这个面,不像散度积分定理,不必是一个封闭的面,而只是线L所包围的面。da再次是面积A的一个无穷小部分,它在任何位置都垂直于该表面。
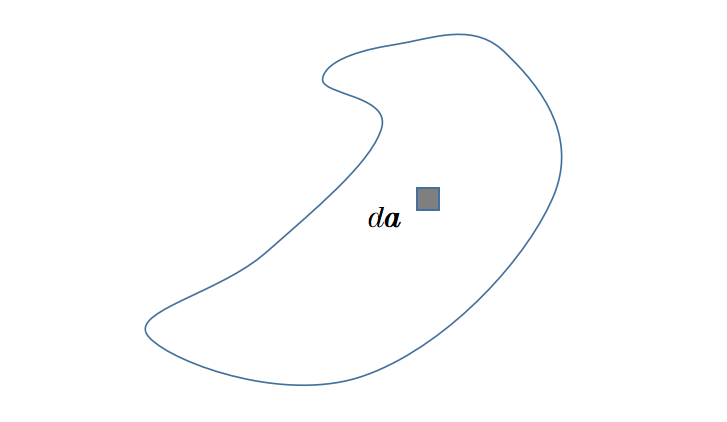
此外,这里出现了叉积,我们在讨论磁力时已经遇到过它。这里,叉积是在Nabla运算符和矢量场F之间形成的。除了标量积,它是两个矢量相乘的第二种方式。Nabla运算符和矢量场F之间的这个叉积被称为矢量场F的旋度。
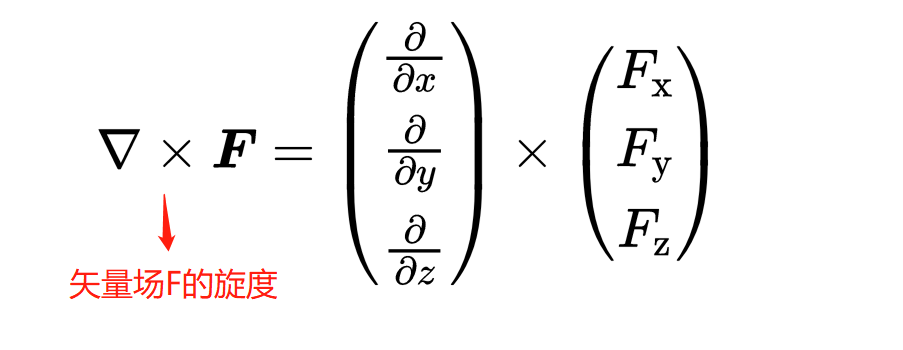
结果(与标量积相反)又是一个矢量场。
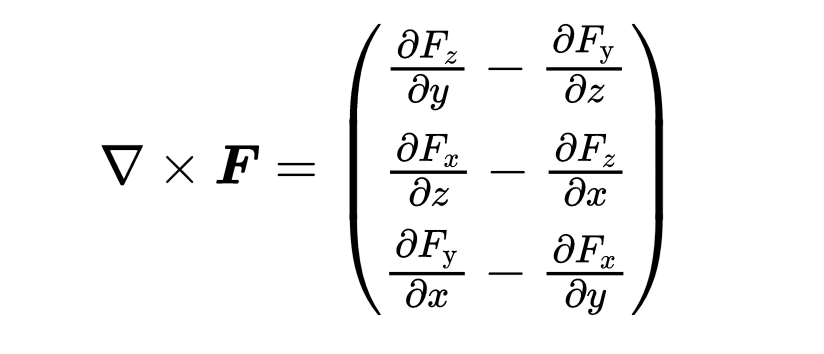
这个新的矢量说明了在表面A内一个点周围,F场有多少旋转。
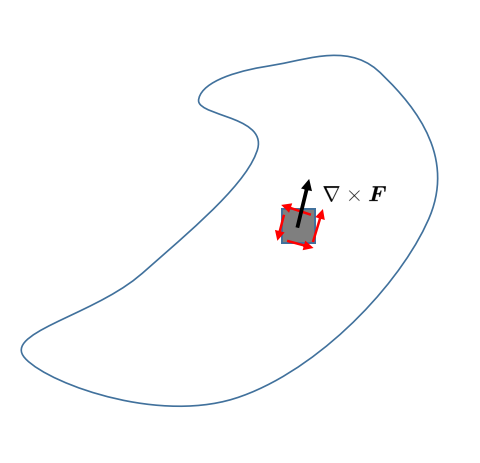
然后,新的矢量场'Nabla叉F'与无穷小表面元素da之间形成了标量积。因此,正如你已经知道的,只有'Nabla叉F'的一部分被留下,这部分平行于表面元素。
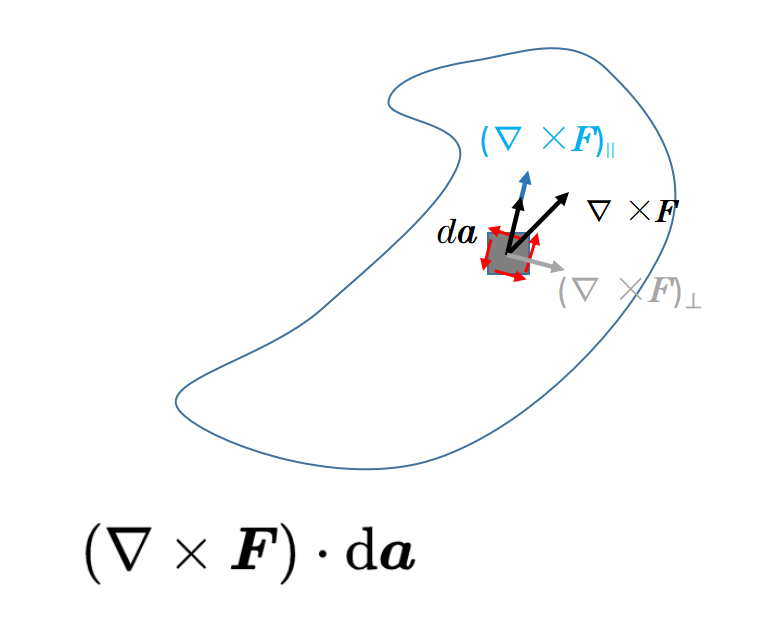
由于表面元素da垂直于表面A,标量积只保留矢量场'Nabla叉F'的一部分,这部分也是垂直于表面A。然后,通过积分,将表面A内的所有标量积分求和。
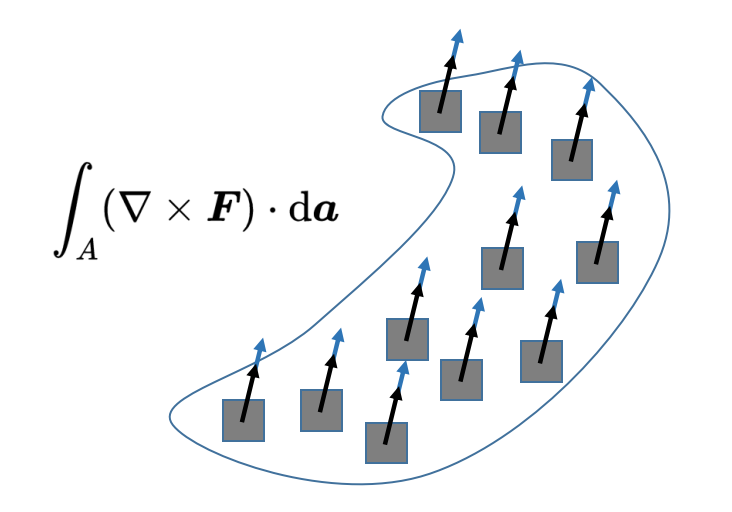
让我们总结一下旋度积分定理的陈述:在右侧,沿着一条线L加总矢量场F,因此,考虑了矢量场围绕封闭表面的旋转。在左侧,对矢量场F的旋度在表面内的每一个独立的点进行求和。根据这个定理,两边应该是相等的。旋度积分定理因此表明,矢量场F在表面A内的总旋度对应于矢量场F沿着该表面的边缘L的旋转。
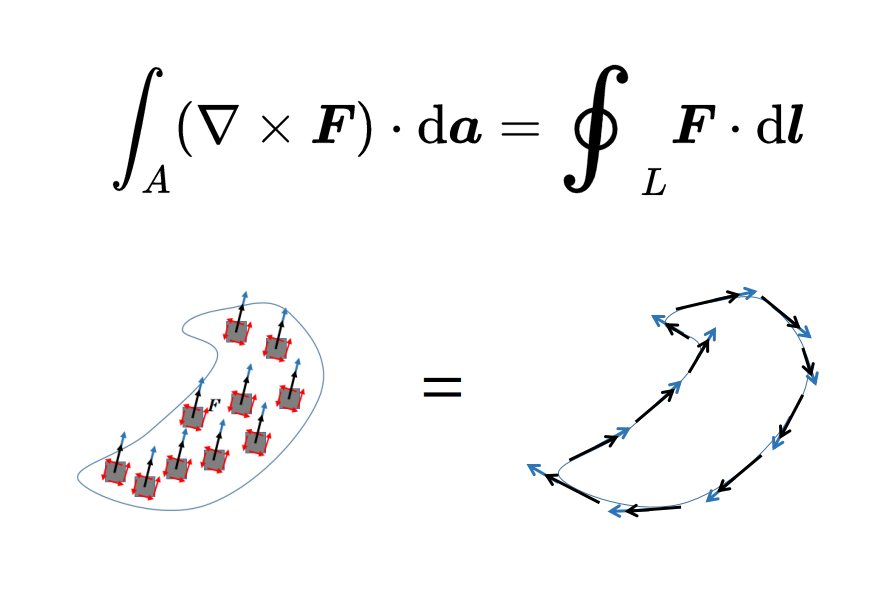
显然,表面内部的矢量场的旋转在求和过程中抵消了,只剩下沿着边缘L的矢量场的旋转。
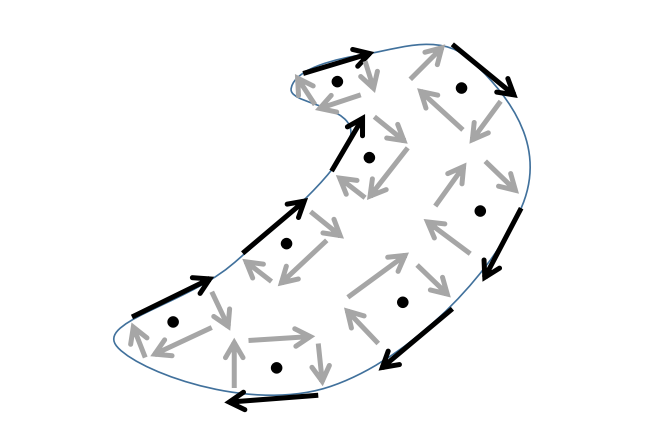
有了所有这些,你现在应该已经准备好完全理解麦克斯韦方程了。
第一个麦克斯韦方程
这就是积分形式的第一个麦克斯韦方程,
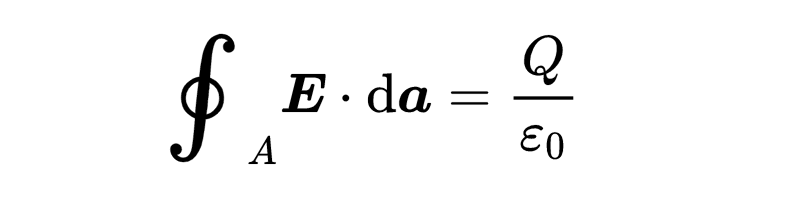
麦克斯韦方程的左侧应该对你来说是熟悉的。这是一个表面积分,其中出现了电场E。这个积分计算有多少电场出入表面A。
因此,这个积分代表了通过表面A的电通量。
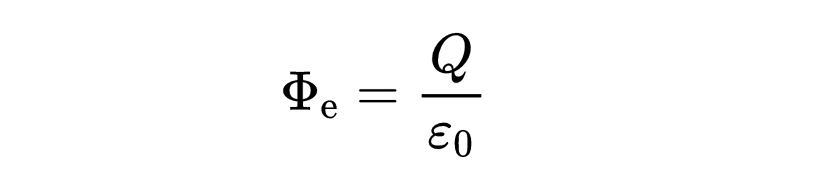
右侧是被表面A包围的总电荷Q,除以电场常数(以得到正确的单位)。
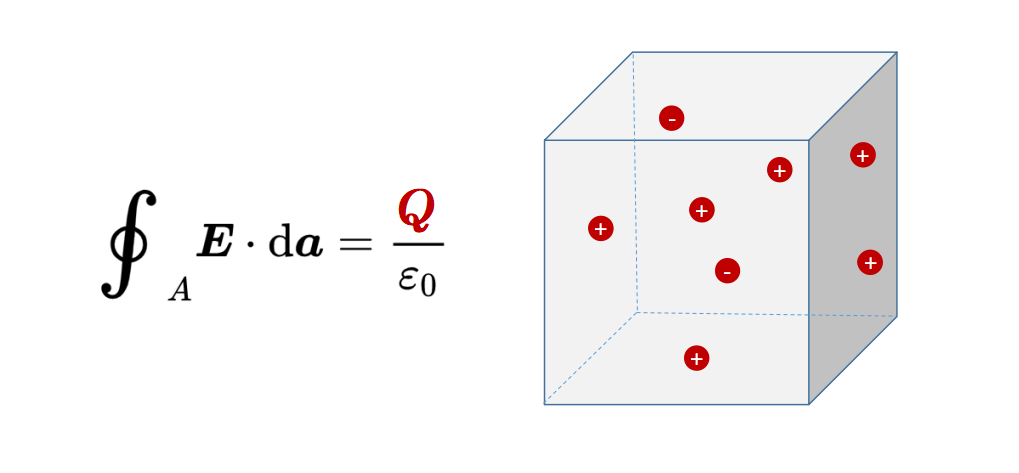
第一个麦克斯韦方程表明,通过封闭表面A的电通量Phi对应于被这个表面包围的电荷Q。
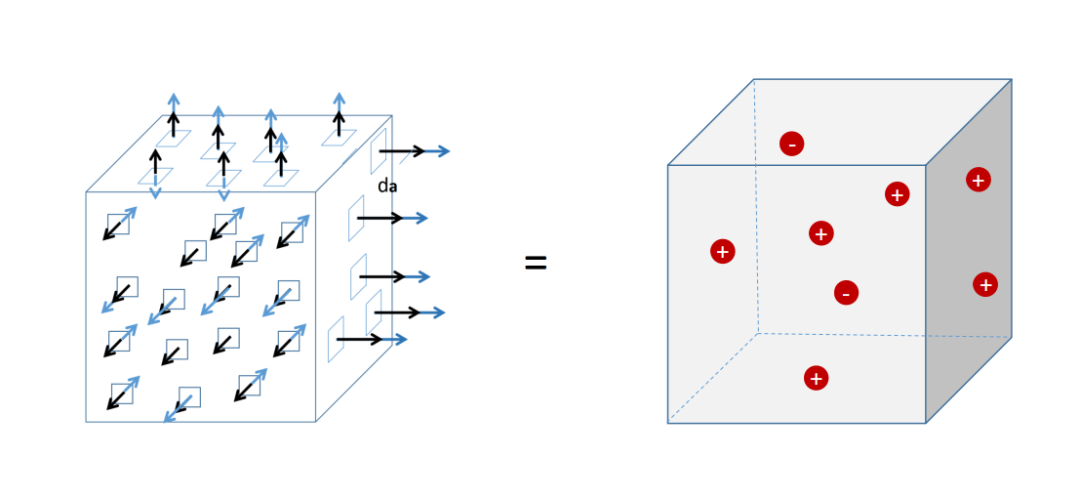
顺便说一句:库仑定律是第一个麦克斯韦方程的一个特例。
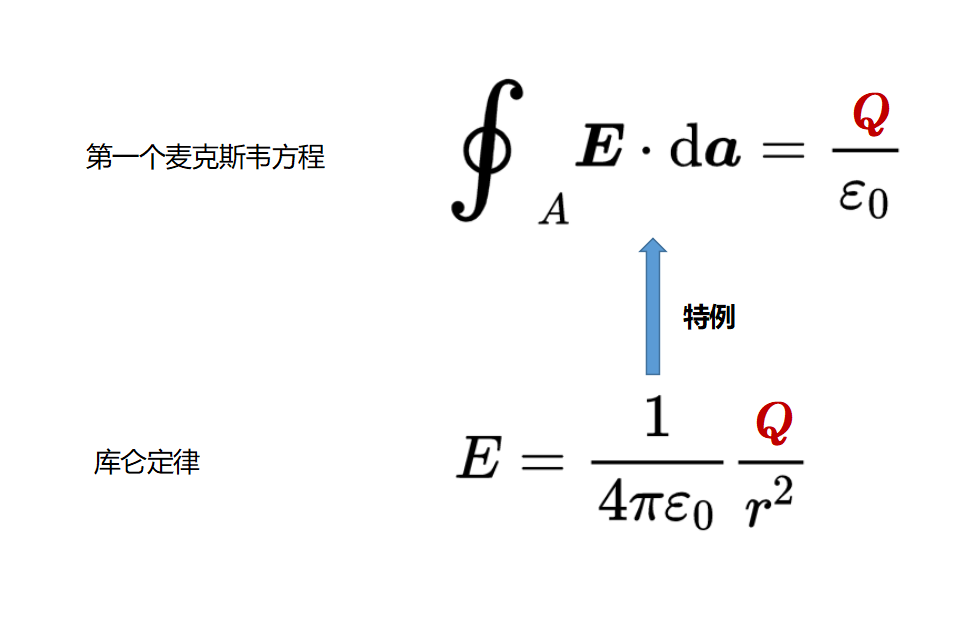
利用之前学习的散度积分定理,它结合了体积积分和表面积分:
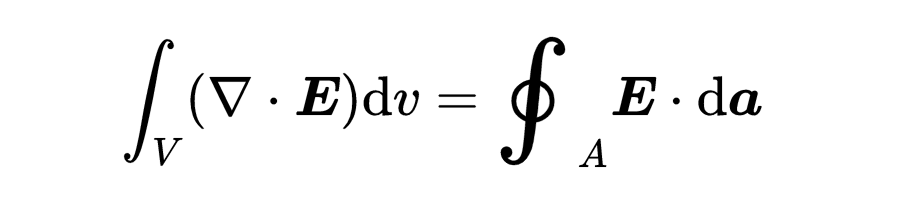
第一个麦克斯韦方程左侧的表面积分可以被替换为电场散度的体积积分,
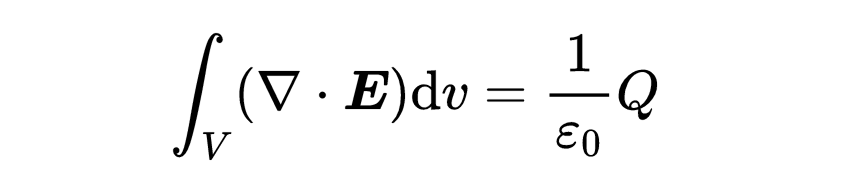
封闭的电荷Q也可以用体积积分来表示。根据定义,电荷密度是电荷除以体积。将体积移到另一侧,那么就有了'Q等于rho乘以V'。体积V通常可以写成体积积分的形式。

也就是说,电荷密度rho对体积V的体积积分是封闭在该体积内的电荷。这使得麦克斯韦方程的右侧变成了一个体积积分。
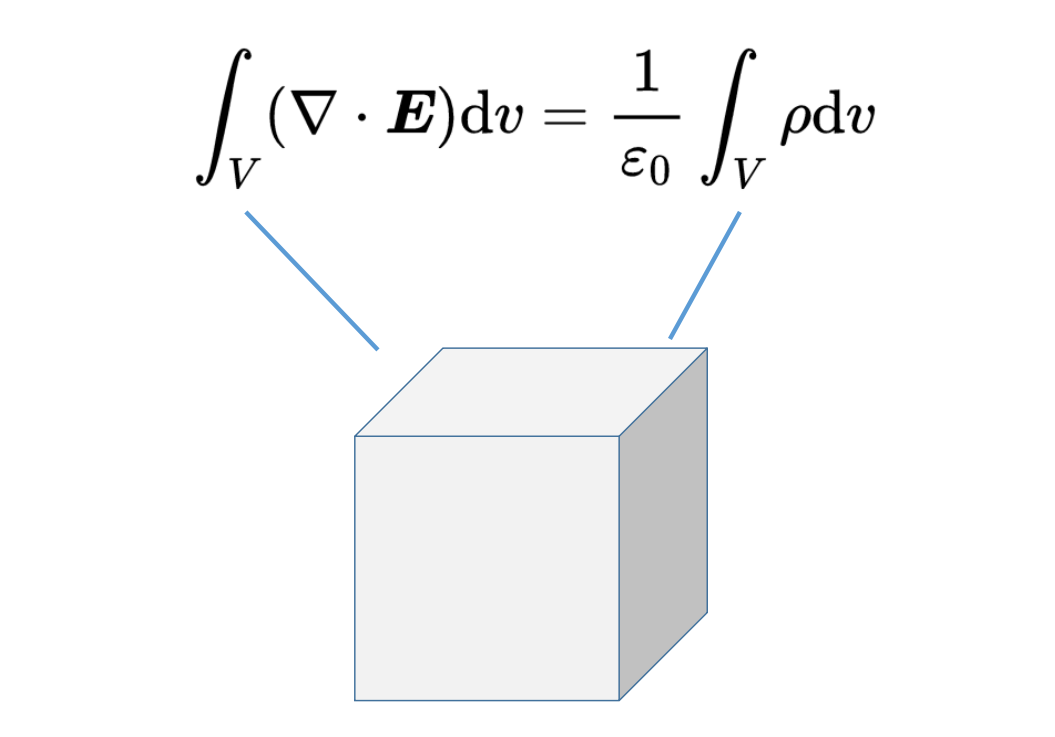
如你所见,我们在两边都对同一个体积V进行了积分。为了满足这个方程对于任意选择的体积V,两边的被积函数必须相等。现在你已经发现了第一个麦克斯韦方程的微分形式:
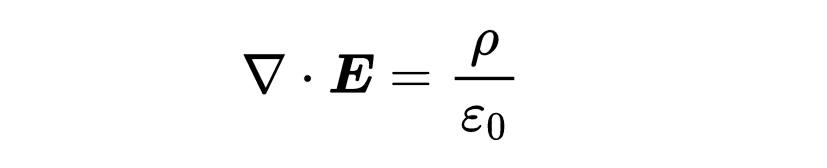
在微分形式的左侧,你可以看到电场的散度。你知道在空间的一个特定点上,它可能是正的、负的或者零。
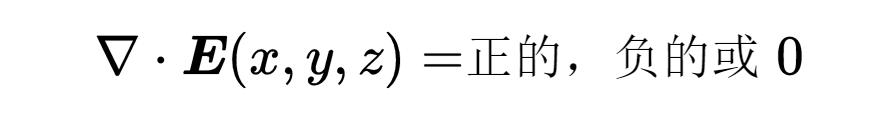
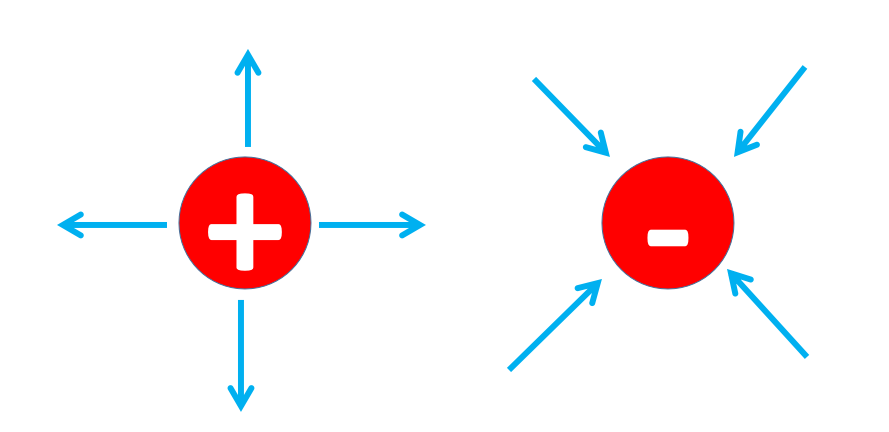
散度的符号决定了在考虑的空间点上的电荷的类型。如果散度是正的,那么在这个空间点上的电荷密度rho就是正的,因此电荷也是正的。因此,在这个空间点有一个正电荷,这是电场的来源。如果散度是负的,那么电荷密度rho就是负的,因此电荷也是负的。在这个空间点上,因此有一个负电荷,这是电场的汇流点。
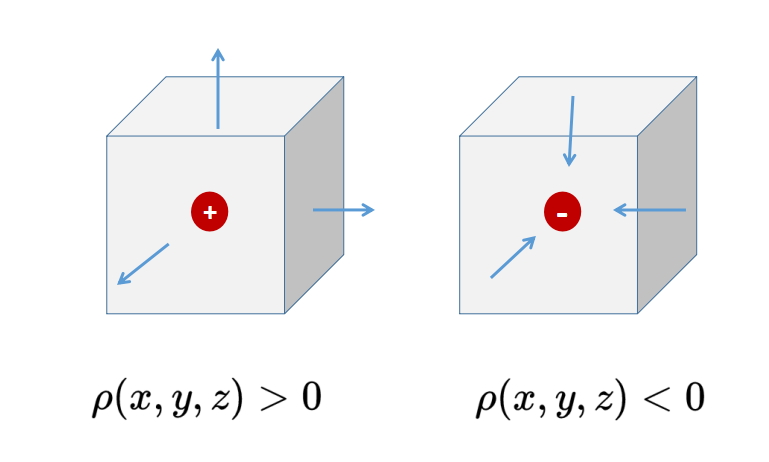
如果散度为零,那么电荷密度rho也为零。在空间的这个点,要么没有电荷,要么正电荷和负电荷的数量一样多,因此这个点的总电荷被抵消了。
第一个麦克斯韦方程(微分形式)声明电荷是电场的源和汇。电荷生成电场!
第二个麦克斯韦方程
这是第二个麦克斯韦方程的积分形式,
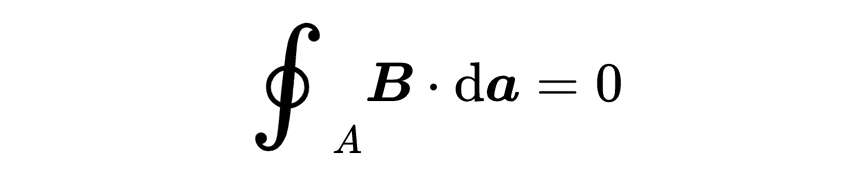
这个方程没有什么陌生的内容。所有的东西现在应该看起来都很熟悉。在等式左侧,你看到了一个关于A的面积积分。这次不是电场的积分,而是磁场B的积分。根据等式,通过封闭表面A的磁通量总是等于零。
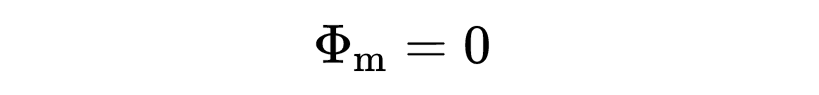
第二个麦克斯韦方程表明,总是有和进入表面的磁场矢量一样多的磁场矢量从表面出来。
通过散度积分定理,面积积分可以转换为体积积分;这样,磁场的散度就起到作用了。这个积分应该是零。对于任何体积V的积分,只有在被积函数为零的情况下才总是零。
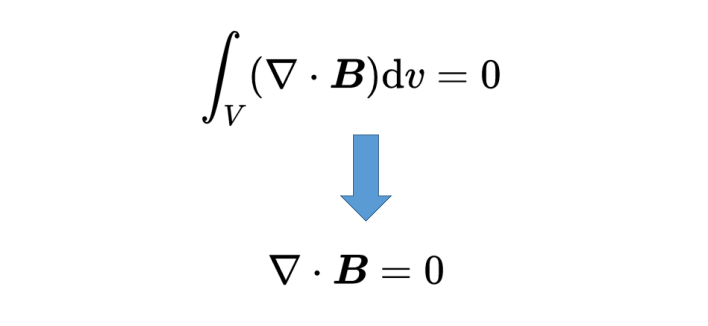
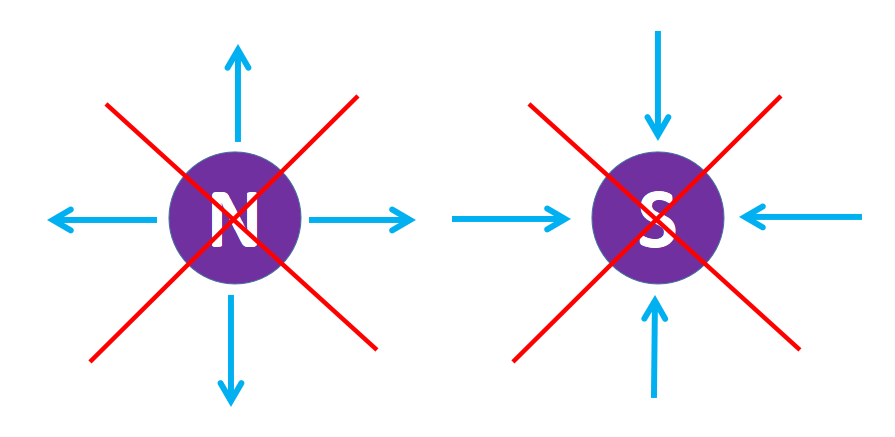
因此,第二个麦克斯韦方程以其微分形式出现:“B的散度等于零”。如果散度为零,这意味着在空间的每一个点(x, y, z)上,要么没有磁电荷(也称为磁单极子),要么正磁电荷和负磁电荷的数量一样多,所以那一点的总电荷抵消了,就像一个理想的磁偶极子,它总是有一个北极和一个南极。
北极对应正磁电荷,南极对应负磁电荷。由于没有磁单极子,所以没有分离的磁场源和汇。第二个麦克斯韦方程的微分形式表明,没有磁单极子产生磁场。只有磁偶极子可以存在。
第二个麦克斯韦方程,就像其他麦克斯韦方程一样,是一个实验结果。也就是说,如果有一天发现了一个磁电荷,那么第二个麦克斯韦方程就必须被修改。然后麦克斯韦方程将看起来更加对称,更加美丽!
第三个麦克斯韦方程(法拉第感应定律)
这是第三个麦克斯韦方程在积分形式下的样子,
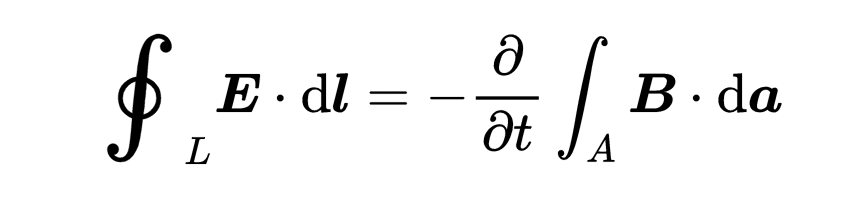
你可能已经知道第三个麦克斯韦方程,也就是法拉第的感应定律。这就是感应定律的最一般形式。
左侧是电场E沿一个封闭线L的线积分,它形成表面A。这个积分把沿着线L运动的电场的所有部分都加起来。这个积分对应于沿着线L的电压U。
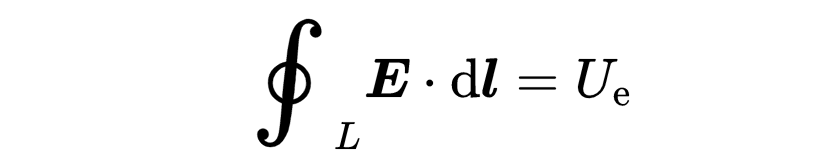
在右侧有一个关于任意表面A的磁场B的面积积分。这个积分对应于通过表面A的磁通量Φ。这个磁通量是相对于时间t进行微分的。
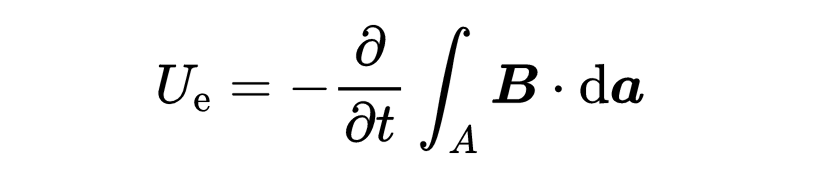
磁通量的时间导数表示随着时间的流逝磁通量变化了多少。所以它是磁通量的时间变化。
磁通量的变化越大,旋转电场就越大。
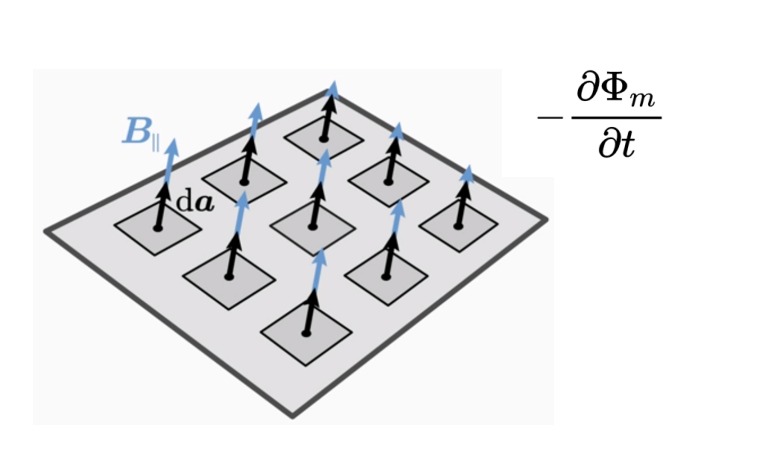
负号考虑了旋转的方向。如果磁通量的变化是正的,电压就是负的。如果磁通量的变化是负的,电压就是正的。电压和磁通量的变化在行为上是相反的。负号保证了能量守恒。也许你知道这个名字:楞次定律(lenz's law)。
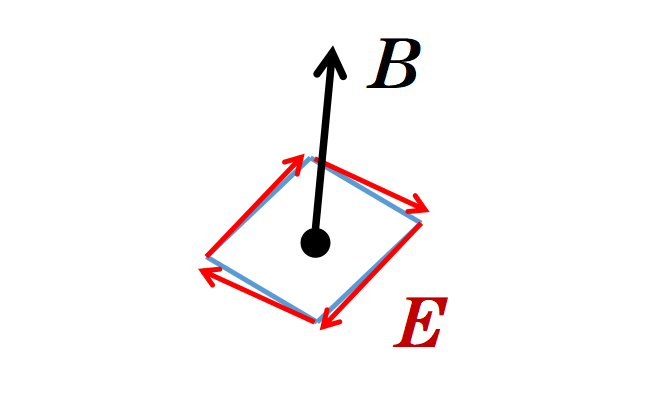
正如你所看到的,根据这个麦克斯韦方程,旋转电场产生了随时间变化的磁场,反之亦然。
所以让我们总结一下:第三个麦克斯韦方程表明,沿着一个封闭线的电压对应于通过该线边界的表面的磁通量的变化。换句话说,通过表面A的磁通量的变化会在A的边缘产生电压。
让我们考虑另一个重要的特殊情况。如果磁场不随时间变化,那么麦克斯韦方程的右侧就会被消除。
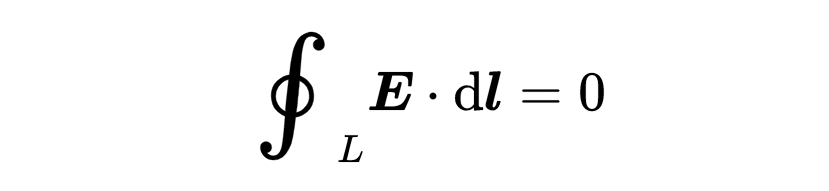
然后这个方程就表明,沿着一个封闭线的电压总是零。所以只有当磁场不随时间变化时,才没有旋转电场。
如果一个电子通过封闭线L,它的能量不会改变,因为,电压表示一个电荷在通过一条线时获得或失去的能量。在这种情况下,电压为零。因此没有能量变化。
使用旋度积分定理,可以将积分形式转化为微分形式。这个定理将线积分与面积积分相连。为此,只需将线积分替换为面积积分。这就引出了E的旋度。
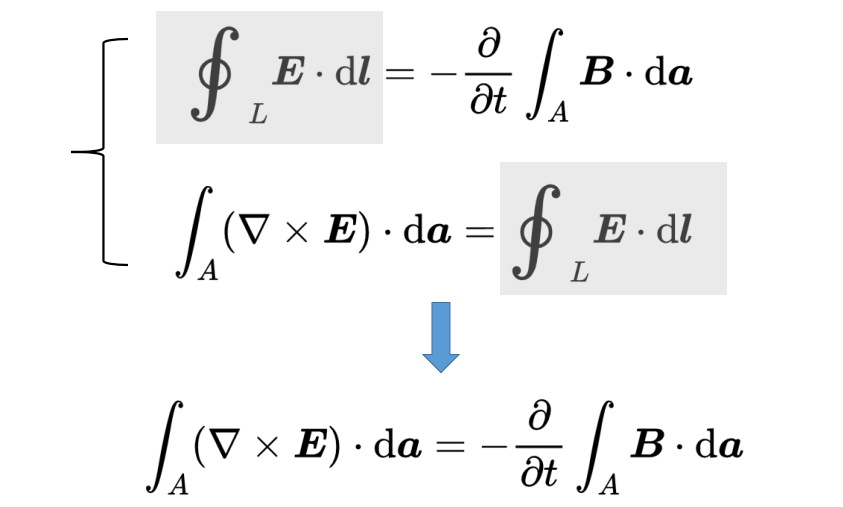
在另一边,你可以把时间导数放进积分里,
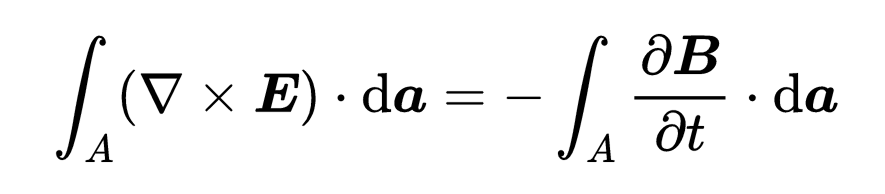
由于方程对任何表面A都适用,所以两边的被积函数必须相等。就这样,你发现了第三个麦克斯韦方程的微分形式:“E的旋度等于磁场的负时间导数”,
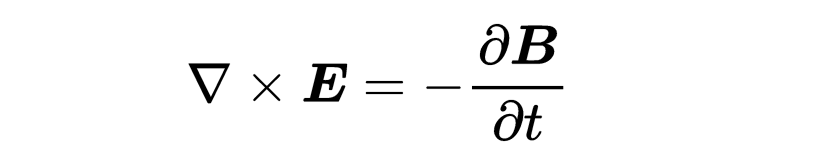
微分形式的第三个麦克斯韦方程表明,一个变化的磁场B会产生一个旋转的电场E,反之亦然,以保证能量守恒。
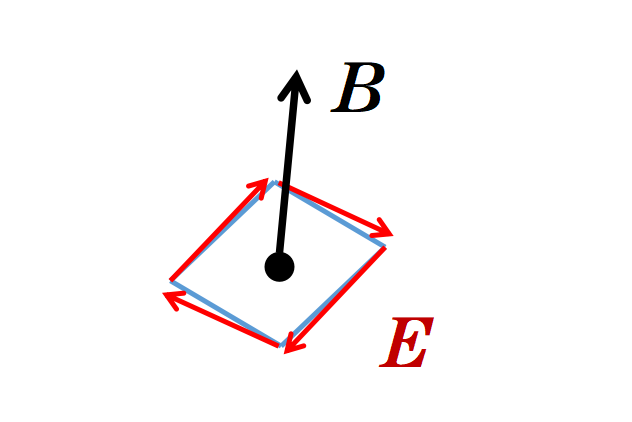
我们现在转向第四个,也是最后一个麦克斯韦方程。
第四个麦克斯韦方程
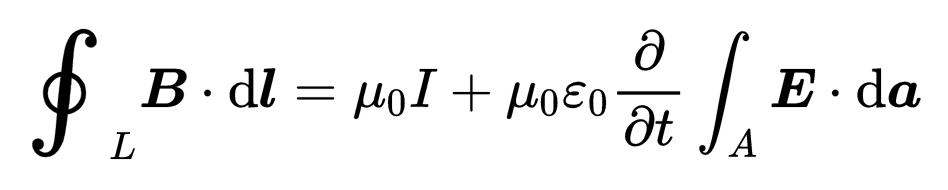
左侧的积分是什么类型的?沿封闭线L的磁场B的线积分,这就是磁电压U的定义,
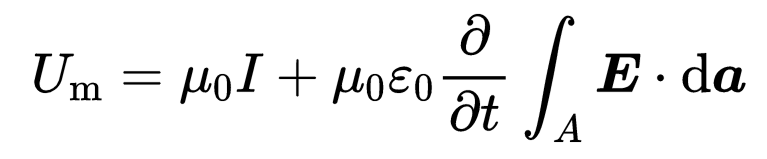
右侧有电场常数Epsilon_0和磁场常数Mu_0。它们确保了麦克斯韦方程两侧的单位是一样的:
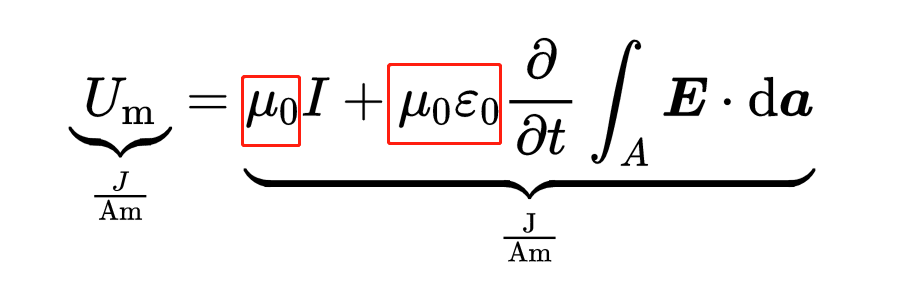
此外,这里还有一些新的东西,那就是电流I。当电荷沿导体流动时,它们会产生一个电流I。此外还有另一个加数:
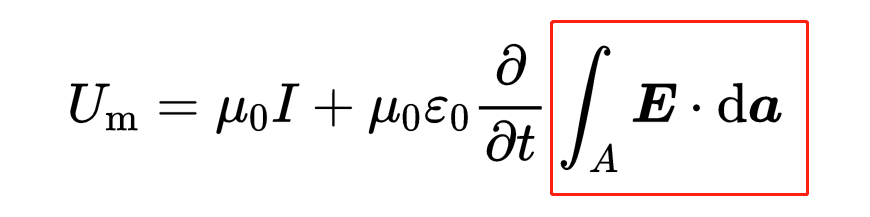
我们知道电场的面积积分,就是通过表面A的电通量。此外,电通量前面还有一个时间导数。所以整个式子就是电通量的时间变化。
总结一下:右侧有两个加数:一个由电流贡献,一个由电通量的变化贡献。
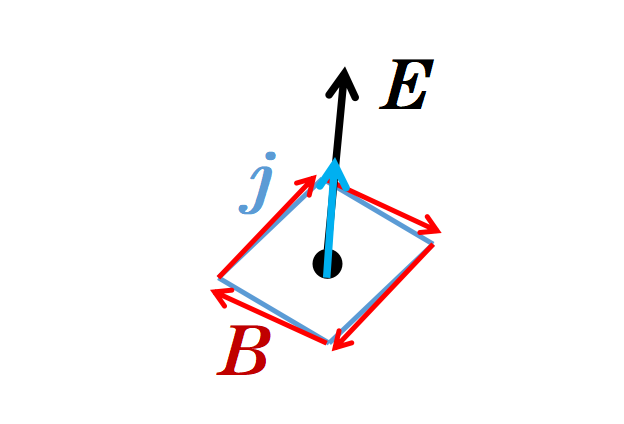
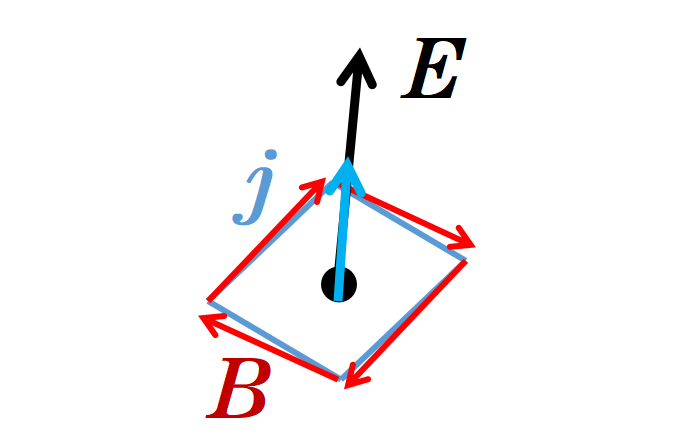
因此,第四个麦克斯韦方程表明,旋转磁场首先由穿过面积A的电流产生,其次由变化的电场产生。
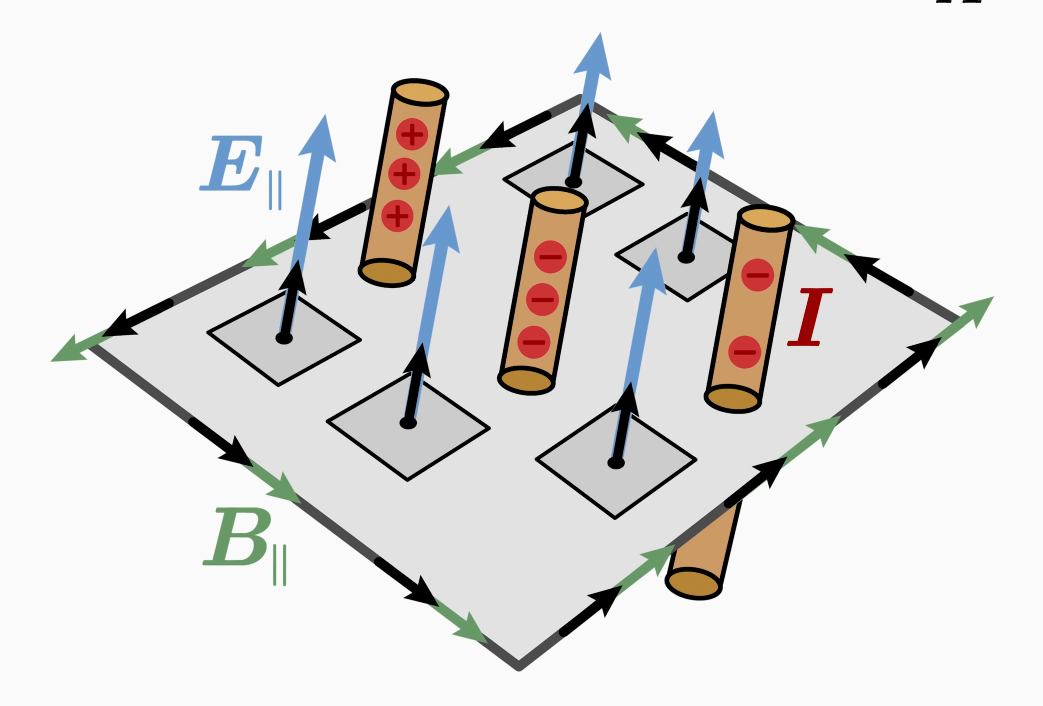
让我们现在推导出微分形式。利用旋度积分定理,可以将线积分转化为面积积分,从而引入磁场B的旋度。
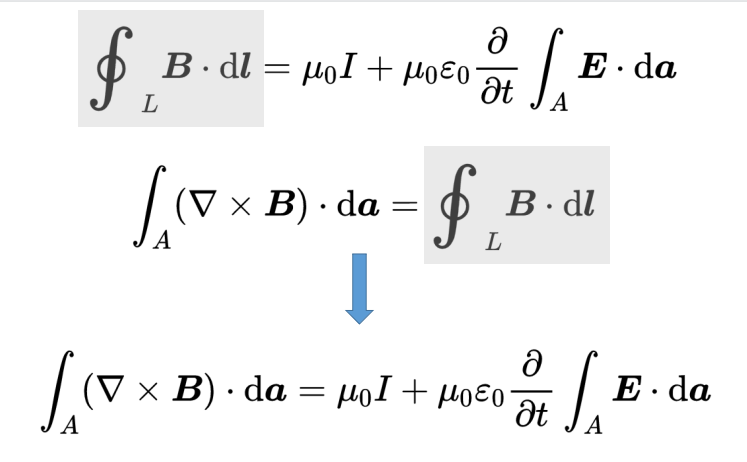
现在我们需要用面积积分来表示电流I,这样我们在右边就能得到一个单一的被积函数。我们可以简单地使用电流密度j来做到这一点,
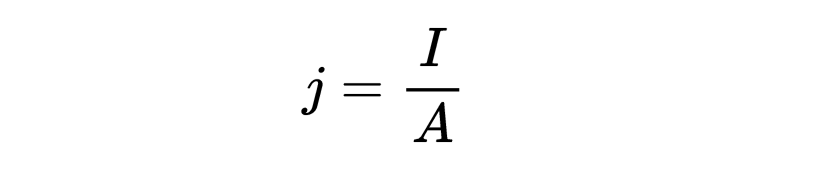
它表示电流流过的区域的电流。因此,电流也可以写成电流密度j在表面A上的面积积分,
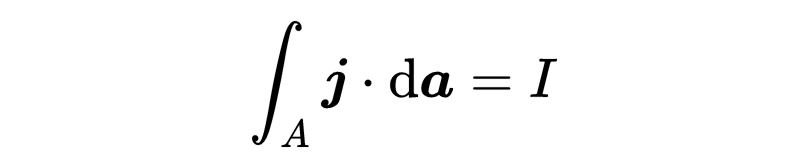
注意在积分中,电流密度与da元素的标量积被取出。所以我们只选取了电流密度矢量与da元素平行的部分。只有电流密度的这个平行部分才对通过面A的电流有贡献。你可以将时间导数放进积分中,
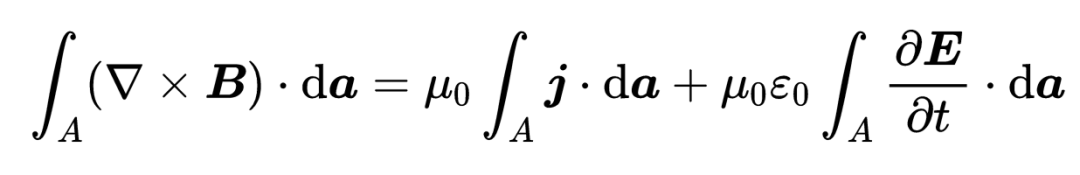
现在,由于在同一个表面A上积分,所以可以将两个面积积分合并为一个,
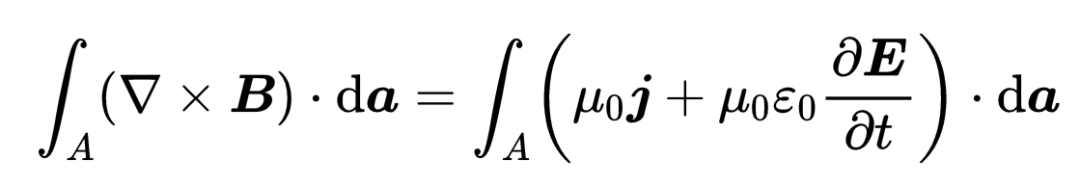
为了满足对任何表面A的方程,两边的被积函数必须相等。我们已经找到了第四个麦克斯韦方程的微分形式:“B的旋度等于mu_zero乘以I + mu_zero epsilon_zero乘以电场随时间的变化”:
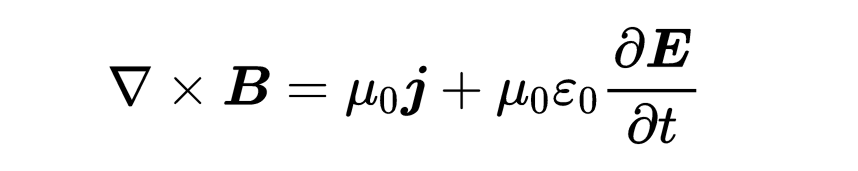
微分形式因此表明,在空间中的一个点处,磁场B的旋度有两种原因:电流密度j和在这个点处变化的电场。
总结
让我们以紧凑的形式(微分形式),总结电动力学的四个麦克斯韦方程。
第一个麦克斯韦方程:E的散度等于电荷密度除以epsilon_zero。电荷产生电场。
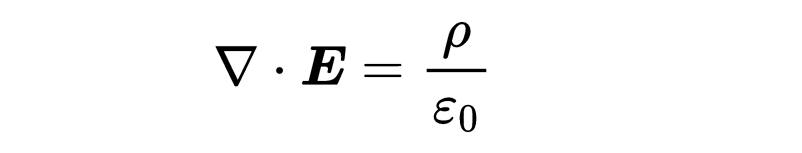
第二个麦克斯韦方程:B的散度等于零。没有磁单极子。
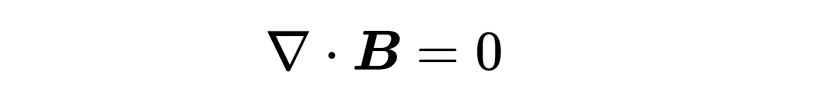
第三个麦克斯韦方程:E的旋度等于磁场的负时间导数。一个变化的磁场创造一个旋转的电场,反之亦然。
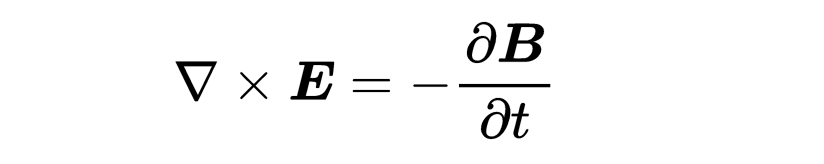
第四个麦克斯韦方程:B的旋度等于mu_zero乘以I + mu_zero epsilon_zero乘以电场随时间的变化。电流和变化的电场生成磁场。
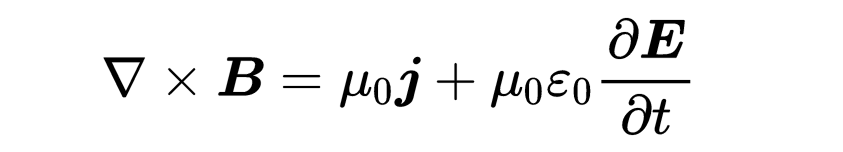
-
电动汽车
+关注
关注
156文章
12231浏览量
232951 -
磁场
+关注
关注
3文章
897浏览量
24357 -
WIFI
+关注
关注
81文章
5320浏览量
205428 -
无线电
+关注
关注
60文章
2154浏览量
117017 -
麦克斯韦
+关注
关注
0文章
19浏览量
5768
原文标题:深度解析麦克斯韦方程
文章出处:【微信号:mcu168,微信公众号:硬件攻城狮】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
麦克斯韦方程组究竟带来了什么
麦克斯韦Maxwell方程组是怎么来的
电磁场理论之麦克斯韦方程组论文的详细资料免费下载
追逐麦克斯韦方程组与电磁波理论
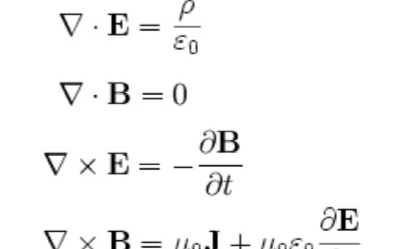
麦克斯韦方程组的详细资料说明





 深度解析麦克斯韦方程
深度解析麦克斯韦方程
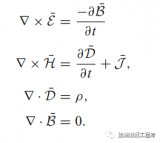










评论