0. 前言
之前上模式识别课程的时候,老师也讲过 MLP 的 BP 算法, 但是 ppt 过得太快,只有一个大概印象。后来课下自己也尝试看了一下stanford deep learning的 wiki, 还是感觉似懂非懂,不能形成一个直观的思路。趁着这个机会,我再次 revisit 一下。
1. LMS 算法
故事可以从线性 model 说起(顺带复习一下)~在线性 model 里面,常见的有感知机学习算法、 LMS 算法等。感知机算法的损失函数是误分类点到 Target 平面的总距离,直观解释如下:当一个实例点被误分,则调整 w, b 的值,使得分离超平面向该误分类点的一侧移动,以减少该误分类点与超平面的距离,在 Bishop 的 PRML一书中,有一个非常优雅的图展现了这个过程。但是了解了 MLP 的 BP 算法之后,感觉这个算法与 LMS 有点相通之处。虽然从名字上 MLP 叫做多层感知机,感知机算法是单层感知机。
LMS (Least mean squares) 算法介绍比较好的资料是 Andrew Ng cs229 的Lecture Notes。假设我们的线性 model 是这样的:
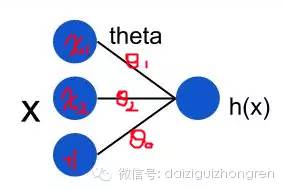
在上面这个模型中,用公式可以表达成:
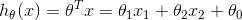
如何判断模型的好坏呢?损失函数定义为输出值 h(x) 与目标值 y 之间的“二乘”:
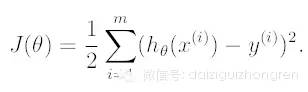
对偏导进行求解,可以得到:
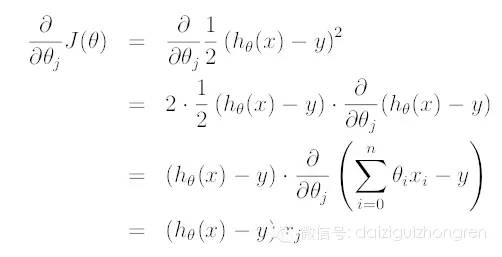
如果要利用 gradient descent 的方法找到一个好的模型,即一个合适的 theta 向量,迭代的公式为:
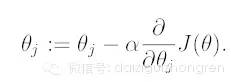
所以,对于一个第 i 个单独的训练样本来说,我们的第 j 个权重更新公式是:
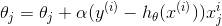
这个更新的规则也叫做 Widrow-Hoff learning rule, 从上到下推导下来只有几步,没有什么高深的理论,但是,仔细观察上面的公式,就可以发现几个 natural and intuitive 的特性。
首先,权重的更新是跟 y - h(x) 相关的,如果训练样本中预测值与 y 非常接近,表示模型趋于完善,权重改变小。反之,如果预测值与 y 距离比较远,说明模型比较差,这时候权重变化就比较大了。
权重的变化还与 xi 也就是输入节点的值相关。也就是说,在同一次 train 中,由于 y - h(x) 相同, 细线上的变化与相应的输入节点 x 的大小是成正比的(参考最上面的模型图)。这中间体现的直观印象就是:残差的影响是按照 xi 分配到权重上去滴,这里的残差就是 h(x) - y。
LMS 算法暂时先讲到这里,后面的什么收敛特性、梯度下降之类的有兴趣可以看看 Lecture Notes。
2. MLP 与 BP 算法
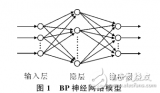
前面我们讲过logistic regression, logistic regression 本质上是线性分类器,只不过是在线性变换后通过 sigmoid 函数作非线性变换。而神经网络 MLP 还要在这个基础上加上一个新的nonlinear function, 为了讨论方便,这里的 nonlinear function 都用 sigmoid 函数,并且损失函数忽略 regulization term, 那么, MLP 的结构就可以用下面这个图来表示:
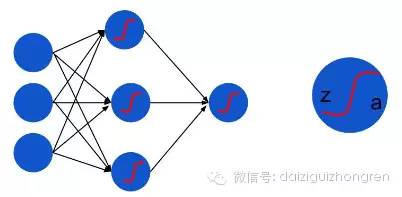
z: 非线性变换之前的节点值,实际上是前一层节点的线性变换
a: 非线性变换之后的 activation 值
a=f(z): 这里就是 sigmoid function
现在我们要利用 LMS 中的想法来对这个网络进行训练。
假设在某一个时刻,输入节点接受一个输入, MLP 将数据从左到右处理得到输出,这时候产生了残差。在第一小节中,我们知道, LMS 残差等于 h(x) - y。MLP 的最后一层和 LMS 线性分类器非常相似,我们不妨先把最后一层的权重更新问题解决掉。在这里输出节点由于增加了一个非线性函数,残差的值比 LMS 的残差多了一个求导 (实际上是数学上 chain rule 的推导):
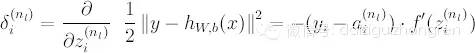
得到残差,根据之前猜想出来的规律( - -!), 残差的影响是按照左侧输入节点的 a 值大小按比例分配到权重上去的,所以呢,就可以得到:
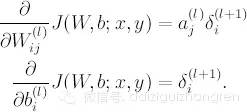
如果乘以一个 learning rate, 这就是最后一层的权重更新值。
我们在想,要是能得到中间隐层节点上的残差,问题就分解成几个我们刚刚解决的问题。关键是:中间隐层的残差怎么算?
实际上就是按照权重与残差的乘积返回到上一层。完了之后还要乘以非线性函数的导数( again it can be explained by chain rule):
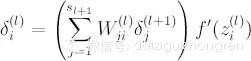
得到隐层的残差,我们又可以得到前一层权重的更新值了。这样问题就一步一步解决了。
最后我们发现,其实咱们不用逐层将求残差和权值更新交替进行,可以这样:
先从右到左把每个节点的残差求出来(数学上表现为反向传导过程)
然后再求权重的更新值
更新权重
Q:这是在 Ng 教程中的计算过程, 但是在有些资料中,比如参考资料 [2],残差和权值更新是逐层交替进行的,那么,上一层的残差等于下一层的残差乘以更新后的权重,明显,Ng 的教程是乘以没有更新的权重,我觉得后者有更好的数学特性,期待解疑!
用一张粗略的静态图表示残差的反向传播:
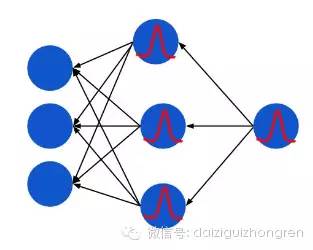
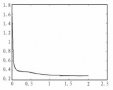
红色的曲线就是对 sigmoid function 的求导,和高斯分布非常相似。
用一张动态图表示前向(FP)和后向(BP)传播的全过程:
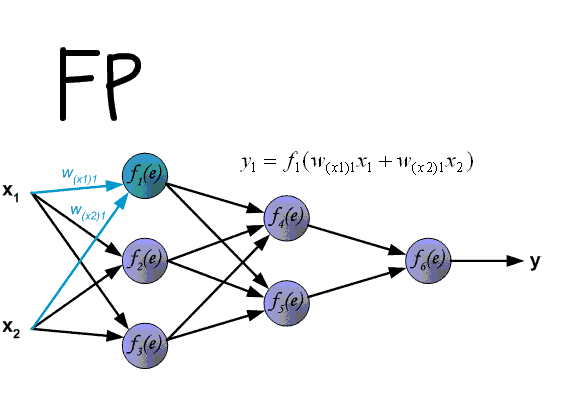
OK,现在 BP 算法有了一个直观的思路,下面,将从反向传导的角度更加深入地分析一下 BP 算法。
审核编辑:刘清
-
神经网络
+关注
关注
42文章
4779浏览量
101097 -
变换器
+关注
关注
17文章
2109浏览量
109496 -
LMS算法
+关注
关注
1文章
19浏览量
10276 -
线性分类器
+关注
关注
0文章
3浏览量
1442 -
MLP
+关注
关注
0文章
57浏览量
4273
原文标题:[干货]BP 算法之一种直观的解释
文章出处:【微信号:vision263com,微信公众号:新机器视觉】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
如何设计BP神经网络图像压缩算法?
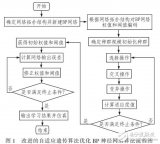
一种改进的自适应遗传算法优化BP神经网络




 BP神经网络算法 BP算法之一种直观的解释
BP神经网络算法 BP算法之一种直观的解释











评论