周期信号的傅里叶变换和非周期信号的傅里叶变换有何关系？

我们从复指数形式的傅里叶级数的系数出发：

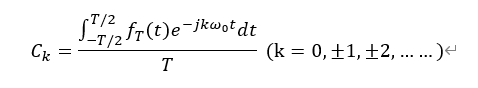
其中，f T (t)为周期信号，我们将周期T乘到右边，得到：

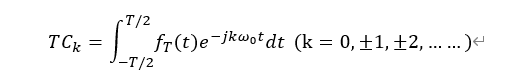
从上一讲我们知道，周期信号的幅度谱和相位谱是在kω 0 （k=0,±1,±2,……）上离散的点取值，那么，ω0也可以表示为离散点的间隔，记作∆ω。同时从上述表达式可以看出，TCk是一个变量为kω0的函数（原因很简单，表达式是对t积分，积分完t就没了，那么只有kω0这个变量），而kω0也可以记作k∆ω，表达式可以换成：

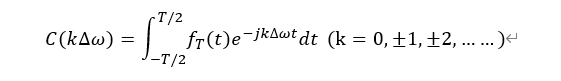
当T—>ꚙ时，f T (t) —>f(t)，而∆ω—> dω，k∆ω—> ω：

那么就可以得到傅里叶变换，即：

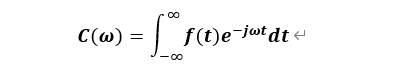
而从上述表达式转化中可以看出，TCk是一个变量为k∆ω的函数，那么当T—>ꚙ时， TC k =C k /f，f—>0，即C(ω)为单位频率的表达式，因此把C(ω)称之为频谱密度函数，也就是我们常说的频谱函数。

我们再看傅里叶逆变换：

我们从周期信号的复指数形式傅里叶级数出发：

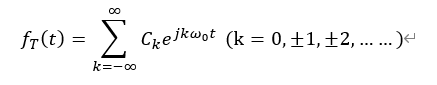
根据上面推导傅里叶变换的结论，上面表达式可以转换为：

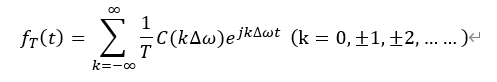
而∆ω=2π/T，则：

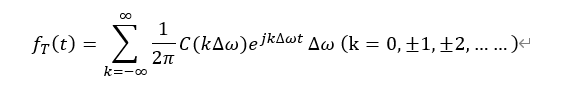
当T—>ꚙ时，f T (t) —>f(t)，∆ω—> dω，k∆ω—> ω，则可以得到傅里叶逆变换的表达式：

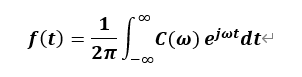
至此，傅里叶变换和傅里叶逆变换的表达式推导完毕。从推导过程可以看出，我们从傅里叶级数出发，利用了T—>ꚙ这个条件，C(ω)=C(k∆ω) =TCk **，**从而推导出傅里叶变换，换句话说，傅里叶变换是周期趋于无穷大的周期信号的傅里叶级数。

接着我们看第二个问题：傅里叶变换的物理意义。

我们还是从傅里叶变换和傅里叶级数的关系入手：

傅里叶变换：

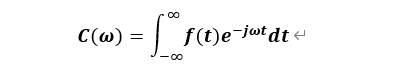
傅里叶逆变换：

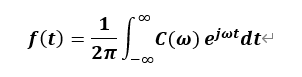
我们再结合傅里叶级数的表达式：

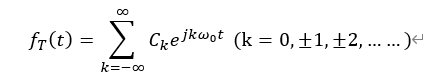
从上一篇可知，傅里叶级数的物理意义是：任意一个周期信号，都可以用该复指数函数集{e^jk^ ^ω0t^ }(k=0,±1, ±2,……)来表示；而Ck为f(t)在复指数函数集{e^jk^ ^ω0t^ } (k=0,±1, ±2,……)各个正交基的坐标，即C~k~描述了各频率分量kω ~0~ (k=0,±1, ±2,……)之间的相对关系，其中|C ~k~ |~ω的关系图称为幅度谱，代表各频率分量kω~0~ (k=0,±1, ±2,……)的绝对大小，ϕ ~k~ ~ ω称为相位谱，代表各频率分量kω~0~ (k=0,±1, ±2,……)的相对位置。

那么类推可知， 傅里叶变换的物理意义是：任意一个非周期信号，都可以用复指数函数集{e^j^ ** ^ωt^ }** 来表示（其中ω无限趋近于0），而C(ω)为f(t)在复指数函数集{e^j^ ** ^ωt^ }** 各个正交基的坐标，即C(ω)描述了各频率分量之间的相对关系，其中| C(ω)|~ω的关系图称为幅度谱，代表各频率分量的绝对大小，ϕ ω ~ ω称为相位谱，代表各频率分量的相对位置。

两者的区别用下图表示，就一目了然了，由于非周期信号中的ω，是一个无限趋近于0的变量，反映在图中，即每根正交基向量之间的间距无限小，这也再一次说明了上面那个结论：傅里叶变换是周期趋于无穷大（频率趋于无穷小）的周期信号的傅里叶级数。

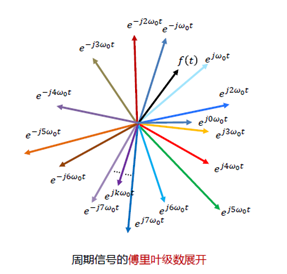
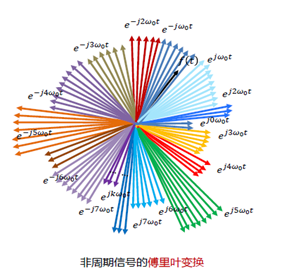
基于上面的物理意义，就很容易理解“ 非周期信号的频谱是连续的，周期信号的频谱是离散的 ”这句话的含义。

接下去看第三个问题，周期信号的傅里叶变换和傅里叶级数之间的关系？

先了解三个典型信号的傅里叶变换对（利用傅里叶变换的表达式很容易推出，此处不详细阐述）：

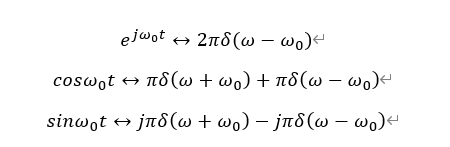
我们利用这三个典型信号的傅里叶变换对，从复指数形式的傅里叶级数出发：

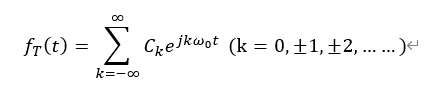
因为：

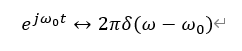
因此：

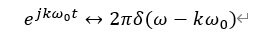
从而可以得出周期信号的傅里叶变换：

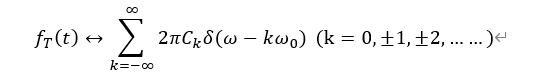
我们知道，周期信号的傅里叶级数是为了将周期信号从时域转换成频域进行分析，也就是周期信号的频谱，而周期信号的傅里叶变换也是将周期信号从时域转换成频域进行分析。 那么从表达式上看，一个是Ck，一个是2****πCkδ(ω-kω 0 )，两者完全不一样，实际上是这样的吗？

我们仔细分析可知， δ(ω-kω 0 )其实就是在频率为kω0的一系列冲激信号，也就是说，周期信号的傅里叶变换2πCkδ(ω-kω 0 )只是在频率为kω0才有数值，且数值为2πCk，其他频率皆为0。而傅里叶级数Ck我们之前分析过它的幅度谱和相位谱，只是在kω0的地方才有数值，而两者之间的幅度谱相差一个2π的倍数，就是之前推导傅里叶变换时，C k =C(ω) * ω/2π****而产生的，因此两者虽然表达式不一样，但本质是一致的。

我们分析出周期信号傅里叶变换和傅里叶级数之间的关系后，就会不由自主地想到另外一个问题：周期信号的傅里叶变换和非周期信号的傅里叶变换存在什么样的关系呢？

分析这个问题，我们可以从一个非周期信号入手，通过周期拓展的方式，将该非周期信号在时间T的周期内进行复制，从而得到一个周期信号，如下图所示。

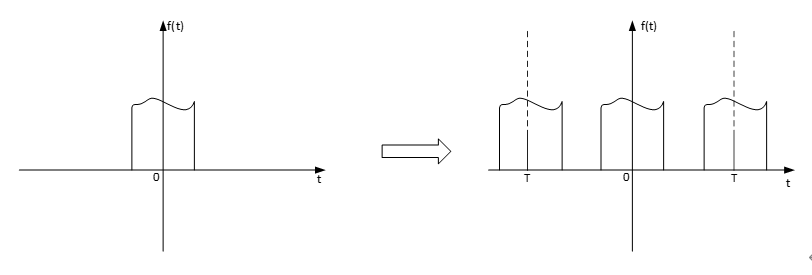
那么怎么进行周期拓展呢？我们应当想到卷积中讲到的信号的分解性质，即一个信号可以分成自身和单位冲激信号的卷积。那么我们只要把单位冲激信号平移周期kT（k=1,2,3,……），再与原本信号进行卷积，相当于把该信号在周期kT上依次进行复制，从而得到周期为T的信号。

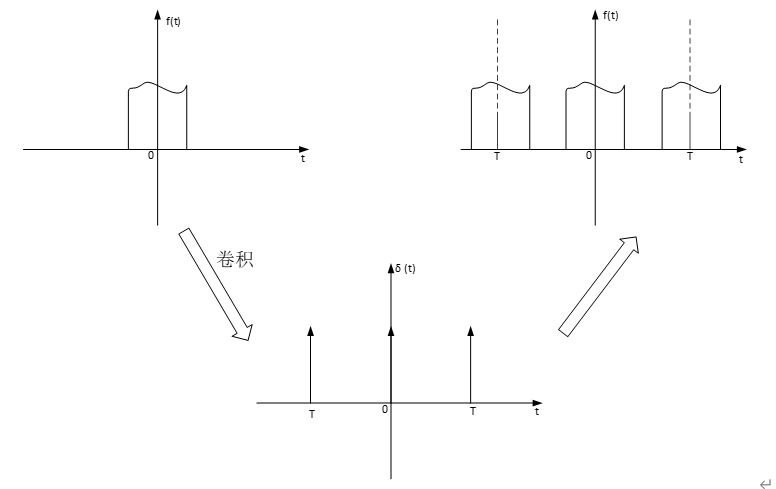
因此我们可以得到：

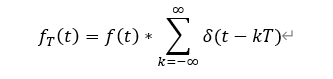
根据δ(t-nT)和卷积的性质，上式进行傅里叶变换：

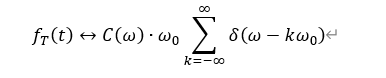
而C(ω)只是在kω0的点上有值，因此上式可以转换为：

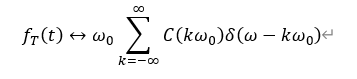
因此，我们从周期拓展的角度出发，同样得到了周期信号的傅里叶变换，从上式可以发现， 一个信号在时域上进行周期T拓展时，所对应的频谱函数只在kω0上有值，也就是说在频域上，频谱函数是离散的， 从周期拓展的角度又一次佐证了 “ 非周期信号的频谱是连续的，周期信号的频谱是离散的 ”这句话。

最后放上自己的一点有趣的思考。

前面我们从复指数形式和周期拓展的形式分别得到了周期信号的傅里叶变换，因为信号是同一个信号，因此两者的傅里叶变换应该相同，因此，我们得出：

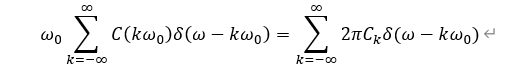
进一步化简可知：

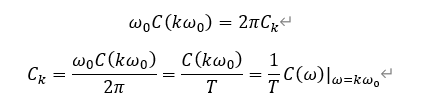
此处我们得到了周期信号傅里叶级数和傅里叶变换的关系，**即傅里叶级数是非周期傅里叶变换在kω 0 **上的取值。

而我们文章一开始推导傅里叶变换的时候，用到的条件之一即为：

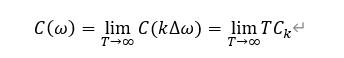
我们从傅里叶级数出发，利用这个条件推导出非周期信号的傅里叶变换，继而推导出周期信号的傅里叶变换，最后利用周期信号的傅里叶变换又反推导回傅里叶级数。