傅里叶变换（对信号分析）（上）
一、引言
时域研究——频域研究
傅里叶级数——采用 三角函数系 （ 互为正交函数 ）进行正交展开
二、周期信号的傅里叶级数分析
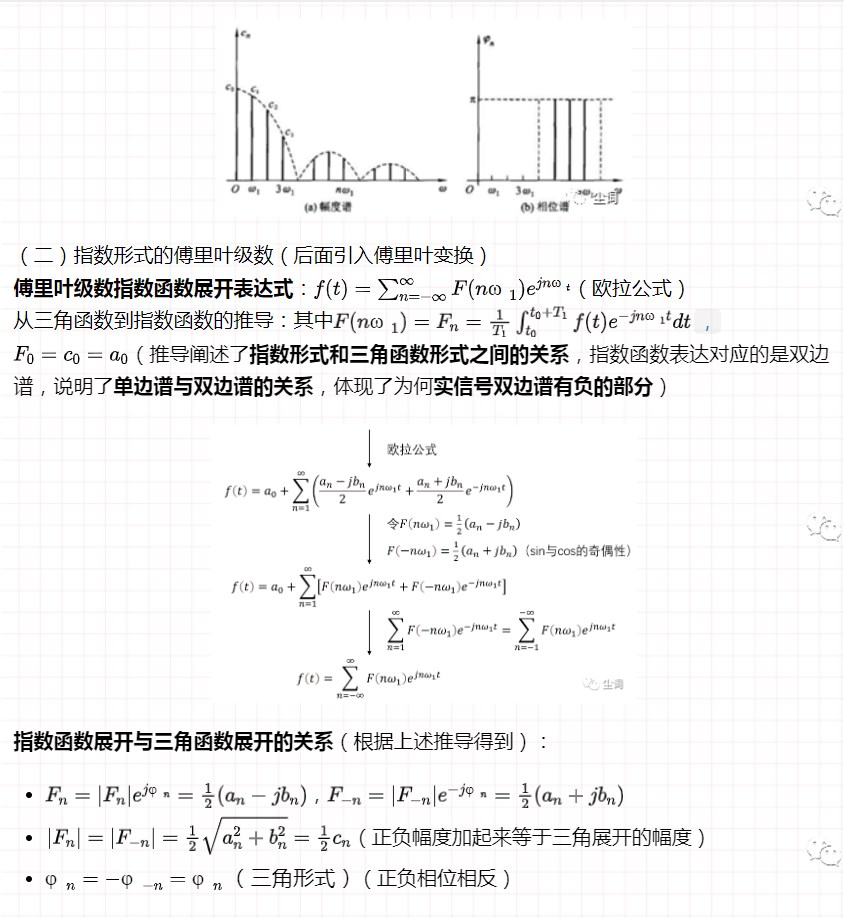
三、典型周期信号的傅里叶级数
（一）周期矩形脉冲信号
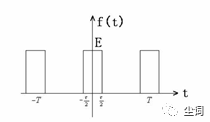
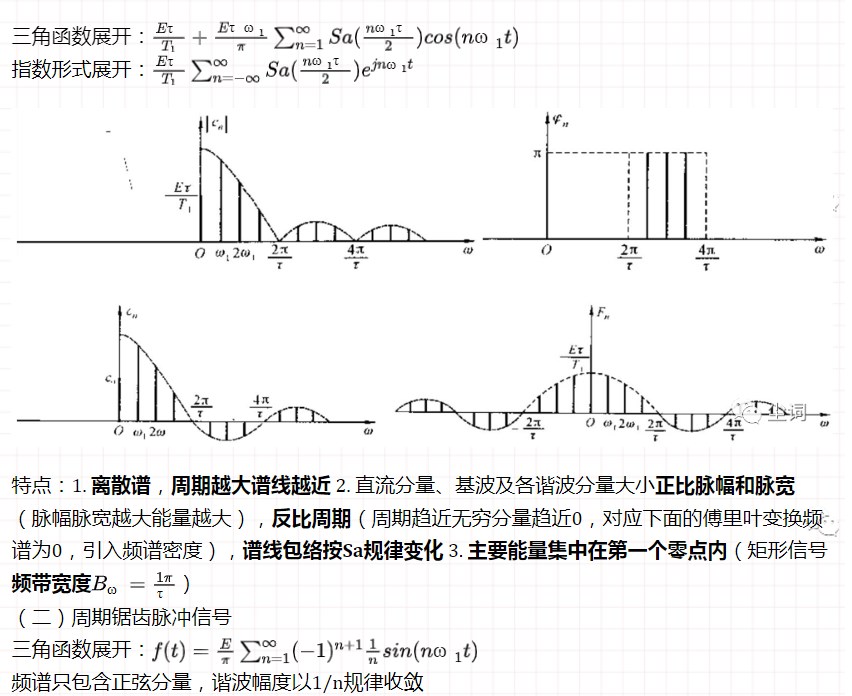
四、傅里叶变换
由傅里叶级数引出傅里叶变换：T→∞时，谱线间隔趋于0，值趋于无限小，由能量守恒得无限多无限小能量之和仍为信号的能量，此时频谱失去意义，故引入频谱密度函数
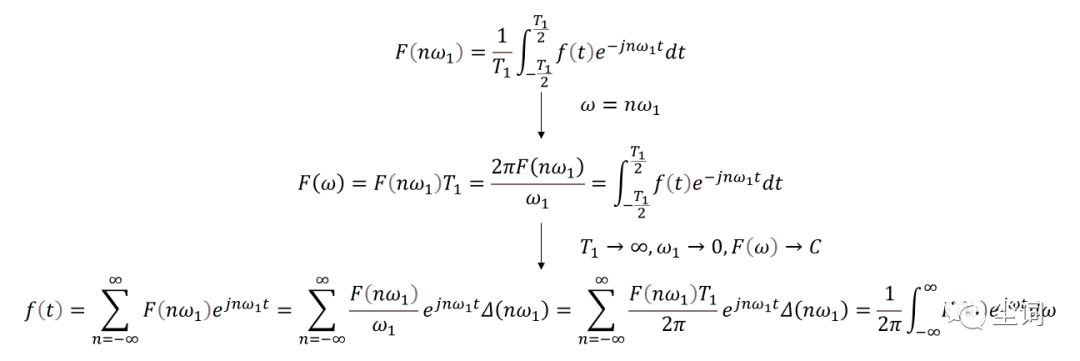
傅里叶变换：
傅里叶逆变换：
三角函数形式傅里叶变换：
（由幅度谱和相位谱奇偶性得到）
幅度双边谱左右对称——幅度频谱偶函数
相位谱关于原点对称——相位频谱奇函数
五、典型非周期信号的傅里叶变换
（一）单边指数信号
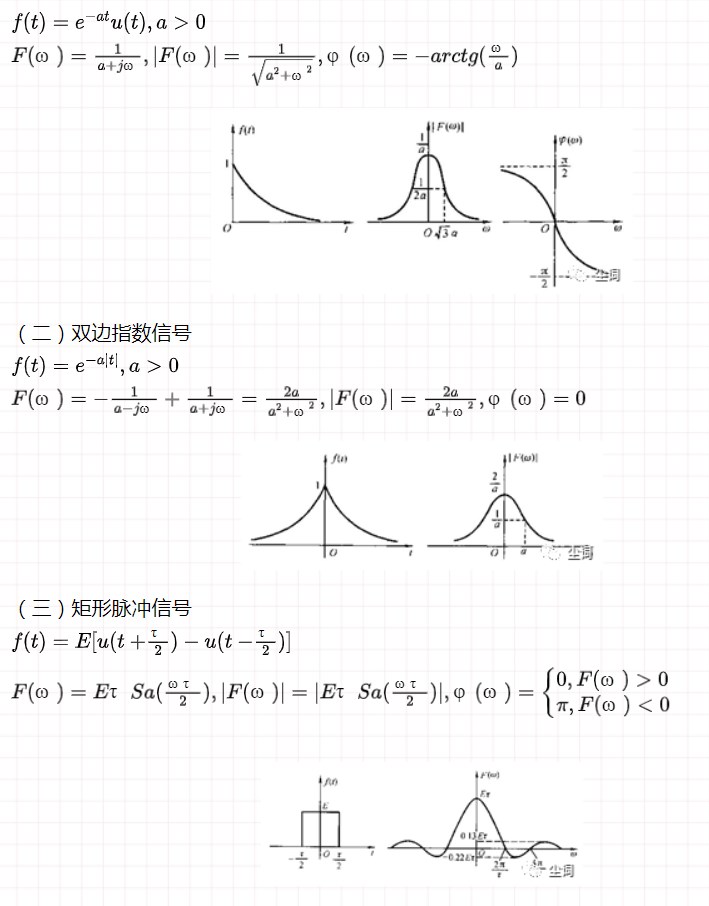
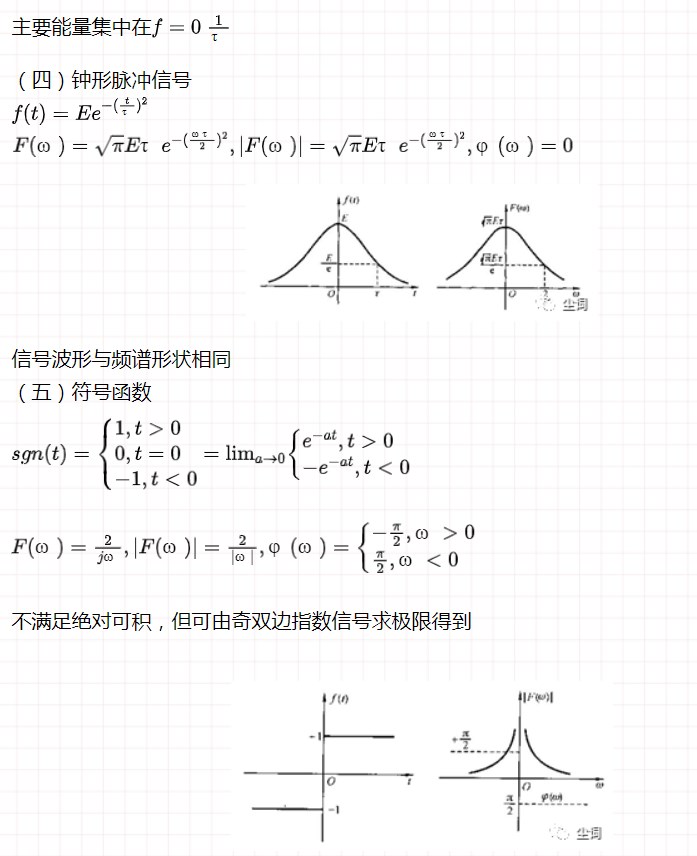
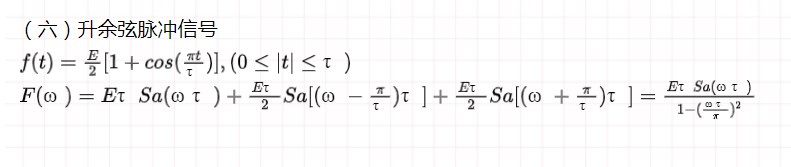
六、冲激函数和阶跃函数的傅里叶变换
（一）冲激函数的傅里叶变换
声明：本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人，不代表电子发烧友网立场。文章及其配图仅供工程师学习之用，如有内容侵权或者其他违规问题，请联系本站处理。
举报投诉
-
变换器
+关注
关注
17文章
2097浏览量
109266 -
低通滤波器
+关注
关注
14文章
474浏览量
47390 -
频谱仪
+关注
关注
7文章
340浏览量
36030 -
傅里叶变换
+关注
关注
6文章
441浏览量
42592 -
直流信号
+关注
关注
0文章
39浏览量
8888
发布评论请先 登录
相关推荐
傅里叶变换，建立信号频谱
从本章开始由时域转入变换域分析，首先讨论傅里叶变换。傅里叶变换是在傅里叶级数正交函数展开的基础上发展而产生的，这方面的问题也称为傅里叶
发表于 08-05 11:49
•50次下载
从数学和视觉上展示信号去趋势是如何影响傅里叶变换的
在计算傅里叶变换之前对信号去趋势是一种常见的做法，特别是在处理时间序列时。在这篇文章中，我将从数学和视觉上展示信号去趋势是如何影响傅里叶变换
傅里叶变换的时移特性
傅里叶变换的时移特性 傅里叶变换是一种非常重要的数学工具，可以将任何周期性信号或非周期性信号进行频域分析，从而在通信、电子工程等领域中得到广
短时傅里叶变换特点 短时傅里叶变换的意义
变化进行分析。与傅里叶变换相比，STFT可以捕捉信号在时间和频率上的局部特征，是一种非常重要的信号处理技术。 STFT的特点 1. 局部性：
傅里叶变换公式理解
傅里叶变换公式理解 傅里叶变换是一种在数学、物理、工程和其他科学领域中常用的工具，它是一种将一个函数从时域转换到频域的方法。傅里叶变换可以将一个复杂的函数表示成一个频域上各种周期函数的
傅里叶变换和离散傅里叶变换的关系
傅里叶变换和离散傅里叶变换的关系 傅里叶变换（Fourier Transform）是一种将时间域（或空间域）的信号转换为频率域（或波数域）的信号
傅里叶变换的定义 傅里叶变换的意义
连续傅里叶变换和离散傅里叶变换。最初傅里叶分析是作为热过程的解析分析的工具被提出的。 傅里叶变换的意义主要体现在以下几个方面： 1. 频谱
傅里叶变换在信号处理中的应用
在现代通信和信号处理领域，傅里叶变换（FT）扮演着核心角色。它不仅帮助我们分析信号的频率成分，还能用于滤波、压缩和信号恢复等多种任务。
傅里叶变换的基本性质和定理
傅里叶变换是信号处理和分析中的一项基本工具，它能够将一个信号从时间域（或空间域）转换到频率域。以下是傅里叶变换的基本性质和定理： 一、基本性
工商网监
评论