反馈控制系统的特点 如何利用反馈系统产生自激振荡？

一、引言

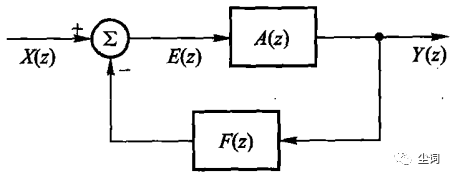
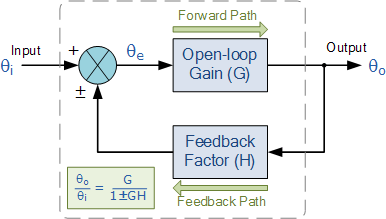
二、反馈系统的基本特性及其应用

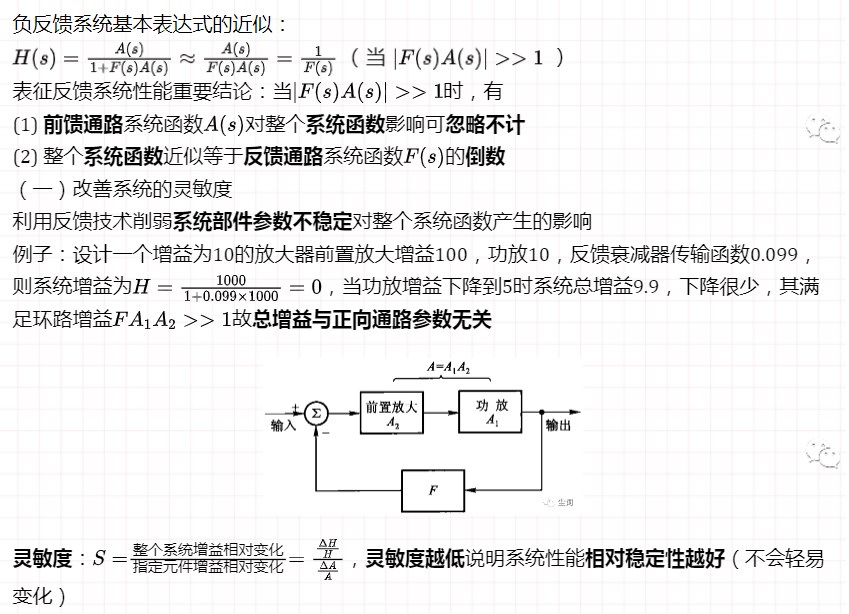
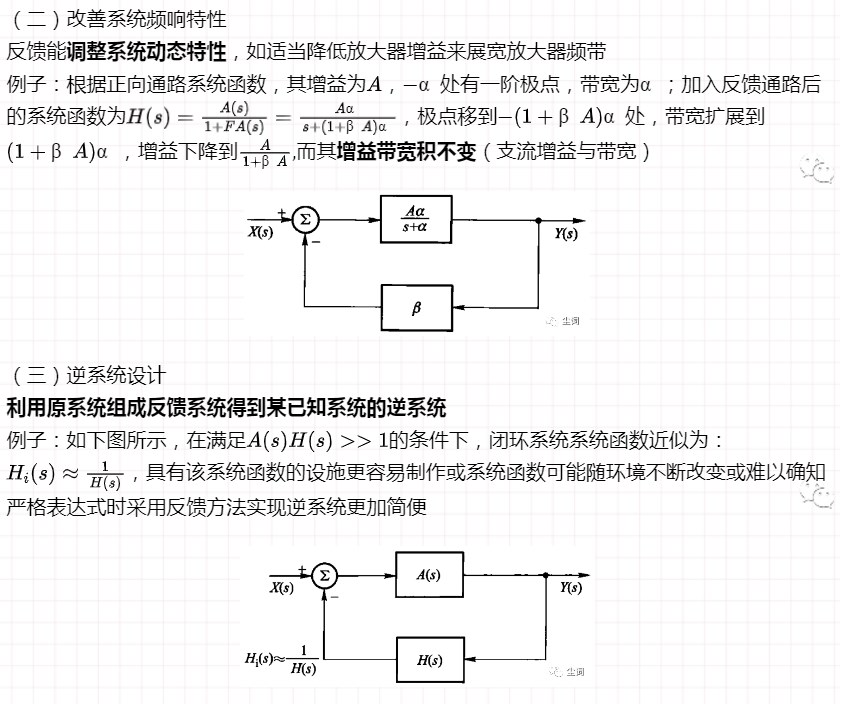
（四）使不稳定系统成为稳定系统

例如移动极点使系统变得稳定，应用如PID、火箭轨道控制和生物繁殖的节制等

三、利用反馈系统产生自激振荡

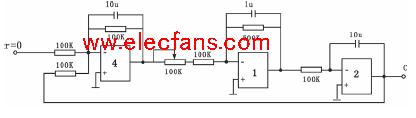
自激振荡电路反馈系统本质： 正反馈 ，工作于 临界稳定状态 ， 极点位于单位圆上 ，一般采用工作于非线性状态下的电子器件。

四、根轨迹

根轨迹法：考察闭环系统函数式中某参量变动时特征方程的极点在s平面内移动的轨迹
（一）根轨迹的模量条件和辐角条件

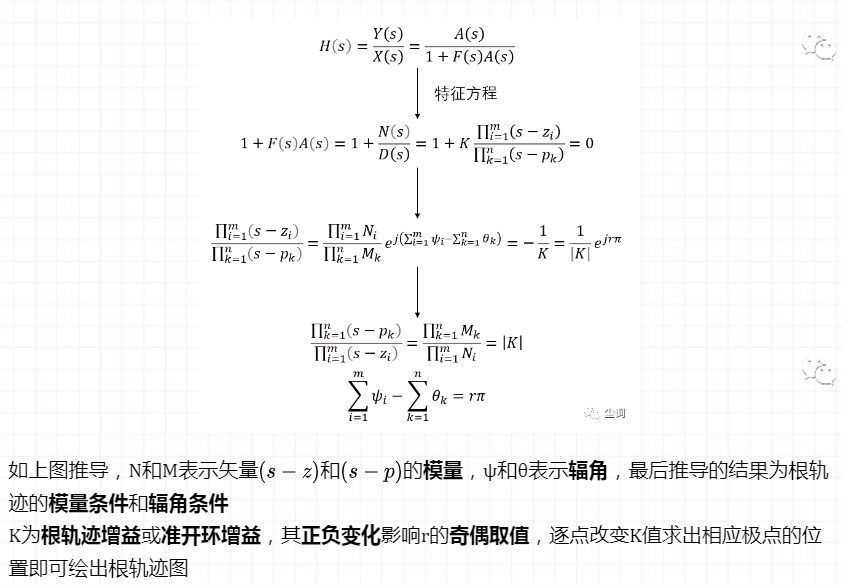
五、奈奎斯特（Nyquist）稳定性判据

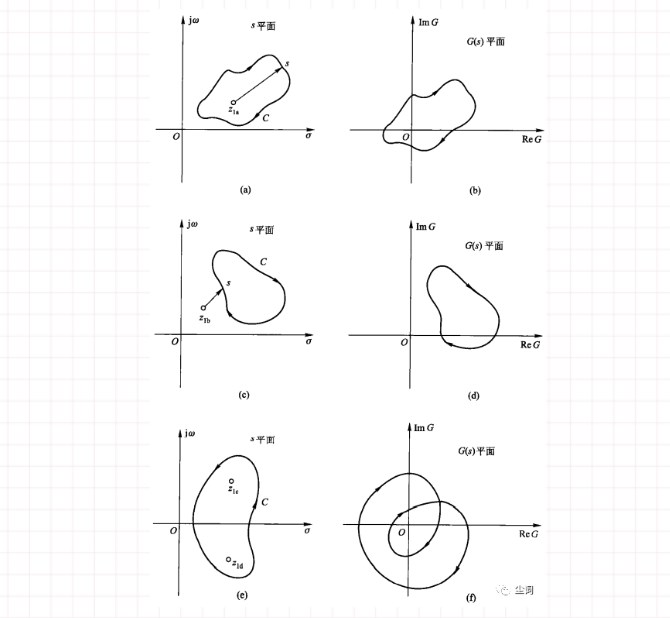
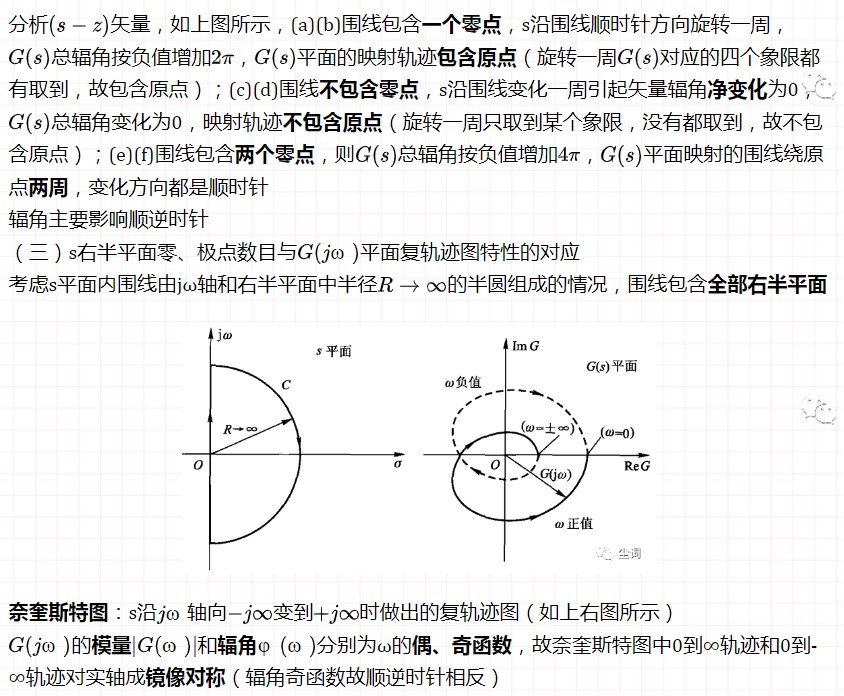
六、信号流图

七、总结

本章主要介绍反馈系统，反馈系统在各个领域都有着非常大的作用。反馈系统主要分为前向通路和反向通路两部分。灵敏度是系统的一大指标，灵敏度越低说明系统性能相对稳定性越好。通过反馈的方式可以很好地调整系统的 稳定性 。反馈同样也能够调整系统的 动态特性 ，用反馈的方式能使 不稳定系统成为稳定系统 。

以上主要用的是 负反馈特性 ，正反馈同样也大有用处。采用正反馈使产生自激振荡。

上述采用反馈运用于系统的数学原理， 本质都是利用系统函数极点在s左半平面系统稳定、在s右半平面系统不稳定的性质 。不稳定系统加上负反馈变成稳定，从系统函数来看本质就是使系统函数没有右半平面的极点；自激振荡采用正反馈则是使极点位于s平面虚轴上（离散就是单位圆上），这样使系统工作与临界稳定状态，就能产生振荡。

介绍的根轨迹判定和奈奎斯特稳定性判据能够判断系统稳定性，奈奎斯特更进一步无需求出极点精确位置，可以用实验测量数据进行分析，更加方便实用。 所有s平面的稳定性判据都是依据极点在s平面右半平面则系统不稳定来进行的 。

本章最后提出了信号流图的基本概念，能很好地简化分析。用梅森公式求解出流图输入输出间的转移函数。信号流图与梅森公式相当于 抓住了研究对象的主要矛盾，借助流图一目了然看清系统内部主体结构和关键参数 。