什么是傅里叶变换？

对于一个离开课堂十余年的射频工程师来说，傅里叶变换已经不知道埋藏在脑子里的那个角落，或者根本就没在脑子里停留过。但无论如何，傅里叶变换对现在通信的重要性还是不言而语。当我们已经习惯用频域去描述一个信号的时候，你可曾思考过其真实的样子到底是什么？为什么这几个短短的频谱就可以描述一个信号？

所以呢，我们首先得感谢傅里叶，正是傅里叶大神的天才发明，带给我们一个全新的看待问题的角度，让我们跳出时域这个圈子，站在频域的角度去看待问题。这样做又有什么好处呢？且看下文。

首先来瞻仰一下傅里叶大神的肖像，致敬两分钟。（做好阅读全文的心理准备）

其实傅里叶大神在最初提出这个思想的时候，并没有想着去解决信号的问题，而是要来描述温度的变化曲线，其实当时麦克斯韦也还没有出生。傅里叶大神在1830年去世的时候，麦克斯韦还是是个躲在妈妈肚子里的小贝比呢。发明电话的那个亚历山大贝尔还要再过十几年才出生。所以，无心插柳柳成荫吧。其实傅里叶变换除了在通信上有很重要的应用，在很多领域都有着不可替代的重要性。其作为一个数学工具，已经遍布现代科技的各个角落。傅里叶大神当时在法国科学学会上发表了一篇论文，这篇论文用正弦波来描述温度变化曲线。如果只简单描述温度曲线的话也就罢啦，他出人意料的提出了一个在当时具有相当大的争议性的论断：任何连续周期信号可以由一组适当的正弦曲线组合而成。就像我们做选择题一样，太武断的答案一定是错的，所以当时人们也特别质疑过这个论断，最著名的当属两个最著名的数学家拉格朗日和拉普拉斯。当时他们哥俩是傅里叶这篇论文的审稿人。所以说当时真是个神仙打架的时代。刚好在傅里叶大神的这篇论文审查时，拉格朗日和拉普拉斯两位拉氏牛人就干起来了。拉普拉斯同意傅里叶的观点，并同意发表这篇论文，而拉格朗日则坚决反对，因为拉格朗日坚决认为，傅里叶的方法无法表示带棱角的信号。大家被高等数学里面拉格朗日的各种数学分析方法折磨，就知道，这个牛人我们惹不起，当时更没人去挑战拉格朗日的权威。因此这个论文就迟迟没有发表。直到拉格朗日去世15年之后才公布于世。

不用说，现在傅里叶的论断确实是正确的，为什么呢？因为老师说了，我们学了。那到底是不是这个回事呢？

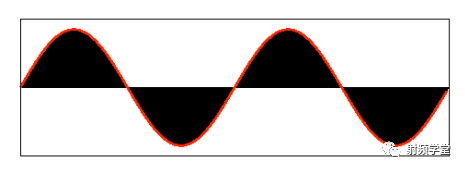
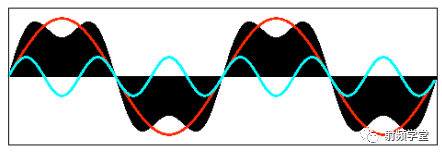
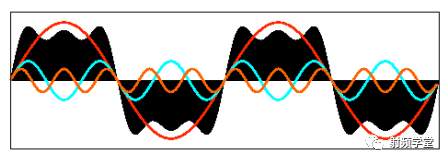
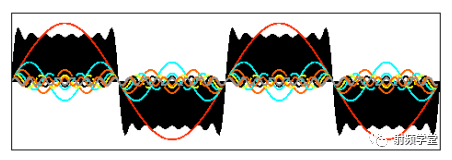
我们先来看一下矩形信号能不能用一组适当的正弦曲线来组合而成？看下图所示，一个正弦曲线时，和矩形差远了。但是当叠加的正弦信号越来越多的时候，这个组合而来的图形就越来越方了。当有无穷多个正弦曲线组合到一起的时候，这个组合图就是矩形了。奇怪的是拉格朗日发明了无穷级数，怎么能没想到这点呢？可能是屁股决定了脑袋。

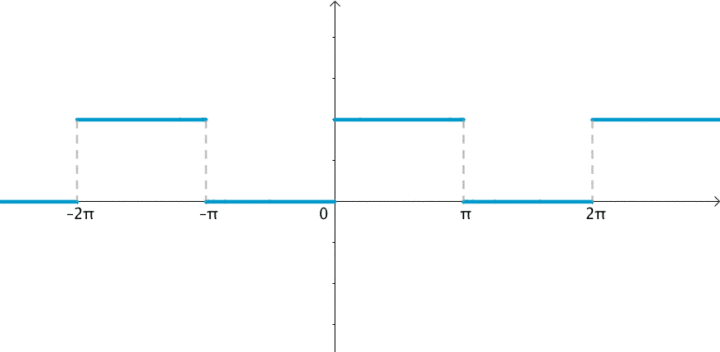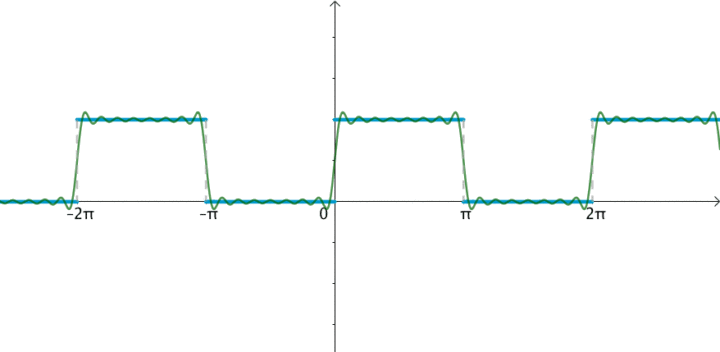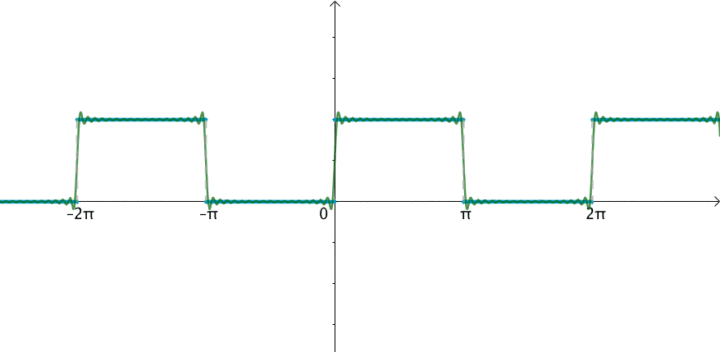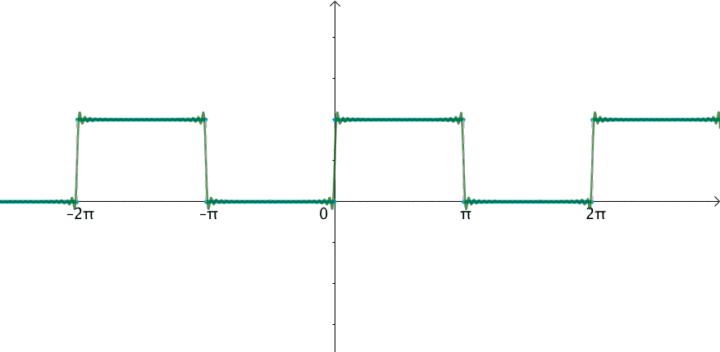
当然，人们对傅里叶的论断又做了补充和扩展。傅里叶变换就是：

f(t)是t的周期函数，如果t满足狄里赫莱条件：在一个以2T为周期内f(X)连续或只有有限个第一类间断点，附f（x）单调或可划分成有限个单调区间，则F（x）以2T为周期的傅里叶级数收敛，和函数S（x）也是以2T为周期的周期函数，且在这些间断点上，函数是有限值；在一个周期内具有有限个极值点；绝对可积。

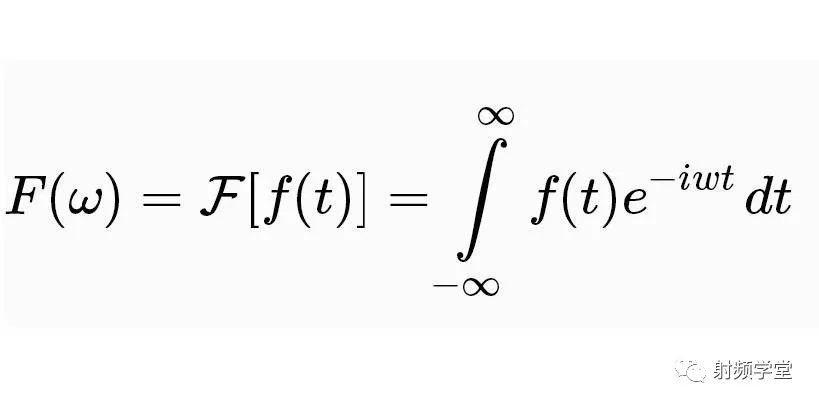
我们先把上面这个公式抛在脑后，接着讲一下为什么是正弦曲线Sin（x）/余弦曲线？因为它简单啊。它就是一个棍在转圈圈。当一个点在绕着一个圆心做圆周运动时，其随时间变化的曲线就是正弦曲线/余弦曲线。

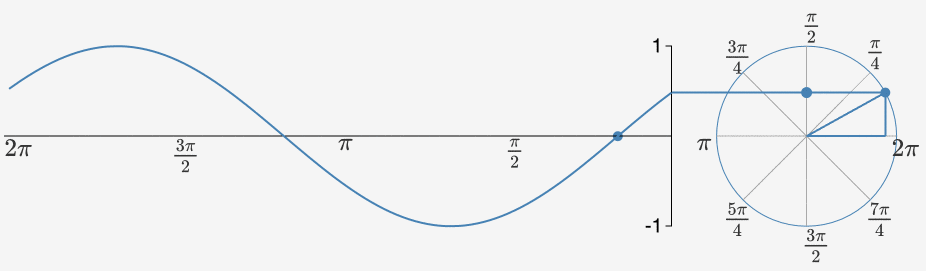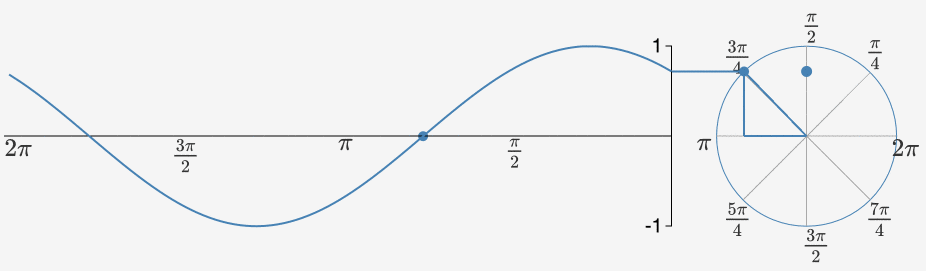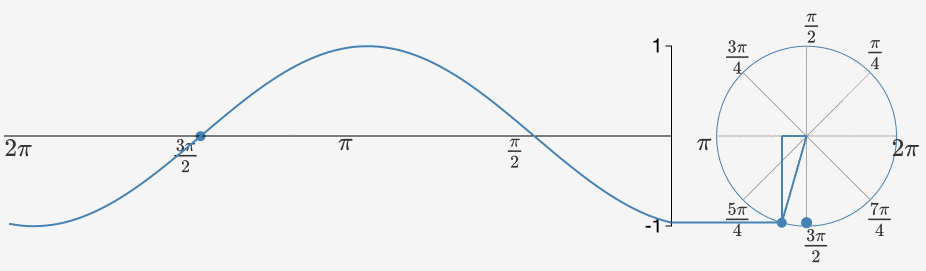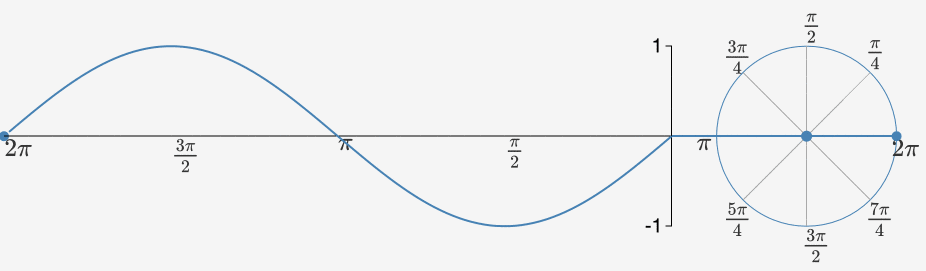
当我们把一组沿着不同圆周，不同圆心转圈圈的点都拉到时间轴上来的时候，其就会变得越来越方。

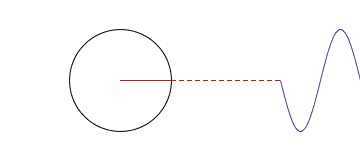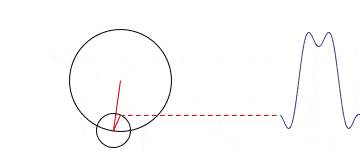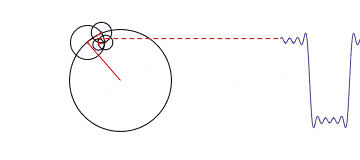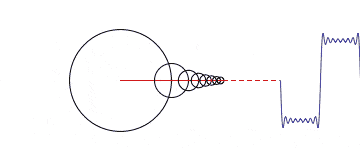
那跟频域有什么关系呢？

好像有没啥关系，这就是傅里叶级数吧。

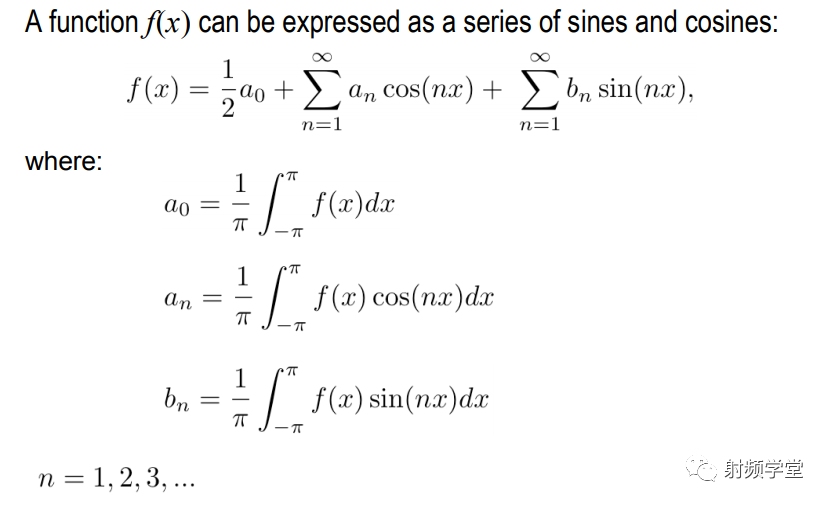
没错，就是傅里叶级数，但是把傅里叶级数的求和表示成积分形式就是傅里叶变换。

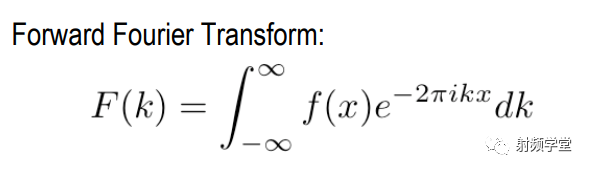
可能这里大家有点疑惑，上面傅里叶级数用的是三角函数Sin和Cos，但是下面的傅里叶变换却换成了e的指数。原因有两个，一是，太懒了，不想再编辑公式，第二个是感谢欧拉！欧拉统一了e的指数和正余弦函数：

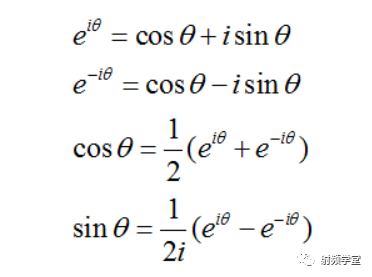
我们继续研究上文的那个矩形曲线。我们把组成矩形曲线的这些正弦曲线铺开放平，就可以观察到它的频域方向。从频域方向看过去，就是一个个一定幅度的固定在某一频率上的线。从频域方向看过去，所有都静止了，没有时间了。也就是说，我们通过傅里叶变化，把信号从时域空间搬到了频域空间。

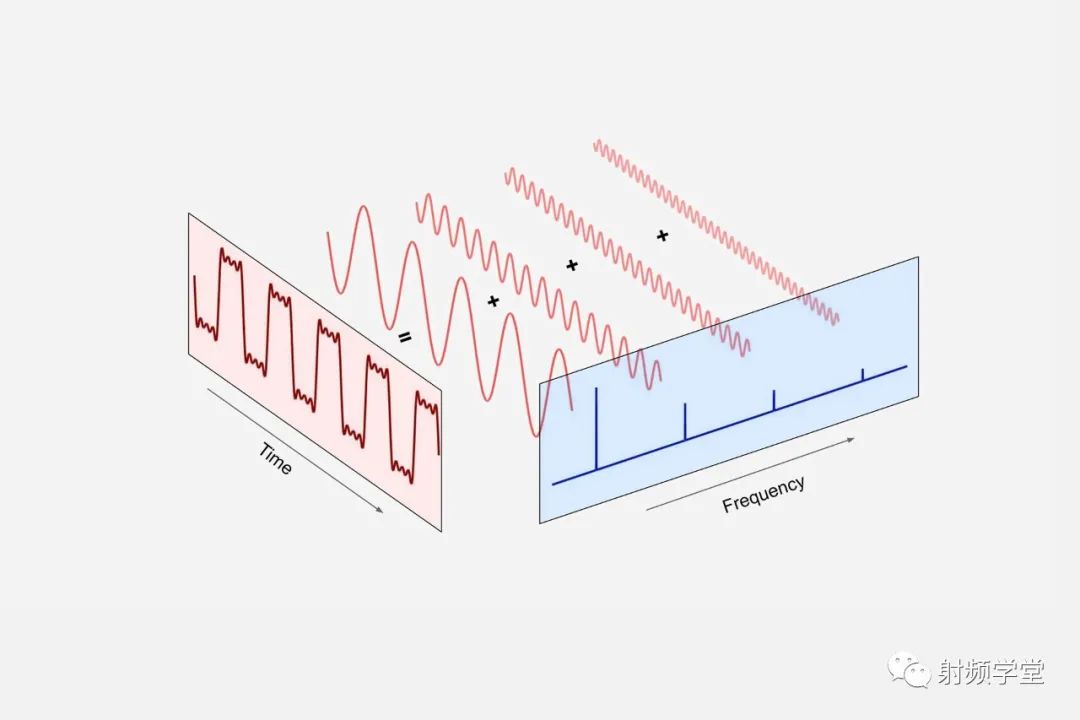
就像我们之前讨论电磁波的三要素一样，这个频域信号也具有同样的三要素：幅度，频率和相位。幅度就是信号的强弱，或者是傅里叶级数里面的an，频率就是里面的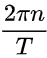，相位就是信号的初始位置。

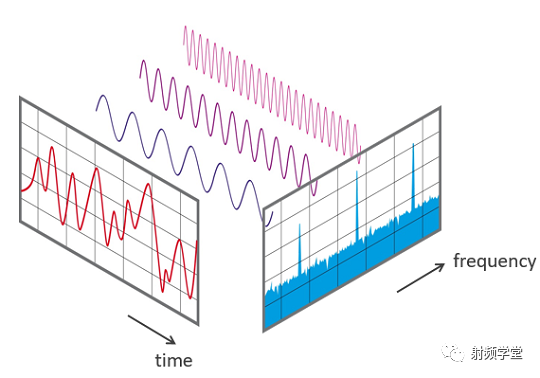
至此，我们就把信号从时域空间搬运到了频域空间，而且两个空间所描述的信号是一模一样的，就像一个人有两个名字一样，刘备和刘玄德都是指的同样一个人。频域里的信号和时域里的信号一样。所以，有时候分析一个信号，我们可以用频谱分析仪去看它的频谱，也可以用示波器去看它的波形一样。

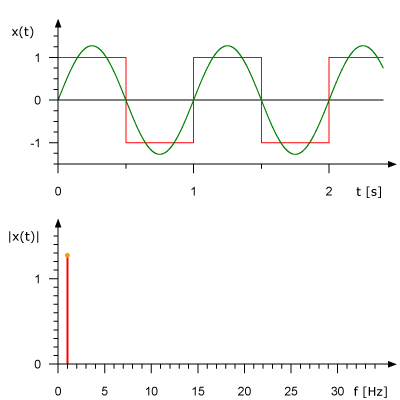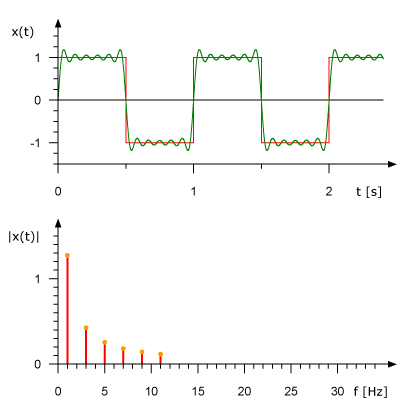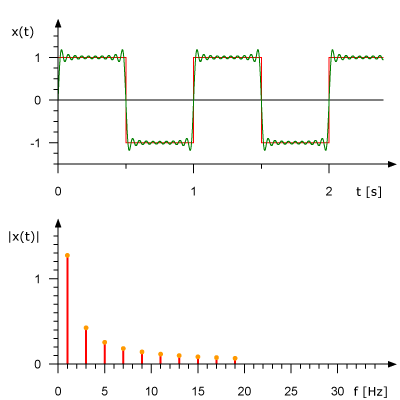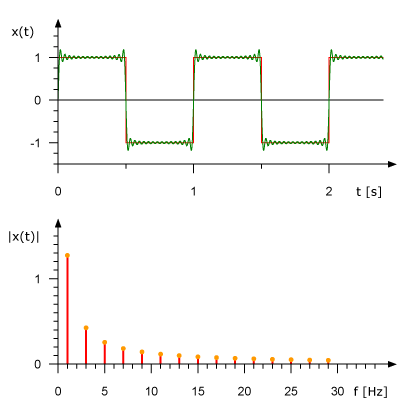
那么只要是满足狄里赫莱条件的信号，都可以用傅里叶变换把其从时域变换到频域。因为它都可以分解成一系列合适的正弦曲线的组合。

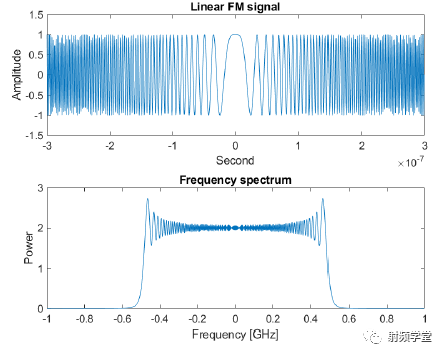
比如像FM调制的信号，其时域波形和频谱如下图所示。

审核编辑：汤梓红