P3P 问题是经典的多视图几何问题之一,其中标定的相机的绝对位姿由三个 2D-3D 对应关系决定。由于这是许多视觉系统的关键(例如定位和SfM),因此过去有很多研究关注于如何开发更快、更稳定的P3P算法。虽然当前SOTA的求解器既非常快又稳定,但仍然存在可能崩溃的配置。本文将问题代数化为寻找两个圆锥的交点。通过这个方式,我们能够分析表征多项式系统的实根,并为每个问题实例采用量身定制的解决方案。这导出了一个快速稳定的P3P求解器,它能够正确解决其它方法可能会失败的情况。实验评估表明,该方法在速度和成功率方面都优于当前的SOTA方法。
1 什么是P3P问题
PnP是指根据2D-3D对应关系集合估计相机绝对位姿,集合最小的情况是P3P问题。P3P是将2D-3D对应关系通过相机内参转换为3D-3D对应关系进行求解。给定世界坐标系中的3个3D点以及它们对应的归一化图像点,两个点集通过刚体变换关联:
其中是某个正数。P3P的目标是求解其中的旋转和平移。
2 P3P问题发展史
P3P作为一个几何问题历史悠久,比计算机视觉领域的出现都要早很久。早在1773年Lagrange就在研究这个问题,Lagrange证明该问题最多可能有4个实数解,可以转化为4次多项式问题求解。大约1个世纪后,1841年德国数学家Grunert重新研究了该问题,给出了一种直接求解方法。20世纪早期,该问题在摄影测量领域内受到关注,但主要关注点在于精调而不是从头求解。Finstenvalder和Scheufele在1937年证明P3P问题只需要找到1个三次多项式的1个根和2个二次多项式的根。该问题后来在1981年Fischler和Bolles的RANSAC论文重新露面,由于RANSAC的成功,该问题也开始受到很大的关注。
根据最后需要求解的一元多项式的阶次,P3P问题可分为两大类:求解1个四次方程和求解1个三次方程。
最近的大多数工作关注于将P3P问题转化为求解四次方程问题。Gao等人在2003年用吴零点分解法第一次给出了P3P的完成解析解。Kneip等人2011年提出了一种直接由计算相机绝对位置和旋转的方式求解P3P问题的方法,避免了特征值分解或奇异值分解。Ke等人2017年提出用相应的几何约束确定相机的旋转。Banno和Nakano分别于2018和2019提出了P3P的直接求解法,通过估计中间坐标系中的距离,使得旋转矩阵可以形式化为距离的线性表示。
与基于四次方程的方法不同,基于三次方程的方法在P3P问题的文献中没有得到太多关注。自Finstenvalder和Scheufele在1937年的工作以来,Grafarend等人在1989年也使用了三次方程,他们试图将(3)简化为齐次形式,然后使用与Finstenvalder和Scheufele相同的技术求解。Haralick等人在1991年回顾了P3P问题的主要基于三次方程的解法,并讨论了数值精度。最近,Persson和Nordberg在2018年展示了关于寻找旋转和平移的更多细节,并提出了一种使用三次方程的一个根的有效算法,该方法比以前的方法有更好的数值精度,并且更快。
3 P3P问题转化为两个圆锥曲线相交问题
参照Persson和Nordberg在2018年的解法,为了消除旋转和平移参数,如图1所示,有如下约束:
根据余弦定理,
其中。我们的目标是找到的解,从而求解旋转和平移。我们可以假设,不然3D点就和相机中心一样了。将(3)中前两个式子除以第三个式子,并通过变量替换,可以得到以下二元二次方程组:
其中
现在问题变为求两个二次方程的实数解,也就是说找到两个圆锥曲线的实数交点。
4 本文的方法
本文的方法的基本思路也是求解两个圆锥曲线的相交问题。(4)和(5)的两个二次方程可以重写为:
其中为的矩阵。为了找到交点,首先构造一个矩阵
交点可通过构建一个与真正的解相交的退化圆锥曲线找到。退化圆锥曲线由以下命题给出:
命题1(退化圆锥曲线,见《计算机视觉中的多视图几何》)如果矩阵 不满秩,则圆锥曲线退化。退化点的圆锥曲线是两条线(秩为2)或一条重复线(秩为1),可以写为:
其中。
退化圆锥曲线被构造出来后,可以被分解为(至多)两条直线(和),可以进一步很容易地与原来的两个圆锥曲线相交。
4.1 寻找退化圆锥曲线
根据定理1,退化圆锥曲线需要非满秩,即行列式为0:
得到关于的三次方程。求解(11)可以得到的值,并得到矩阵。注意原始方程组的任何解(同时属于圆锥曲线)也在退化圆锥曲线上。
对于(11)中的每个解,都可以得到一个退化圆锥曲线。根据(10),退化圆锥曲线是两条直线和的组合。那么如何将退化圆锥曲线分解为两条直线呢?
4.1.1 方法一:直接求解直线
这里展示一种寻找直线的直接方法。假定已经找到了一个退化圆锥曲线,写为如下形式:
由于,假设,矩阵也可以写为:
假定,令,则
根据(14)和(15)可以解出, 进而根据(16)和(17)可求得。在这种情况下,可以得到一对直线和。为了避免的情况,可以找到的绝对值最大的对角线元素,更稳定地计算出直线对。
4.1.2 方法二:通过求两直线相交求解直线
由于两直线参数的叉乘可得交点,可以进而从中提取出两直线。对于交点,这里展示两种求法:
(1) 零空间法:根据(10)可知, 交点在的零空间内,对于的任意零空间向量,有。我们现在必须找到,使得的尺度与(以及)一致。由于,我们有
结合(12),(13)和(18),可以推导出的范数和的元素之间的关系:
因此,可以将以正确的尺度适当地重新缩放得到交点。
(2) 伴随矩阵法:矩阵的伴随矩阵应满足:
证明:通过(13)可以得到
与相等。
给定一个矩阵,可以得到。为了避免0元素,可以找到其对角线最大的元素和对应的列,交点可以通过将该列除以对角线的平方根得到。
恢复直线:得到交点之后,根据其反对称矩阵
定义一个新的矩阵
结合(22)和(10)可得。直线对可以通过的行和列得到。
秩为1的情况:如果退化圆锥曲线包括一对重复的直线,则矩阵的秩为1。在这种情况下,可以直接从一行或一列中恢复重复的直线。
4.2 P3P问题求解
退化圆锥曲线中获得的直线过原二次方程组(7)与(8)的解(交点),因此可以通过求直线与两个圆锥曲线的交点进行求解。假设第一条直线为:
将(23)代入(5)可得一个关于的二次方程,至多有2个解。需要注意的是,我们只关心正的实数解。得到后,根据(23)可以得到。由可得。代入(3)可得关于的二次方程
由于, 可以得到的解。这种情况下,可以得到的值。由于有一对直线,的解有4种可能。知道后,可以用Gauss-Newton优化(3)的平方和对结果进行细化。之前的工作也使用了类似的细化方法。
求解旋转和平移:对于每个,首先用(1)消除平移,得到以下方程组
为了找到另一个非共面向量量对应关系,与前人工作一样,可以使用由三个3D点和图像点定义的平面的法线(见图2)。法向量也满足
其中
结合(25)和(26),可以解得旋转
得到旋转后由(1)可以求解平移。
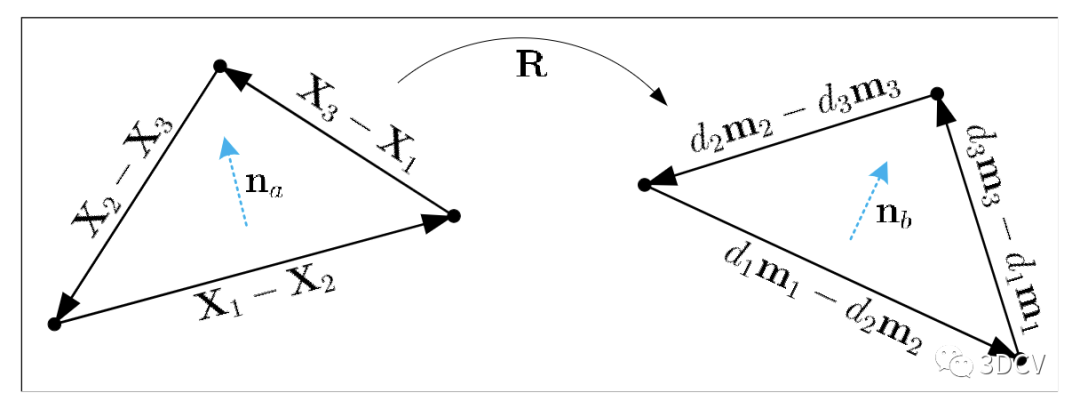
图2:从向量对应关系到旋转
4.3 可能解的配置分析以及鲁棒算法
以上展示了P3P问题求解的一个通用算法,主要包括2个步骤:
求解构建退化圆锥曲线(式(9));
将退化圆锥曲线分解为两条直线,进而代入(4)(5)的圆锥曲线求交点
接下来分析解的可能配置,并由此得到鲁棒的算法。推荐学习3D视觉工坊近期开设的课程:面向三维视觉算法的C++重要模块精讲:从零基础入门到进阶
(11)中三次方程的通解可能有四种情况:三个实根,一个实根和两个复根,一个实根和一个重根、一个实三重根。这四种可能性对应于直线和交点的不同情况。在本文的例子中,第一个圆锥曲线(4)是不定的,第二个圆锥曲线(5)是双曲线(b>0)。不失一般性,假设第一个是椭圆,并在图3中展示两个圆锥曲线的可能相对位置。简要起见,以图3b作为示例。两个圆锥曲线有四个实交点,特征三次方程有三个实根,每个实根对应于一对实直线。每对实直线在四个实交点处与两个圆锥曲线中的任何一个相交(图3b)。在其他情况下也存在类似的情况。
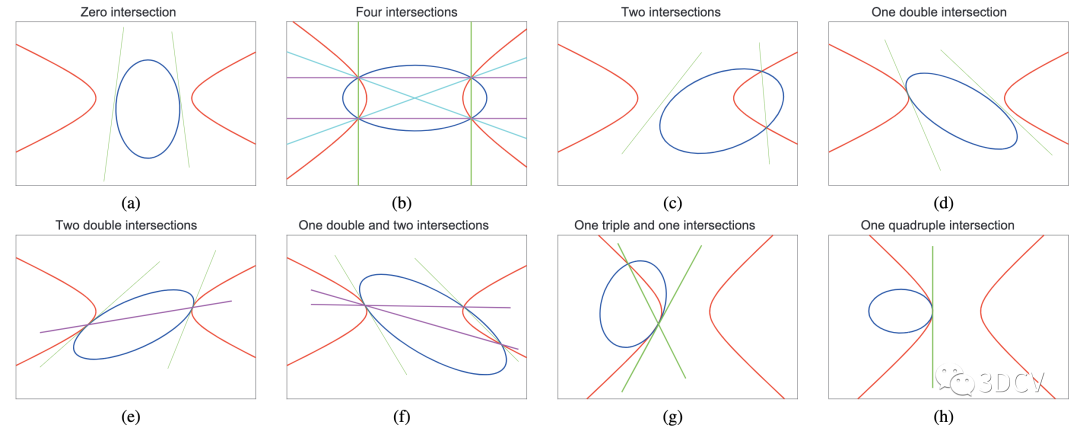
图3:双曲线和椭圆相对位置的八种可能情况的图解。具有不同颜色的一对线对应于不同的三次根。(a)-(c): 两个圆锥曲线分别具有零、四和两个实交点的一般情况。(d)-(f): 两个圆锥曲线相切的临界情况,分别有一个二重交点、两个二重交点、一个二重交点和两个交点。(g)-(h): 两个圆锥曲线彼此密切(两个圆锥在切点具有相同的曲率),分别有一个三重交点和一个四重交点
三次方程的根、线的数量和交点之间的关系如表1所示。
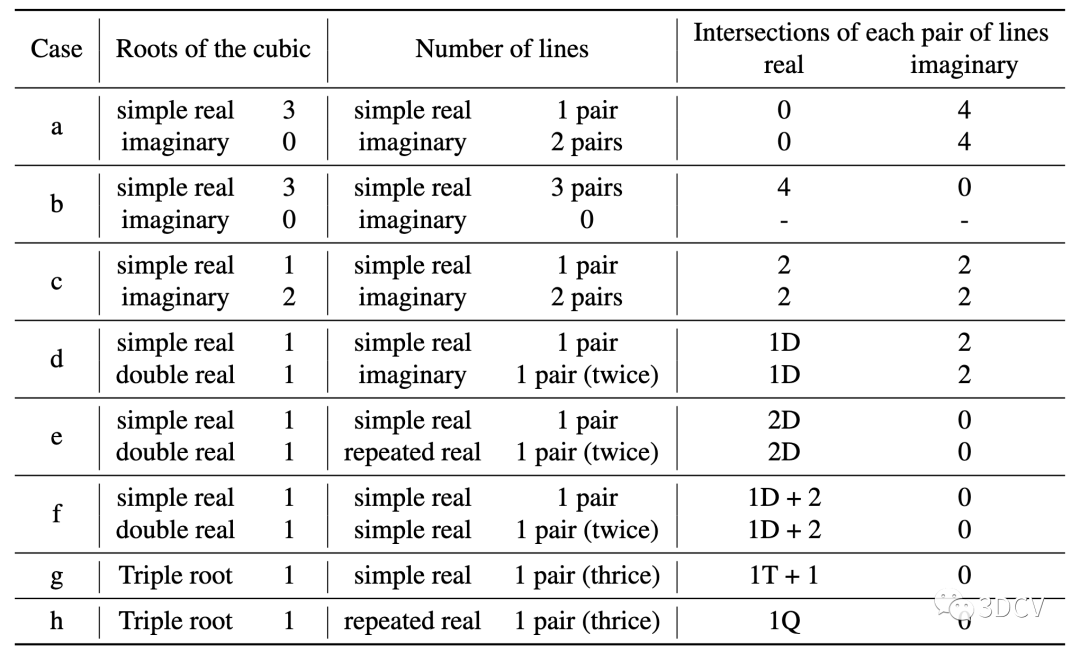
表1:三次方程的根、退化圆锥曲线的直线数和两个圆锥曲线交点之间的关系。1D、1T和1Q分别表示一个二重交点、一个三重交点和一个四重交点
假设三次方程(11)可以写成
进行变量替换可得关于的沮丧三次方程(没有二次项)
其中
(30)的判别式为:
若,(30)有三个不同的实根,其对应于情况(a)和(b)。对于情况(a),由于所有的实根都不对应于任何实交点,我们可以选择三个根中的任何一个。使用三角解找到根,该根可以对应于一对实线,也可以不对应于实线。如果选择的实根给出一对实线,可以在验证第一条直线没有实交点后跳过第二条直线。对于情况(b),三个根中的任何一个都将产生一对实线和四个实交点。
若,(30)具有一个实根和两个共轭复根,这对应于情况(c)。使用Cardano公式可以找到实根,并且可以得到一对实直线。如果其中第一条直线与圆锥曲线有实交点,则可以跳过第二条直线。否则,如果第一条直线没有实交点,就需要检查第二条直线。
若且,则(30)有一个单实根和一个重实根,这对应于情况(d)、(e)和(f)。对于情况(d),可以看到重实根在虚直线中产生。因此,对于这种情况,可以使用单实数根。
若且,则。在这种情况下,方程(30)有三重根,这对应于情况(g)和(h)。三次方的实根给出了一对实线,并且可以很容易地找到实交点。
基于以上分析和表1,可以注意到,可以使用任何一对实线来恢复实交点,并且除了情况(d)之外,三次方程的任何实根都对应于一对实直线。只需要在且时避免使用重实根。另一方面,如果,则这对直线和圆锥曲线之间一定有双重交点。为了避免重复的解,需要检查直线和圆锥曲线之间的交点。整个过程如算法1所示。推荐学习3D视觉工坊三维点云课程:三维点云处理:算法与实战汇总

5 实验
5.1 消融实验
本文提取直线的几种方法对比
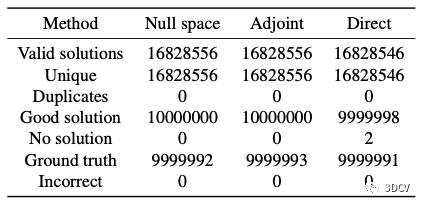
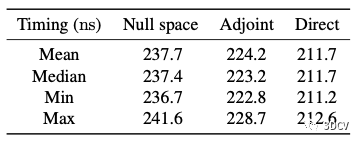
直接法速度最快,但伴随矩阵法最稳定。实践中推荐用伴随矩阵法。
5.2 与SOTA方法对比
5.2.1 数值稳定性
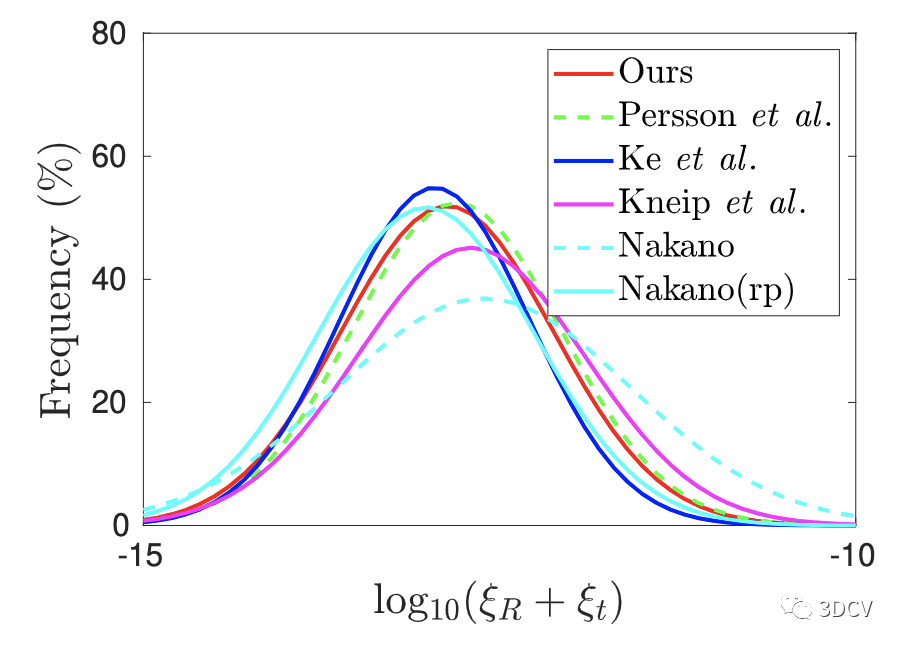
图4:高斯核平滑直方图,在无噪声数据上运行 100,000 次运行的旋转和平移误差之和。测量估计和GT之间误差的 L1 范数。
可以看到所有方法的都是数值稳定的。Nakano(rp)表示带root polishing(利用Gauss-Newton方法优化根),该方法更多的分布在小误差范围。
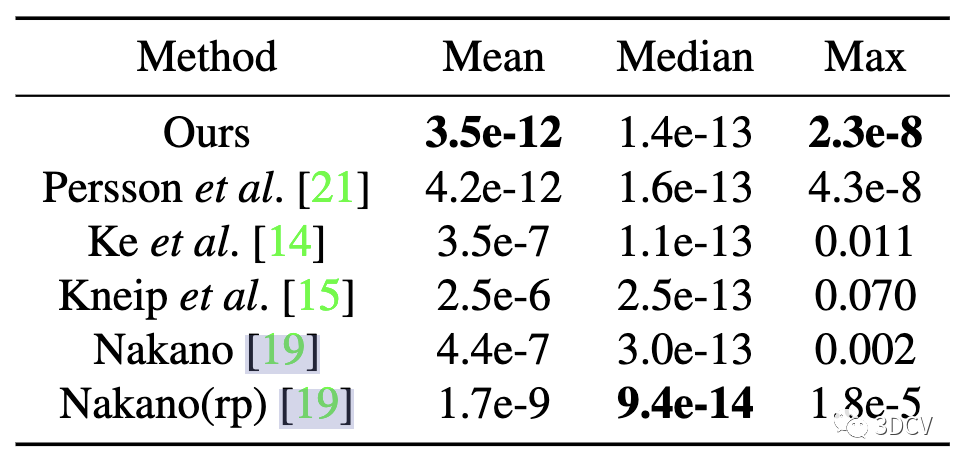
表2:误差的平均值、中位数和最大值。粗体表示最好的结果
本文提出的求解器在均值误差和最大误差上的性能最好,而Nakano(rp)求解器在中值误差上的性能最好。请注意,基于四次的求解器包含的失败案例,在此实验中是删除了的。
5.2.2 解的对比
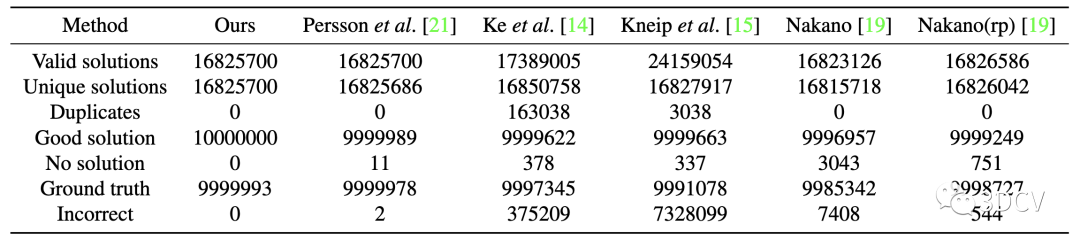
表3:与SOTA求解器对比
本文的求解器优于现有的方法。对于几乎所有的试验,都能找到好的解和GT,没有重复或错误的解。基于四次方程的Ke等人和Kneip等人的方法有很多重复解和错误解。因为他们用了四次方程的所有4个根(忽略虚部)来找到可能的估计,提高找到GT的可能性是可以的,但会损失其效率,因为实践中每个假设需要用RANSAC进行评估。Nakano求解器用的虚部阈值过滤不必要的复根,但结果没有本文的方法好。Ke等人与Kneip等人的方法也能够用类似的阈值过滤四次方程的根,从而减少重复和错误解。
5.2.3 运行时间对比

表4:平均运行时间对比,次尝试,每个尝试100次
基于三次方程的求解器比基于四次方程的要更高效,所提出的求解器比SOTA方法快15.4%,加速主要原因有两个:
基于相对位置和判别式的分析,可以快速选择三次方程的稳定根,根据判别式的符号可以避免没必要的计算。
从退化圆锥曲线中恢复直线的方法比Persson等人的方法更高效。本文用C++复现的Nakano方法比原始的MATLAB实现慢,可能是用了不同的矩阵计算库导致的。
5.3 失败案例分析
Persson等人的方法在没有解的情况下,其判别式非常接近于0。这是因为判别式为0对应于图3中的(d)-(h)这些临界情况,由于浮点数的舍入误差和数值不稳定性,这些情况下很难恢复运动参数。本文发现大多数失败案例是(d)和(f)的情形,(e)(g)(h)很少发生。
与危险圆柱的关系
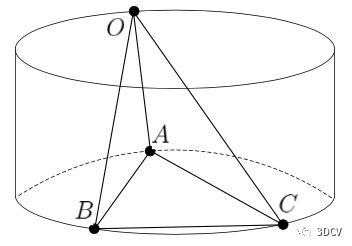
图5:危险圆柱是指三个3D点A,B,C为圆形环绕点的圆柱,其轴垂直于ABC平面
之前有工作指出,如果光心位于危险圆柱的表面,则P3P问题的解不稳定。本文发现危险圆柱会导致判别式,即对应于图3中的临界情形。
5 总结
本文重新审视了 P3P 问题,特别是研究了基于两个圆锥曲线相交的解法,类似于 Persson 和 Nordberg的方法。通过分析可能的解的集合并明确枚举极端情况,能够设计一个快速稳定的 P3P 算法。实验表明,与以前的方法相比,本文的求解器更鲁棒且更快。
局限性
本文的方法基于研究两个圆锥曲线的实交点。然而,P3P 问题是特殊的,因为解应该是正实数。三次方程可能有更多的约束,不幸的是,本文没有发现一个很好的方法来做到这一点。请注意,式(4) 和 (5) 可以用同伦延拓来求解,该方法擅长解决大规模平方系统。但对于 P3P 问题,本文发现它不如当前基本上闭式的求解器有效。
-
相机
+关注
关注
4文章
1383浏览量
54120 -
P3P
+关注
关注
0文章
2浏览量
6648 -
求解器
+关注
关注
0文章
78浏览量
4590
原文标题:CVPR2023 | 如何设计一个更快更鲁棒的P3P求解器?
文章出处:【微信号:3D视觉工坊,微信公众号:3D视觉工坊】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
鲁棒模型预测控制(RMPC)是什么
偏航角对P3P位姿测量鲁棒性的影响分析
基于鲁棒性组密钥协商方案设计
Linux的鲁棒性度量详解及鲁棒性关联测试分析
基于KeyStone器件特性的鲁棒性系统设计及例程解析
鲁棒优化的风储联合配置




 如何设计一个更快更鲁棒的P3P求解器?
如何设计一个更快更鲁棒的P3P求解器?











评论