在结构中开孔以符合某种工程需求是工程上常见的现象,例如机械结构中连接件、以及隧洞开挖、水利工程中的泄洪口等,而确定孔边应力分布,进而对开孔构件进行强度校核,包括刚度校核、稳定性判定是确保各类开孔工程安全的基础。针对于这一问题,巴黎综合理工学院的两位校友拉梅(Gabriel Lame, 1795-1870)和克拉贝隆(Emile Clapeyron,1799-1864)于1831年率先得到了薄壁圆筒同时受内压和外压的解,这为结构开孔问题做出了奠基性工作。
设有一薄壁圆筒,受内压为qa,受外压为qb,圆筒的内半径为a,外半径为b,如图2所示。在这一问题中,圆环为轴对称,同时载荷也为轴对称,该问题为(平面)轴对称问题,其应力、应变、形变位移只是ρ的函数。
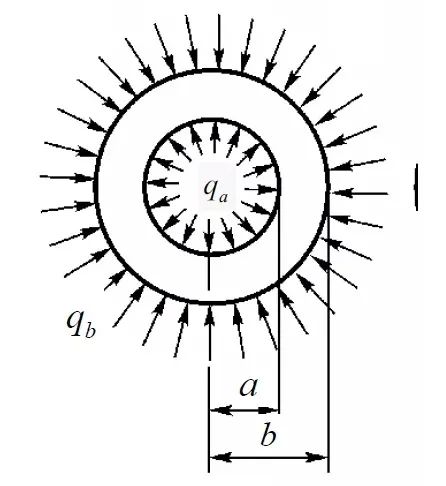
图2 受内外均匀压力的薄壁圆筒
在这种情况下,若采用极坐标系下应力函数法求解,用应力函数表达应力分量可作如下简化
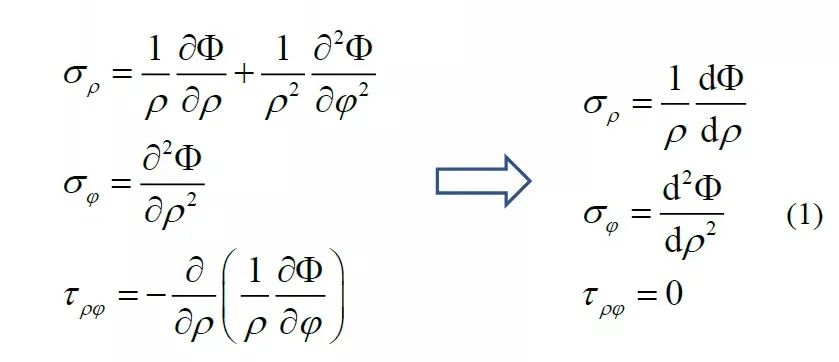
由极坐标下的相容方程推导应力函数,有
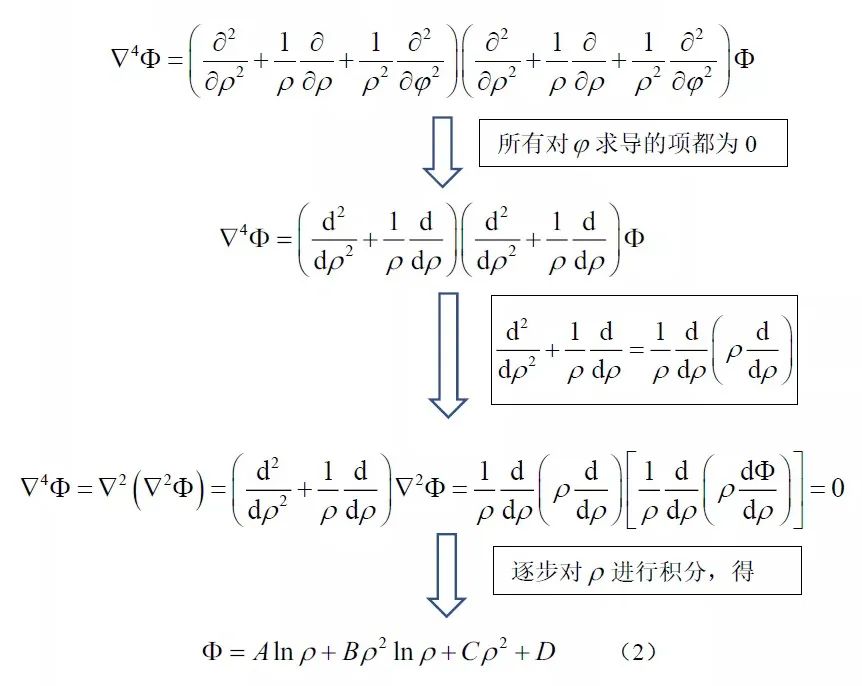
将其代入到应力函数表达应力分量的简化公式,有
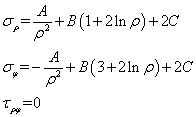
将上式代入物理方程(平面应力问题)、几何方程,可得位移解为
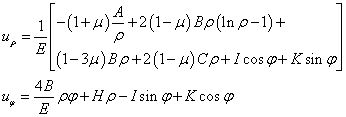
式中,含有常数H、I、K的项均为求解几何方程时增加的项,代表刚体位移,如果只考虑形变位移时,可将其视为0。此外对于上式的第2式第一项(4B/E)ρφ,筒壁任意点的坐标可表示为 (ρ, 2kπ+φ),k为整数,也就是说极坐标对一点的描述有周期性。然而,对于一点的环向位移uφ只能是一个值,这就是多连体必须要满足的位移单值条件。为了满足位移单值条件,只能有B=0。由此可见,
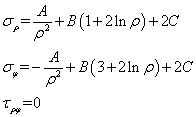
简化为
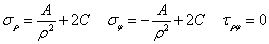
共有A和C两个常数需要确定。考虑圆筒的边界条件,在内壁上
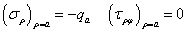
在圆筒外壁上,有
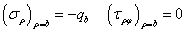
将应力分量代入,可得
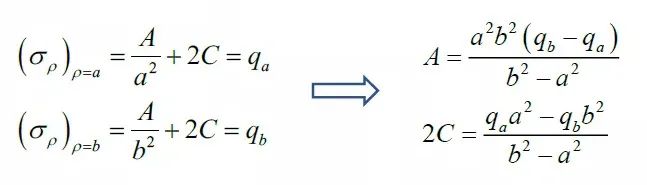
最后得,受均匀内压和外压的圆筒应力分布为
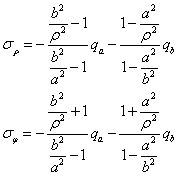
这就是拉梅-克拉贝隆解,利用该解我们可以推广得出一系列的解,例如只有内压而无外压的情况,只需令拉梅-克拉贝隆解中的qb=0;只有外压而没有内压时,只需令qa=0;若是无限大体中的圆筒只受内压,即qb=0且b>>a时,将上两式分子、分母同除以b²,并忽略1/b²,得
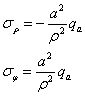
如果考虑位移边界条件,这一问题还可以推广为外壁固定有内压或内壁固定有外压,以及多层圆筒相套的接触问题,拉梅-克拉贝隆解无疑为解决结构中开圆孔问题奠定了重要的理论基础。
1898年,德国工程师吉尔斯 (Ernst Gustav Kirsch, 1841-1901) 在德国第39届工程学会一般会议上发表了他有关无限大体中含圆孔时孔口应力分布的成果。他首先回顾了拉梅-克拉贝隆解,并将其推广到无限大板开圆孔问题,但也指出了这种条件在实际工程中的有限性。从而,提出研究受载荷平板中含有圆孔的应力分布问题的必要性。
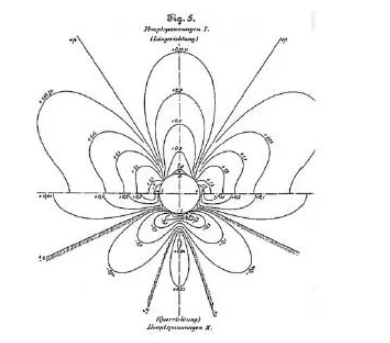
图3 吉尔斯和他的孔口应力集中
如图4所示,设有一平板,在其横向受均匀载荷q,板中心含有一半径为a的圆孔。特别注意,要求圆孔距离板的边界很远,且孔的半径远小于板的尺寸,此时就可以将其视为一无限大平板中含有小圆孔的问题。
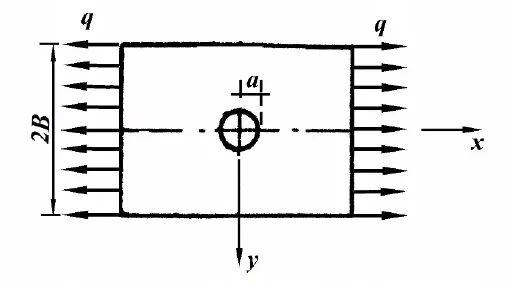
图4 受横向均匀载荷的平板含有圆孔问题
针对该问题,吉尔斯想到了绝妙的办法,通过改造边界条件,使这一问题转化为可用拉梅-克拉贝隆解的方法。当小圆孔远离边界,且圆孔远小于板尺寸时,可围绕圆孔再假定一个半径为b的圆边界,b远大于a,同时也远小于板尺寸,如图5所示。
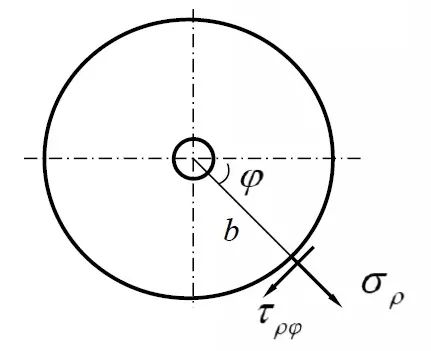
图5 围绕圆孔改造边界条件
依据图4所示的受力状态,假想边界上点的应力状态可表示为
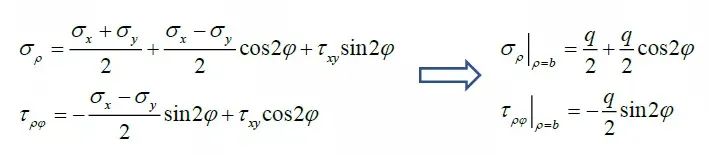
利用极坐标和直角坐标应力分量变换公式,写出假想边界上极坐标下的应力分量,有
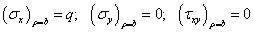
将其视为新边界上的面力,无限大方平板含有小圆孔问题,就转换成了无限大圆形板含有小圆孔问题,此时内边界条件可写为
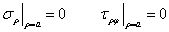
外边界条件可写为
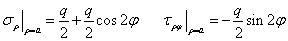
观察外边界条件,可分解为轴对称和非轴对称两个部分,我们知道当只考虑轴对称部分时,就是拉梅-克拉贝隆解,为此,吉尔斯只需要集中精力求解非对称部分,当两部分解分别得到后,叠加就可以得到最终的解。以下我们分别叙述。

问题一:考虑轴对称边界,如图5所示图形,只考虑外边界的轴对称部分,该问题可借用只有外压而没有内压的拉梅-克拉贝隆解,令受均匀内压和外压的圆筒应力分布公式中qa=0,qb=-q/2(负号表示拉应力),并考虑b>>a,有
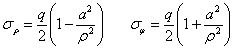
问题二:考虑非轴对称边界,观察非轴对称边界条件,再依据极坐标系下应力分量与应力函数的关系式,可假设σρ为ρ的某一函数,可设为f(ρ),乘以cos2φ;τρφ为该函数乘以sin2φ。再依据应力函数与应力分量之间的关系
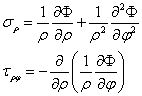
设出应力函数为
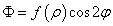
将其代入相容方程,有

在上式中,由于cos2φ不能总等于0,因此有
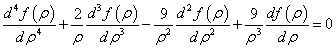
将上式两边同时乘以ρ4,上式转变为标准的欧拉方程,其求解过程如下

将f(ρ) 的表达式代回应力函数,有
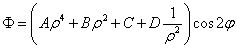
现在,我们将上述应力函数代入应力分量表达式,有
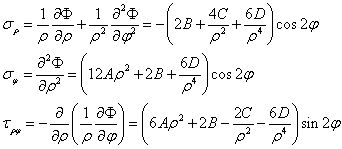
现在考虑边界条件,内边界上有
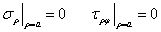
外边界上,有
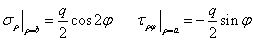
将应力分量代入边界条件,得
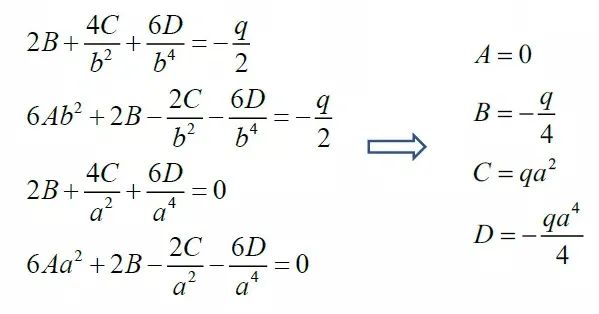
再将得到的常数代回应力分量,有
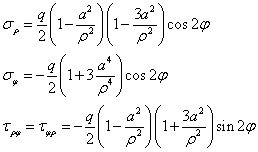
现在,我们已经得到了轴对称边界和非轴对称边界下的应力分布,主需要叠加上式和下式的结果
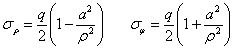
就可以得到完整的无限大平板开小圆孔的解答,如
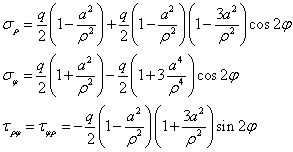
这就是无限大平板开圆孔的吉尔斯解答。由于圆孔开裂的控制应力为σφ,显然,孔边随角度变化的环向应力σφ可写为
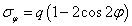
将q视为远端的均匀应力,可见,当φ=90°时,(1-2cos2φ) 取得最大值,为3。因此,圆孔周边应力最大为远端应力的3倍。当φ=0°时,环向应力为-q,这也验证了泊松效应,一个方向为受拉时,垂直方向上受压。
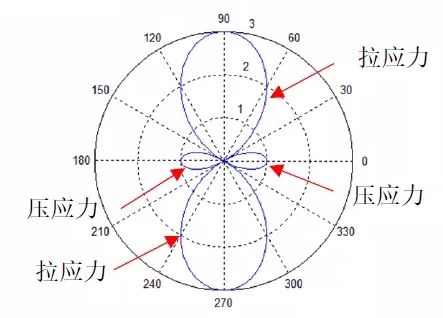
图6 孔边应力分布情况
再来观察圆孔周边应力集中的范围,先假定φ=90°,写出σφ的表达式为
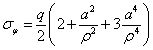
经过简单计算可以发现,当ρ=a时,σφ取最大值,为3q;当ρ=2a时,σφ=1.22q;当ρ=3a时,σφ=1.07q;当ρ=4a时,σφ=1.04q,可见在3倍半径之后,孔边应力与远端均匀应力就只有7%的差别了,并且距离圆孔越远就趋近于远端的均匀应力,如图7(a)所示。这也启示我们,当需要在结构开多个孔时,孔间的距离至少要在3倍半径之上,这样可近似认为两孔之间没有相互影响。
再假定φ=0°,写出σφ的表达式为
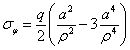
在沿着φ=0°的直线上,当ρ=a时,σφ=-q;ρ=√3a时,σφ=0,随后应力迅速变为0,如图7(b)所示。
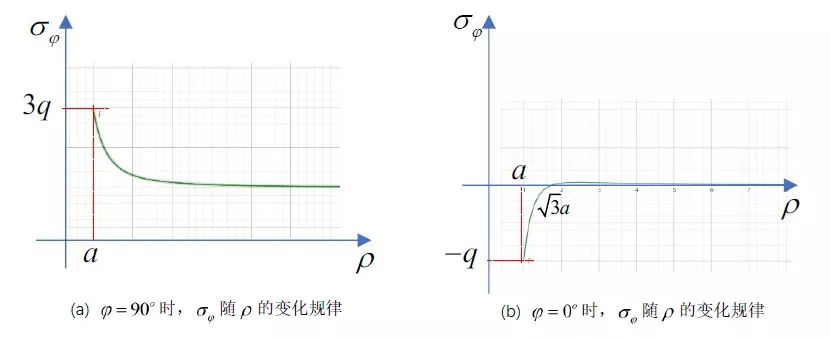
图7 环向应力随离开圆孔的距离变化时的分布
如果稍关注一下拉梅-克拉贝隆、吉尔斯的背景就会发现,他们都有矿业工程背景,他们研究这一问题的动机很可能在于解决矿业工程中地下开挖时的力分布问题。不过很快,这一问题的解利用叠加原理被推广到了多种场合下的应用。例如,双向受拉的问题分解成一个水平方向受拉和一个垂直方向受拉,两个吉尔斯解。
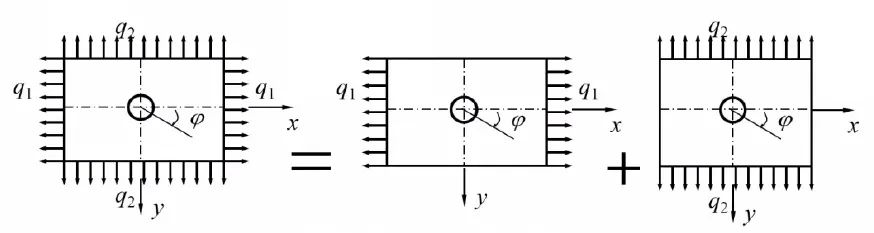
图8 双向受拉状态下的开孔问题
纯剪状态下的开孔问题,通过应力状态等效,将其等效为一个方向受拉、另一个方向受压的情况,如图9所示。
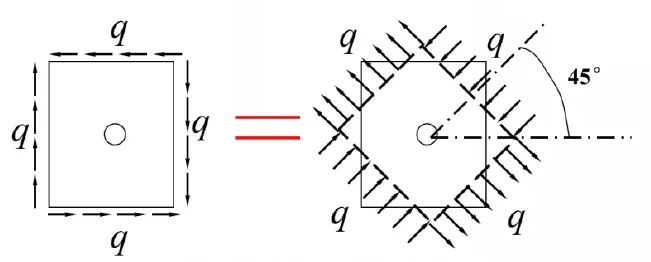
图9 纯剪状态下开孔问题
还可以通过叠加,求出当存在一群孔时结构中的应力分布。吉尔斯解的意义不仅在于为解决工程上的开孔问题提供了依据,也为另一门力学分支奠定了基础。在吉尔斯解的基础上,苏联科学家Kolosov(1909)、Inglish(1913),以及Muskhelishvili (1953) 都得到了椭圆孔的应力分布,Griffith(1921) 在Inglish 解的基础上推导了含裂纹构件的强度,奠定了断裂力学的发展基础。
编辑:黄飞
-
机械结构
+关注
关注
3文章
27浏览量
4728
原文标题:孔口应力集中问题
文章出处:【微信号:AMTBBS,微信公众号:世界先进制造技术论坛】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
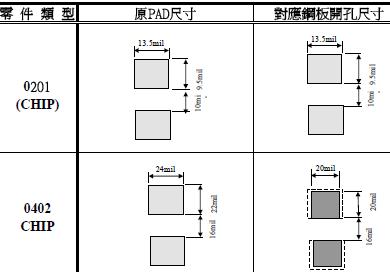
AltiumDesigner 设置焊盘在钢网上是否开孔的办法
测力传感器设计的应力集中原则
测力传感器的设计过程应力集中原则
圆孔对法兰温度场和应力场影响的有限元分析

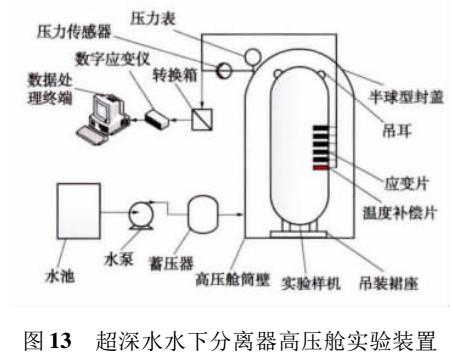
超深水水下分离器嵌入式接管马鞍形焊缝应力集中系数分布规律研究




 结构中开孔孔口应力集中问题详解
结构中开孔孔口应力集中问题详解











评论