一、交流纯电阻电路
1、电压和电流的关系
含有白炽灯、电炉、电烙铁、变阻器等负载的电路,其电感和电容可略去不计,在实用上可看作纯电阻电路。在纯电阻元件中,流过的正弦电流与电压同频率、同相位,其瞬时值等于相应电压瞬时值除以电阻,即电压和电流的瞬时值关系服从欧姆定律,最大值、有效值也遵循欧姆定律。
2、功率计算
交流纯电阻电路的功率计算如下:
电阻消耗的功率在任一瞬时都是正值,即在任一时刻都向电源吸取电能,一周期内瞬时功率的平均值称为平均功率,又称有功功率,用P表示,单位为 w,它等于电压有效值和电流有效值的乘积,即
P=UI=I2R=U2/R
二、交流纯电感电路
1、电压和电流的关系
由电感作负载所组成的电路称为纯电感电路。在纯电感电路中,自感电动势是唯一影响电流变化的因素,且线圈的外加电压和自感电动势必是大小相等、方向相反、互相平衡。由楞次定律可知,自感电动势的方向总是阻碍电流的变化,电流i较自感电动势eL超前90°,即电路的电压与电流同频率时,电流相位滞后电压相位90°。
2、感抗
计算交流电路时,常用感抗XL来表示自感电动势所产生的阻力,即电感线圈对交变电流的阻碍作用,其大小与交流电的频率和线圈本身的电感成正比,即
XL=ωL=2πfL
式中 XL--感抗,Ω;
f--频率,Hz;
L--线圈电感,H。
3、感性无功功率

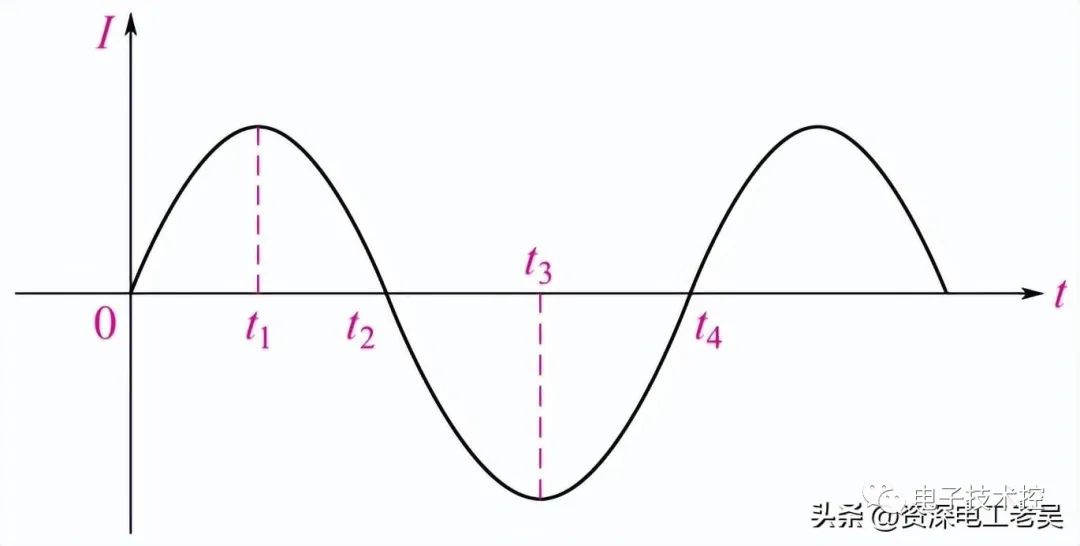
1)如上图所示功率曲线,瞬时功率以电压或电流频率的二倍关系按正弦规律变化。在0π/2 段的瞬时功率是正值,表示线圈从电源吸取能量转换为磁场能,在π/2π段的瞬时功率是负值,表示线圈将磁场能转化为电能而送还电源,以此循环往复。由此可知:电感电路中的平均功率等于零,说明该电路不消耗有功功率,只有线圈与电源之间的能量相互转换,故电感线圈是储能元件。
2)为了定量地分析电感线圈与电源之间能量交换的情况,将瞬时功率的最大值称为感性无功功率,用字母QL表示。其单位符号为var或kvar。
3)电力系统中常用无功功率来表示电源向电感性负载所提供的磁场能量的大小。“无功”决不能理解为“无用”,它是具有电感的设备正常工作的必要条件。
三、交流纯电容电路
1、电压和电流的关系
1)将电容器接在交流电源上组成的电路,并略去电路中的一切电阻和电感,叫做纯电容电路。
2)电容器是两个彼此绝缘又互相靠近的导体,是储存电能的元件。在交流电压的作用下,随着电压的不断交变,在电容元件中不断地进行充电和放电,电路中就会有持续的交流电流通过。
3)当电源电压为正值时,电容器被充电,电路中有充电电流;当电源电压下降时,电容器向电路放电,电路中有放电电流;在交流纯电容电路中,电流i与电荷的变动速率(dQ/dt)或与电容两端电压的变动速度(C·du/dt)成正比。当正弦电压是零值时,它的变动速率最大,因而此时电流具有极大值;反之,当电压是最大值时,它的变动速率等于零,因此这时电流值等于零。纯电容电路中,电容电流为
i=Cdu/dt=CUm•dsinωt/dt
=ωCUmcosωt=Imsin(ωt+π/2)
从式中明显看出在纯电容电路中, 电流在相位上超前电压π/2弧度(90°),且Im=ωCUm。
2、容抗
在纯电容电路中,电容周期性地被电源充电和对电路放电,故电容器两极上建立的电压极性与电源电压极性总是相同的,因此电容器极板上的电压相当于反电势,对交流电流具有阻碍作用,这种碍流作用称为电容容抗(简称容抗),用符号Xc表示。其电流比外施电压超前π/2相角,且同频率。
电容器的容抗Xc与交流电的频率和电容器本身的电容量C成反比,即
Xc=1/2πfC=1/ωC
式中Xc--容抗,Ω;
f--频率,Hz;
C--电容量,F。
3、容性无功功率

从上图所示的功率曲线可以看出:瞬时功率以电压或电流频率的二倍关系按正弦规律变化。充电时,从电源吸取能量并储存在电容元件的电场中;放电时,把储存在电场中的能量又送还给电源,进行着可逆的能量转换而不消耗功率,所以平均功率为零。
为了衡量电源与电容电路间能量交换的情况,将瞬时功率的最大值称为容性无功功率,用字母Qc表示,单位为var或kvar。
四、电阻与电感串联电路
1、电压和电流的关系
由于通过R、L的是同一电流,所以选电流作为参考向量,并设
i=Imsinωt
而电阻和电感上的电压则分别为
uR=UmRsinωt
uL=UmLsin(ωt+90°)
根据基尔霍夫第二定律,电路方程式为u=uR+uL
其中Ur(=IR)与I同相,UL(=IXL)超前I90°。

根据上图所示的电压三角形可求得I与U 的量值关系和相位关系。
I与U的量值关系为
U=√U2R+U2L=√(IR)2+(IXL)2
=I√R2+X2L
I与U 的相位关系为
在RL电路中,I滞后U的相位角为φ。
2、阻抗
阻抗是电路中电阻与电抗的总和,在R、L串联电路中,电路的阻抗Z为
Z=√R2+X2L,可得U=IZ或I=U/Z
阻抗Z的单位是Ω,代表 R、L串联电路对交流电流的阻力。

根据上图所示的阻抗三角形,在R、L串联电路中,如已知R与L(ωL=XL),可求出U与I的相位关系。
3、R、L电路中的功率
1)有功功率
也就是电路取用的功率,实际上是电阻所消耗的有功功率,其值为
P=URI=I2R
2)无功功率
是电路中电感与电源进行能量交换的部分,其值为
QL=ULI=I2XL
3)视在功率
电路中总电压有效值U和电流有效值I的乘积称为视在功率,用以表征电源所能输出的最大有功功率的数值。视在功率用S表示。S=UI
式中U--单位为V;
I--单位为A;
S--单位为VA(伏安),常用单位kVA。
4、功率因数

根据上图所示的功率三角形,可求得:
P=URI=UIcosφ=Scosφ
Q=ULI=UIsingφ=Ssingφ
S=√P2+Q2
cosφ=P/S,cosφ称为功率因数,φ称为功率因数角(又称阻抗角,实际上就是U与I间的相位角)。
五、电阻、电感与电容串联电路
电阻、电感与电容串联的交流电路如下图所示:

1、电压和电流的关系
由于通过 R、L、C的是同一电流,所以选电流I作参考向量。
i=Imsinωt
电阻、电感和电容上的电压分别为
uR=UmRsinωt
uL=Umsin(ωt+90°)
uc=Umsin(ωt-90°)
根据基尔霍夫第二定律,可列出 R、L、C 串联电路的方程式为
u=uR+uL+uc
用向量方程式表示时为
U=UR+UL+Uc
其中UR=IR,UL=IXL,Uc=IXc,其向量图可根据i、ux、UL、Uc方程式中的初相和各量的有效值画出,如上图(b)所示。根据向量图可求得U、I的大小与两者间的相位角:
U=√U2R+(UL-Uc)2=I√R2+(XL-Xc)2
I=U/√R2+(XL-Ⅹc)2
I与U 间的相位角为φ。
2、阻抗与电抗
阻抗Z=√R2+(ⅩL-Xc)2
式中的XL-Xc=X,称为电抗,单位为 Ω。
当XL>Xc时,电路呈感性,φ为正值,表示电流滞后电压一个φ角。
当Xc>XL时,电路呈容性,φ为负值,表示电流超前电压一个φ角。
不论XL>Xc 还是XL
3、R、L、C 串联电路中的功率
有功功率 P=URI=I2R;
电感的无功功率 QL=ULI=I2XL;
电容的无功功率Qc=UcI=I2Xc;
电路总的无功功率 Q=QL-Qc。QL>Qc时,电路呈感性;QL
视在功率 S=√P2+(QL-Qc)2
4、功率因数
电路的功率因数cosφ=P/S,当XL>Xc或QL>Qc时的功率因数称滞后的功率因数;当XL
六、R、L串联后与C并联电路
下图为R、L 串联后与C并联的电路。

1、电压和电流的关系
由于R、L支路与C支路处于同一电压之下,所以选电压的向量作为参考,即 u=UmsinωtR、L 串联电路的电流
I1=U/Z1=U/√R2+X2LC支路是电容电路,电流Ic超前电压U90°。电流 Ic=U/Xc根据基尔霍夫第一定律,i=Ic+I1。
利用以上各关系式,可作出如上图(b)的向量图。当I1sinφ1>Ic时,φ为正值,电路总电流滞后于电压一个φ角,电路呈感性状态;当I1sinφ1
2、功率
上图中R、L 支路的各项功率为P1=I21R;QL=I21XL;S1=UI1。
C支路的各项功率为Pc=0;Qc=I2cXc;Sc=UIc
所以电路各项的总功率为P=P1+Pc=P1。电路中总有功功率为各分支电路中的有功功率的算术和,即P=P1+P2+P3+...=∑Pn;
Q=QL-Qc。电路中总无功功率为各分支电路中的无功功率的代数和,感性为正,容性为负,即Q=Q1士Q2士Q3士...=∑Qn;
S=√(∑Pn)2+(∑Qn)2。电路中总视在功率为总有功功率和总无功功率的几何和。总视在功率 S≠S1+S2+...Sn,这点必需牢记。
图2(a)电路的各项总功率也可利用图1(b)直接求得:
总有功功率P=UIcosφ
总无功功率Q=UIsinφ
总视在功率S=UI
-
电容器
+关注
关注
64文章
6227浏览量
99743 -
电阻器
+关注
关注
21文章
3784浏览量
62169 -
电感器
+关注
关注
20文章
2332浏览量
70557 -
电源电压
+关注
关注
2文章
989浏览量
24000 -
交流电路
+关注
关注
0文章
184浏览量
28856
发布评论请先 登录
相关推荐




 交流电路的分析计算方法
交流电路的分析计算方法
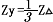











评论