傅里叶变换和系统的频域分析
傅里叶级数
由信号的分解可知,周期信号f(t)在区间(t0,t0+T)可以展开成在完备正交信号空间的无穷级数。如果完备的正交函数集是三角函数集或指数函数集,那么,周期信号所展开的无穷级数就分别称为"三角型傅里叶级数"或"指数型傅里叶级数",统称傅里叶级数。
需要指出,只有当周期信号满足狄利克雷条件时,才能展开成傅里叶级数。
狄利克雷条件:1、函数在任意区间内连续,或只有有限个第一类间断点(可去间断点和跳跃间断点)。2、在一个周期内,函数有有限个极大值或极小值。(条件的意义是使函数的傅里叶级数不仅收敛,并且收敛于f(x)。)
周期信号的分解
设有周期实信号f(t),它的周期是T,角频率Ω=2πF=2π/T,
它可分解为
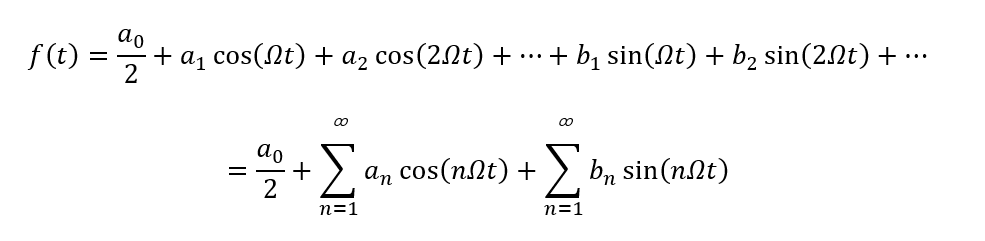
式中的系数an,bn称为傅里叶系数,它们的求法如下



式中T为函数的周期,Ω=2π/T为角频率,由上式可见,an和bn都是n(或nΩ)的函数,其中an是n(或nΩ)的偶函数,bn是(或nΩ)的奇函数,a0/2为直流分量。
通过辅助角公式将三角式合并即可得谐波式

式中

可见任意满足狄利克雷条件周期信号是由各次谐波分量组成的。
奇、偶函数的傅里叶级数
SIMPLE LIFE
注:1、奇函数乘以奇函数为偶函数;奇函数乘以偶函数为奇函数;偶函数乘以奇函数为奇函数。
2、奇函数在一个周期的积分为零;偶函数在一个周期内的积分等于其半个周期积分的两倍。
(1)f(t)为偶函数
若函数f(t)是时间t的偶函数,那么an和bn的求法便可进行化简。

(2)f(t)为奇函数
若函数f(t)是时间t的奇函数,那么an和bn的求法便可进行化简。

实际上,任意函数都可以分解为奇函数和偶函数两部分,即

(3)f(t)为奇谐函数
如果函数f(t)的前半周期波形移动T/2后,与后半周期波形相对于横轴对称,则这种函数称为半波对称函数或奇谐函数。
其傅里叶级数展开式中将只含奇次谐波分量而不含偶次谐波分量,即

傅里叶级数的指数形式
周期信号分解时,如果使用的完备正交函数集是复指数集,那么周期信号所展开的无穷级数就称为指数型傅里叶级数,即

Fn是指数型傅里叶级数的系数,它的求法为

其中Fn为复数,可表示为

-
信号
+关注
关注
11文章
2811浏览量
77185 -
频域分析
+关注
关注
0文章
20浏览量
12751 -
傅里叶变换
+关注
关注
6文章
442浏览量
42732 -
三角函数
+关注
关注
0文章
14浏览量
6779
发布评论请先 登录
相关推荐




 傅里叶变换和系统的频域分析(2)
傅里叶变换和系统的频域分析(2)










评论