直接数字合成技术(DDS)是一种频率合成技术,用于产生周期性波形。目前,从低频到上百MHz的正弦波、三角波产生,绝大多数采用的是DDS芯片完成,甚至于买来的信号源,皆是采用DDS实现。
直接数字合成技术(DDS)是一种频率合成技术,用于产生周期性波形。目前,从低频到上百MHz的正弦波、三角波产生,绝大多数采用的是DDS芯片完成,甚至于买来的信号源,皆是采用DDS实现。
为了便于大家理解,现假设DDS有一个固定的时钟MCLK——36MHz,那么每个脉冲的周期则为27.78ns。下面再为大家附上一个正弦波的“相位—幅度”表格,它具有足够细密的相位步长,比如0.01°,那么一个完整的正弦波表,就需要36000个点。
N为表格中数据点序号,phase为该点对应的正弦波相位,Am对应该相位处的正弦波计算值,介于-1 ~+1之间。Data_10为正弦波计算值转换成10位数字量的10进制表示,用一个10位DAC描述正弦波,sin(0°)应为DAC全部范围的中心,即512。sin(90°)则为最大值1023,而sin(270°)则为最小值0。
在相位从0°开始,一直到第12个点(即序号11,相位为0.11°),虽然正弦波幅度一直在增加,但始终没有增加到全幅度的1/1024,即2/1024=0.001953125,因此用DAC表达一直为512,直到第13个点(序号12,相位0.12°),正弦波计算值为0.0020944,DAC才变为513。这一段的细微变化(即前100个点)在下图1已给出。尽管管中窥豹,但可以想象,这36000个点记录了一个标准正弦波的全部。
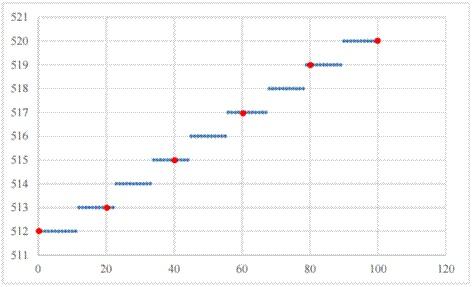
图1. DDS表中36000点正弦波的前100点
下面再将此表首尾衔接。假设相位步长为m=1,则DAC以MCLK为节拍,依序发作:第一个CLK时,DAC输出N=0时对应的DATA_OUT,即512,第2个CLK时,DAC输出N=1时对应的DATA_OUT,也是512……,可以想象,36000个CLK后,一个完整的正弦波被输出了一遍。从36001个CLK开始,又一次循环开始。如此往复,一个个正弦波接连不断被发作出来。
现在算一算,这个发作正弦波的频率是多少?显然,36000个CLK为正弦波的周期,(即1ms)其频率为1kHz。公式为:
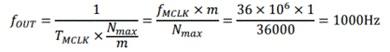
对上式参量的理解极为重要:其中,TMCLK为DDS主振时钟周期,即1/36MHz,约为27.78ns,Nmax为表格总点数,m为循环增加中的步长,如果m=1则意味着对表格一个不落的扫一遍,如果m=2,则意味着隔一个扫一遍。m越大间隔越大,扫完需要的时间越短。那么,
就代表着完成一次表格的全扫描需要的动作次数。DDS的核心思想就建立在上述公式上。改变步长m,可以改变输出频率:
① 当m=1,则输出最低频率,即:
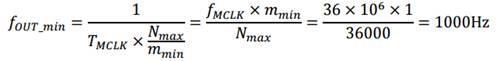
②当m每增加1,则输出频率增加
,这也是DDS能够提供的频率最小分辨:
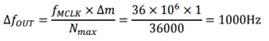
③ 当m增加到表格点数Nmax的1/1800,即20时,说明每次DAC发作,会跳过表格中的20个点,或者说一个扫完一个正弦波全表,只需要1800个点。此时,样点变化规则如图1中的红色圆点。可以算出,这样输出正弦波的频率应为:

图2是三种情况下扫出的正弦波图,分别是m=1,m=30,m=300,可以看出随着m的增大,输出频率也在同比例增加。
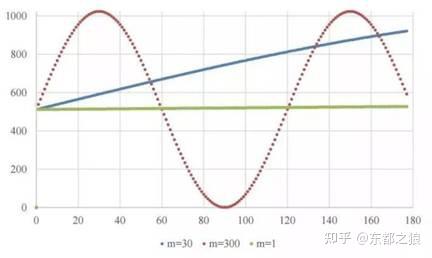
图2. 三种m获得的三种频率正弦波
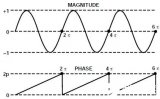
④ 当m增大到全表总数Nmax的1/4,即9000时,说明只需要4个点就可以扫完正弦波全表,此时DAC输出的正弦波,其实已经不再是正弦波,而是一个标准的三角波了,该波形只有4个相位点,分别是0°,90°,180°,270°。
⑤ 样点总数除以m不等于整数可以吗?答案是,可以。为了显示清晰,我们假设两种情况,m=40,它可以被36000除尽,为900,即每900个点可以扫描完正弦波表;m=41,不能被36000除尽,为878.0487804878……。由此得到两组数据如下表。
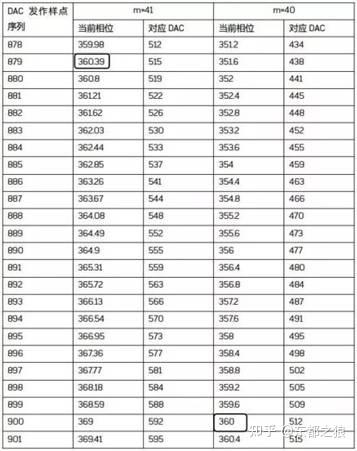
可以看出,对m=40的情况,第900点的相位为360°,即重新开始了又一个正弦波。它的周期为:
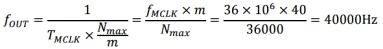
而对m=41,第878点,相位为359.98°,属于第一个周期,第879点,相位为360.39°,开始了一个新周期,但是起点不再是0°,而是0.39°。这样,它的每个正弦波,与紧邻的另一个正弦波,其相位都是不同的。但是,这丝毫不会影响总体上呈现出如下频率:
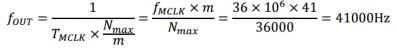
由此数据得到的波形如图3所示。你能看出41kHz正弦波,其第二个周期与第一个周期有什么不同吗?你根本看不出。
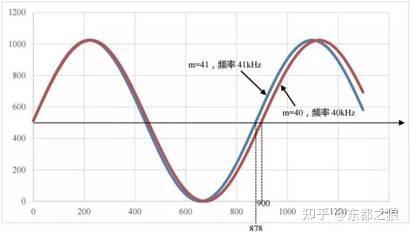
图3. m=40和41得到的正弦波
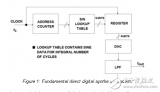
DDS内核组成
DDS技术的核心由相位累加器PA,相位幅度表和数模转换器DAC组成。以一个28位数的相位累加器为例,它可以计数0~228,或者说,它的相位表点数为228=268435456点,远比36000样点多得多,这说明实际的DDS在相位分辨上比前述举例更加细密。
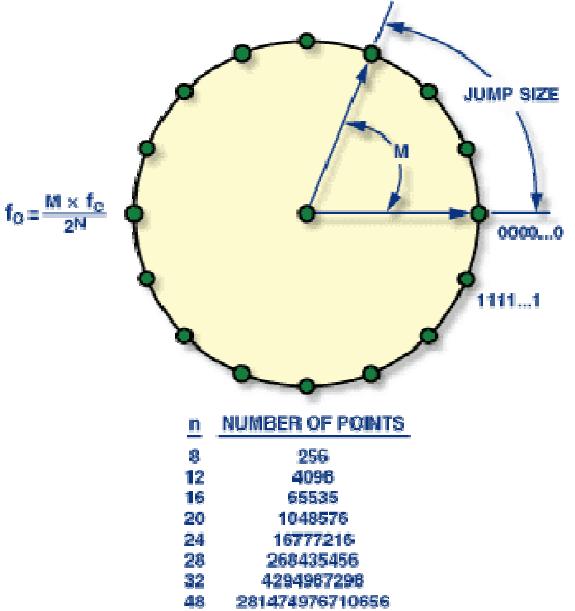
使用者需要输入一个计数步长m,当然m一定要小于228,此后外部时钟MCLK每出现一个脉冲,则PA完成一次累加。如图4所示,红色秒针以m为步长,逆时针旋转,它完成一个周期360°的旋转,需要的时间为:
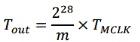
而红色秒针完成一个周期360°的旋转,正好输出一个完整周期正弦波,因此,正弦波频率为:
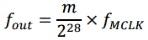
当m取1时,可以得到最低输出频率为:
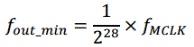
理论上,当m取227,可以得到最高输出频率为:
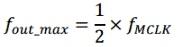
m每增加1,则会使得输出频率获得一个增量,即为最小输出频率:
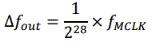
图4中,内部相位累加器具有28位,而外部相位累加器则不需要如此精细,一般仅需要14位即可。这就像你干活挣钱,每件可以挣钱1分,第一天干了272851件,折合272.851元,第二天干了291237件,折合291.237元,这可以精细计数,但到了发工资的时候,一个月累计6164.875元,可能你会得到6164.9元,就不需要如此精细了,因为这种精细是需要成本的。
图中的相位幅度表,是靠存储器实现的,存储器数量太大,自然会导致DDS芯片成本升高。而累加器,做成28位,仅仅是多几个级联的计数器而已。另外,对DDS而言,输出正弦波采用的DAC,也不需要位数过高,多数为10位,也有14位的。
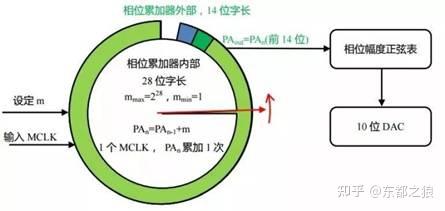
图4. DDS工作原理
为了用户使用方便,DDS内部还具有相位失调寄存器,这可以让DDS输出从某个规定相位开始。具体的DDS内核组成,还应以具体芯片为准,此处不一一赘述。
DDS技术的优势与弊端
DDS的优势在于可以发出从极低频率到极高频率范围的正弦波,且频率增量极低。以AD9834为例,它具有28位的超精细相位累加器,可承受最高75MHz的MCLK,因此,在75MHz主振情况下,它的频率最小分辨为0.279Hz,可以发出从0.279Hz到37.5MHz,频率步长为0.279Hz的正弦波。至于输出频率到底是多少,完全取决于使用者设置的m。在DDS核心技术中,可以实现如下功能:
可以精细选择输出频率,实现从低到高的频率选择。
可以快速跳频,且能够保证相位连续,这在模拟信号发生器中是难以实现的。
可以实现正交输出,可以实现相位设置。
可以实现正弦波、三角波,配合比较器可以实现同频同相方波输出。
此外,在发出高质量正弦波中,DDS技术无法实现超低失真度,是其最大的弊端。DDS技术中采用的DAC最高为14位,其积分非线性INL不可能做到很小。其次,其DAC一般均采用普通DAC,没有为降低失真度做出更多的考虑。且目前的DDS实现的正弦波输出,其失真度一般只能做到-80dB左右。
-
存储器
+关注
关注
38文章
7484浏览量
163767 -
正弦波
+关注
关注
11文章
642浏览量
55341 -
DDS
+关注
关注
21文章
633浏览量
152631 -
数模转换器
+关注
关注
14文章
1011浏览量
83166 -
相位累加器
+关注
关注
0文章
10浏览量
9184
发布评论请先 登录
相关推荐




 直接数字合成技术(DDS)是什么?DDS又是如何工作的?
直接数字合成技术(DDS)是什么?DDS又是如何工作的?











评论