探讨一下在直流充电时,充电电流是如何产生的。关键在于保持电容两端电压的连续性,不允许突变。因此,在电源接通瞬间,电容两端的电压为零,随后按指数规律逐渐上升,直至达到稳态。在稳态下,电容实际上相当于一个短路。
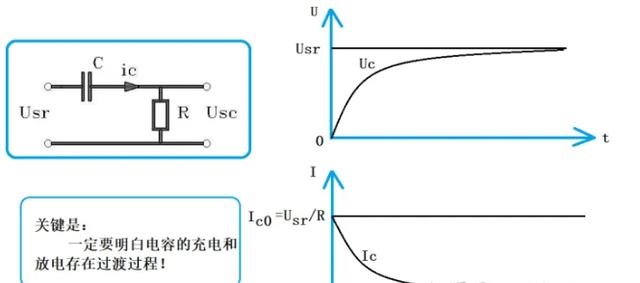
图1所示为电容充电过程的过渡阶段。当瞬间将电源电压Usr接入电容和电阻串联电路时,由于电容两端电压的连续性要求,电容被视为一个短路。因此,在时刻0,流经电容和电阻R的电流为:

随后,电容开始充电过程,电流逐渐减小。当时间达到5倍RC后,电容基本充电完毕,电流减小至接近零。此后,进入稳态。这里的RC称为时间常数。我们知道,电阻的值等于电压与电流的比值,即R=U/I。同时,电容的值等于电量Q与电压U的比值,而电量Q又等于电流I乘以时间t,即:

这就是电阻和电容的乘积等于时间的概念。电阻的单位为欧姆,电容的单位为法拉,所以时间的单位为秒。在图1中,电容充电时,其电压为:

我们可以计算出t=0、1RC、2RC、3RC、4RC和5RC时的Uc,如下所示:

可见,当t=0时,电容两端电压为零;当t=5RC时,电容两端电压几乎等于输入电压。接下来,让我们来看流经电容的电流,其表达式为:

当t=5RC时,有:

从上述推导可以明显看出,此刻的电流几乎可以视为零。必须将电容的暂态和稳态过程加以区分,只需在立刻对此进行理解,即可解决问题。下面,我们对上述讨论结果进行综合总结:1)电容充电电路经历暂态和稳态过程;2)在电容充电的初始瞬间,应特别注意电容两端电压的无突变原则,这一原则至关重要;3)通常在5RC时间之后,暂态过程基本结束;4)对于图1所示的情况,在暂态的初始时刻,电容电压Uc为零,电流Ic达到最大值,根据欧姆定律可以得出:

即电容的等效电阻等于零。此表明电容的等效电阻近似为无穷大,即此时电容等效于开路;5)对于短暂的脉冲信号输入,电容能够有效地传递信号至负载端;对于持续不变的稳定输入电压,电容只在短暂的过渡阶段中起作用,之后会隔离输入信号;对于交流信号,其情况介于前述两种情形之间。交流信号频率越高,通过电容的可能性越大。
这个特性被称为高通滤波器功能。虽然交流信号能够通过电容,但会经历一定的幅度减弱。这表明在稳态情况下,电容能有效地隔离直流,并呈现高通滤波特性。总结而言,对于任何包含电容和电感的电路,务必分别从暂态和稳态角度进行分析,以获得准确结论。
-
电容器
+关注
关注
64文章
6205浏览量
99326 -
电感器
+关注
关注
20文章
2324浏览量
70415 -
电源电压
+关注
关注
2文章
986浏览量
23946 -
电容充电
+关注
关注
0文章
68浏览量
8576 -
高通滤波器
+关注
关注
0文章
97浏览量
11009
发布评论请先 登录
相关推荐




 直流给电容充电时充电电流是如何产生的?
直流给电容充电时充电电流是如何产生的?











评论