串联和并联电阻器
电阻器可以单独串联连接,也可以单独并联连接。一些电阻电路由串联和并联网络的组合组成,以开发更复杂的电路。这些电路通常称为混合电阻电路。即使这些电路组合了串联和并联电路,计算等效电阻的方法也没有变化。
单个网络的基本规则,如“相同的电流流过串联电阻器”和“并联电阻器两端的电压相同”适用于混合电路。
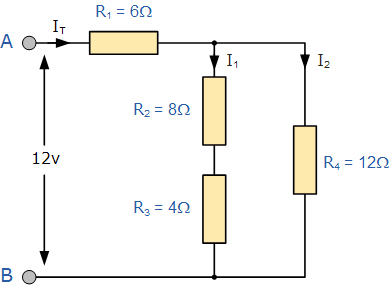
混合电阻电路示例如下所示
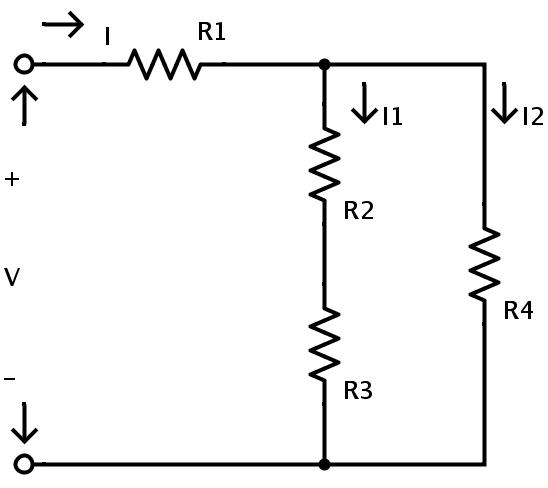
它由混合电阻电路组合中的四个电阻R1、R2、R3和R4组成。电源电压为V,电路中流动的总电流为I。流过电阻R2和R3的电流为I1,流过电阻R4的电流为I2。
这里的电阻R2和R3串联组合。因此,应用串联电阻规则,R2和R3的等效电阻为:
RA=R2+R3
这里RA是R2和R3的等效电阻
现在,电阻R2和R3可以用单个电阻RA代替。所得电路如下所示。
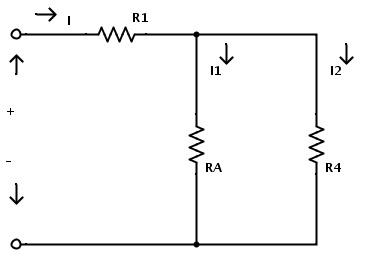
现在电阻RA和R4是并联组合的。因此,通过应用并联组合电阻规则,RA和R4的等效电阻为
RB=RA×R4/(RA+R4)
这里RB是RA和R4的等效电阻
现在我们可以用单个电阻RB代替电阻RA和R4。更换电阻后,产生的电路如下所示。
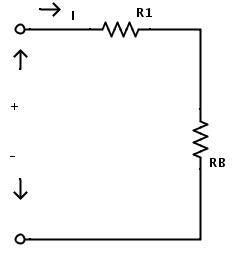
现在电路仅由两个电阻组成。这里电阻R1和RB也是串联组合的。因此,通过应用串联电阻规则,总电路等效电阻为
REQ=R1+RB
这里REQ是总电路等效电阻。现在电阻R1和RB可由单个电阻器代替REQ
上述复数电路的最终等效电路如下所示。
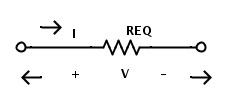
虽然它们看起来很复杂,但通过遵循串联电阻和并联电阻的简单规则,混合电阻电路可以简化为仅由一个电压源和一个电阻组成的简单电路。
串联和并联电阻器示例
让我们计算以下电路的等效电阻,该电路由7个电阻组成:R1=4Ω、R2=4Ω、R3=8Ω、R4=10Ω、R5=4Ω、R6=2Ω和R7=2Ω。电源电压为5V。
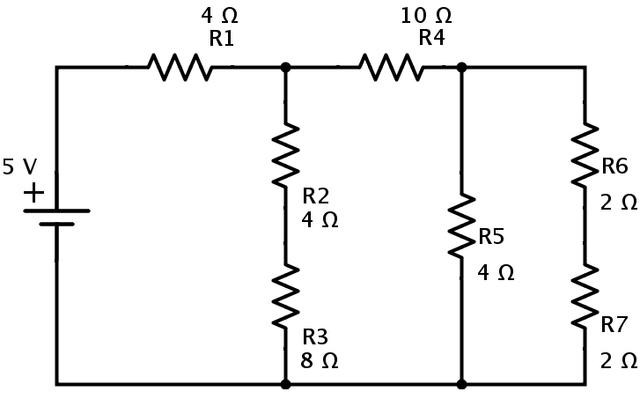
现在电阻R6和R7串联组合。如果R6和R7in系列的等效电阻为Ra,则
Ra=R6+R7=2+2=4Ω
由此产生的电路简化为如下所示的电路。
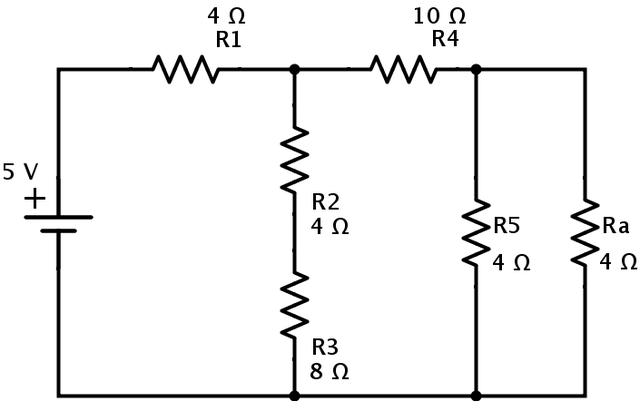
在上述电路中,电阻Ra和R5是并联组合的。因此,Ra和R5的等效电阻为
Rb=(Ra×R5)/(Ra+R5)=(4×4)/(4+4)=2Ω.
然后简化电路如下所示。
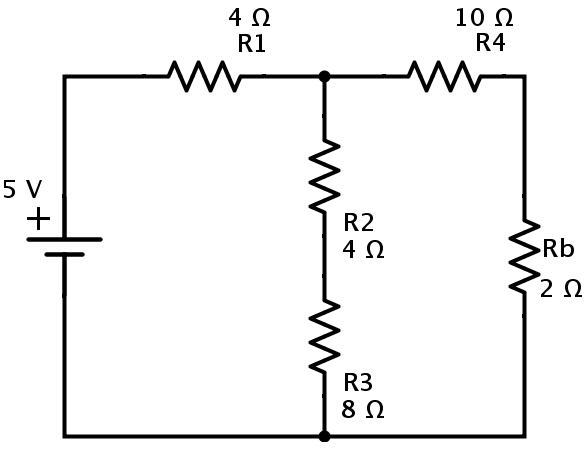
在该电路中,电阻R4和Rb是串联组合。
Rc=R4+Rb=10+2=12Ω.
现在我们可以更换电阻R4和R。b电阻Rc如下所示。
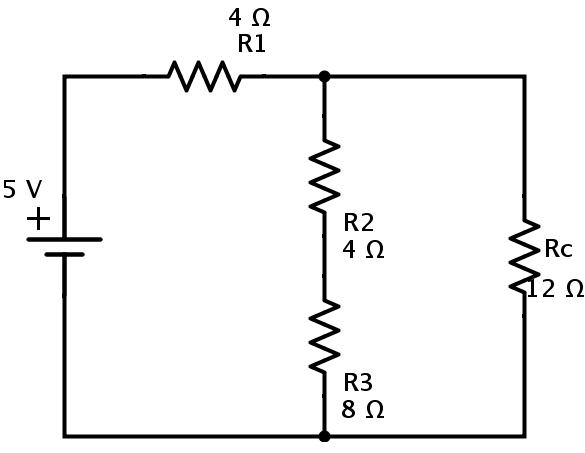
在上述电路中,电阻R2和R3再次串联组合。如果Rd是R2和R3的等效电阻,则
Rd=R2+R3=4+8=12Ω。
等效电路为
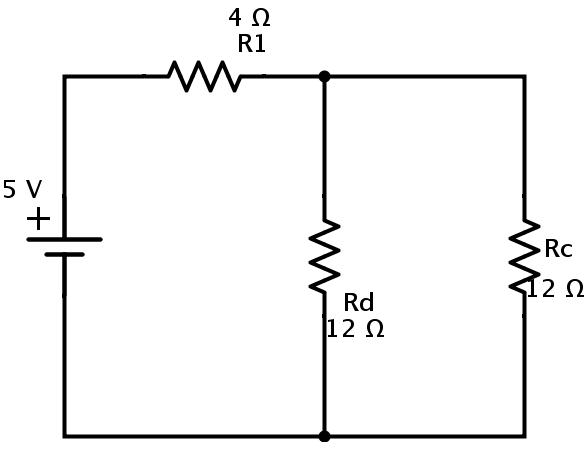
此处电阻Rc和Rd是并联组合的。设Rp是并联Rc和Rd的等效电阻。然后
Rp=(Rc×Rd)/(Rc+Rd)=(12×12)/(12+12)=6Ω.
得到的电路是
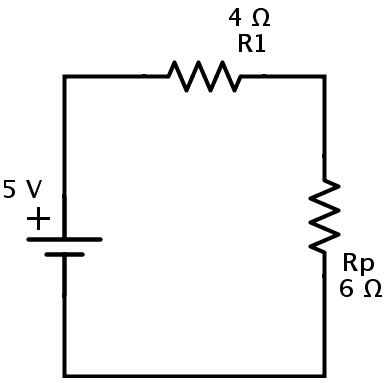
这里,电阻R1和Rp串联组合。让R情商是此组合的等效电阻。
然后
REQ=R1+Rp=4+6=10Ω.
这是电路的等效电阻。因此,给定的电路最终可以重新绘制为
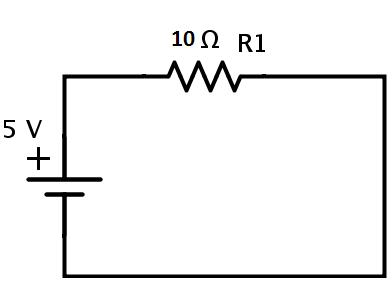
电路中的电流可以根据欧姆定律计算
I=V/REQ=5/10=0.5A
电阻器网络
我们来计算复杂电阻电路的等效电阻。
以下电路由十个电阻R1至R10组成,它们以串联和并联方式连接。
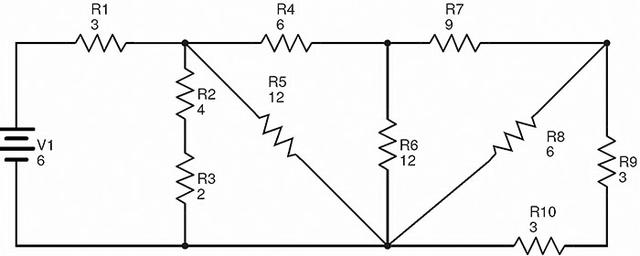
电路中提到的电阻值以欧姆(Ω)为单位,电源电压以伏特(V)为单位。
此处电阻R9和R10串联组合。让RA是此组合的等效电阻。
因此RA=R9+R10=3+3=6Ω.
用R替换R9和R10后的电路A是
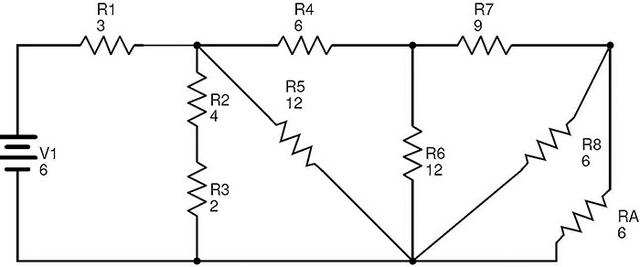
在该电路中,电阻R8和RA是并行组合的。那么R8和R的等效电阻A是
RB=(R8×RA)/(R8+RA)=(6×6)/(6+6)=3Ω.
现在取代R8和RA与RB,我们得到以下电路。
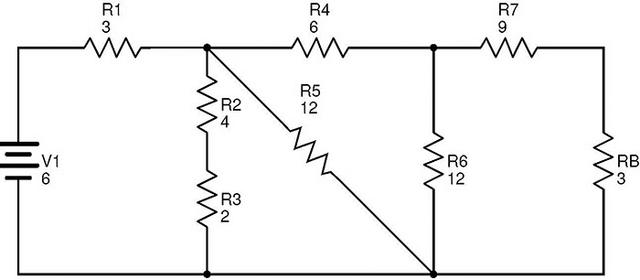
在该电路中,电阻R7和RB是串联组合。
RC=R7+RB=9+3=12Ω.
更换R7和R后的等效电路B与RC是
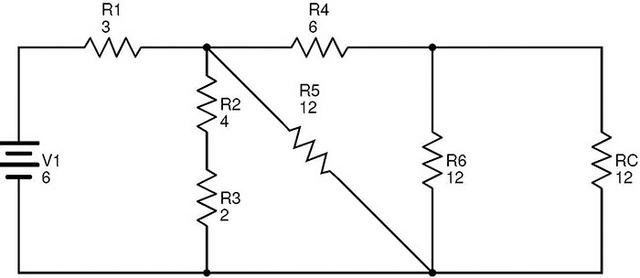
很明显,电阻R6和Rc是并联组合的。如果RD是这个组合的等效电阻,那么
RD=(R6×Rc)/(R6+Rc)=(12×12)/(12+12)=6Ω.
R¬D取代R6和Rc的电路是
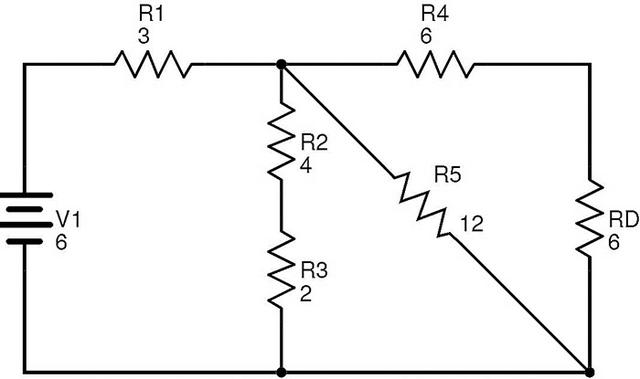
现在电阻R4和RD串联组合。如果RE是R4和RD的等效电阻,则
RE=R4+RD=6+6=12Ω.
更换R4和R后产生的电路减少D与RE是
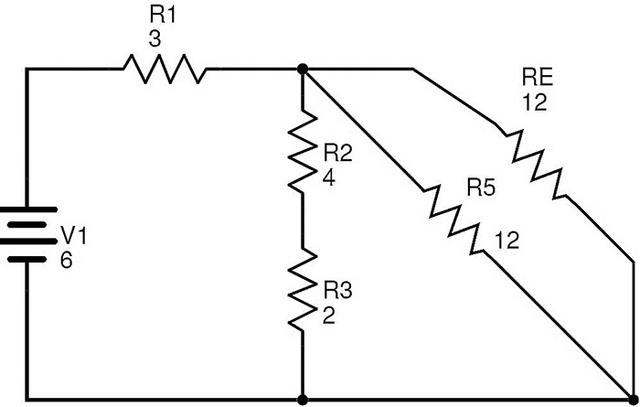
在该电路中,电阻R5和RE是并行组合的。
让RF是R5和R的等效电阻E并行。
RF=(R5×RE)/(R5+RE)=(12×12)/(12+12)=6Ω.
简化电路如下所示。
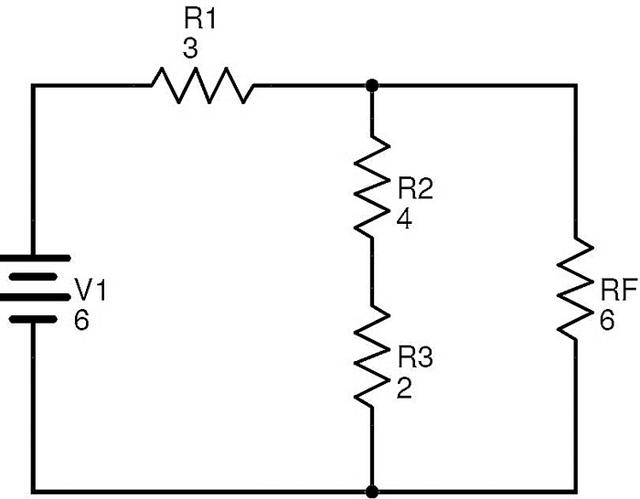
此处电阻R2和R3串联。如果RG等效于此组合,则
RG=R2+R3=4+2=6Ω。
用RG替换R2和R3后,电路将转换为
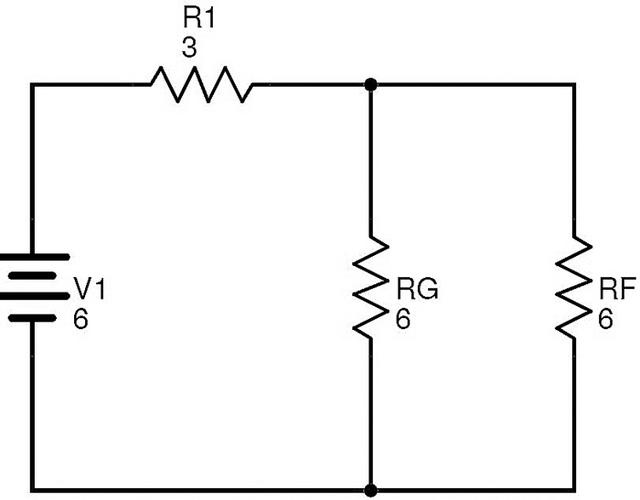
电阻RF和RG并联。
让RT等效于此组合。
然后RT=(RF×RG)/(RF+RG)=(6×6)/(6+6)=3Ω.
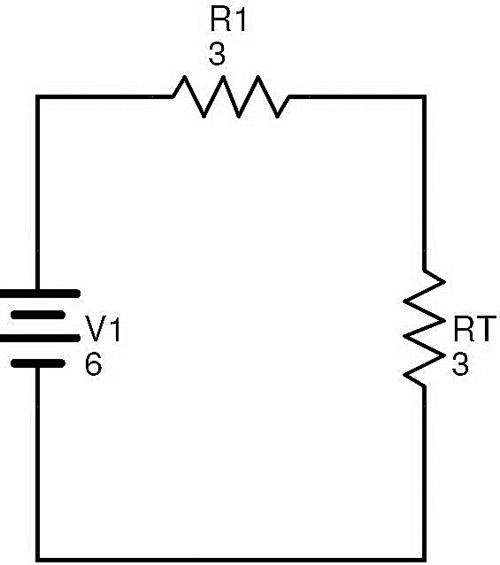
现在电阻R1和RT串联。如果REQ是总电路等效电阻,则REQ=R1+RT=3+3=6Ω。
最后可以按如下方式重绘上述复杂电路
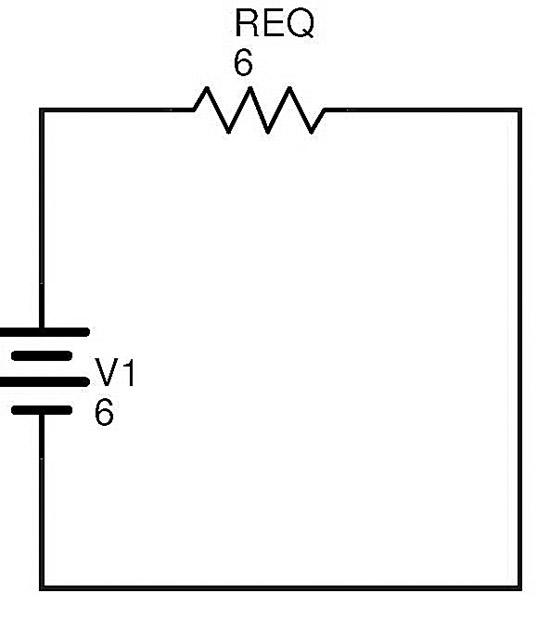
电路中的总电流可以使用欧姆定律计算
I=V1/REQ=6/6=1A
因此,通过首先识别简单的并联电阻支路和串联电阻支路,可以减少由串联和并联组合连接的电阻器数量组成的复杂电阻电路。计算这些简单分支的等效电阻,并将分支替换为等效电阻。这个过程降低了电路的复杂性。通过继续这个过程,我们可以用单个电阻器代替复杂的电阻电路。
有一些复杂的电阻电路不能通过简单地应用串联电阻组合和并联电阻组合的规则来简化为简单电路。T-Pad衰减器和一些复杂的电阻桥网络等电路就是这种复杂电阻电路的例子。为了简化这些复杂的电阻电路,需要采用不同的方法。
一些复杂的电阻电路可以通过使用基尔霍夫电流定律和基尔霍夫电压定律来减少。
仅使用欧姆定律来找到复杂电阻电路中的电流和电压可能是不可能的。对于这种类型的电路,基尔霍夫电路定律将有所帮助。
基尔霍夫电路定律基于电路中电流和能量守恒的概念。有两个基尔霍夫巡回定律。第一个是基尔霍夫电流定律,它处理节点上的电流,第二个是基尔霍夫电压定律,它处理闭合电路中的电压。
基尔霍夫电流定律指出:“进入节点的电流等于离开节点的电流,因为它没有其他地方可去,节点中也没有电流丢失。
简而言之,基尔霍夫电流定律指出,进入节点的电流总和等于离开电路的电流总和。
基尔霍夫电压定律指出,“闭环中的总电压等于该回路中所有电压降的总和。
简单来说,基尔霍夫电压定律指出闭环中电压的有向代数和等于零。
借助这两个定律,可以计算出任何复杂电路中的电流和电压值。
我们可能仍然有一些复杂的电阻电路,其中很难识别等效电阻,在这种情况下,我们将使用电阻器的星三角变换来简化电阻网络。
-
电阻器
+关注
关注
21文章
3827浏览量
62564 -
衰减器
+关注
关注
4文章
646浏览量
34584 -
电源电压
+关注
关注
2文章
993浏览量
24249 -
等效电阻
+关注
关注
7文章
60浏览量
11508 -
基尔霍夫电流定律
+关注
关注
2文章
27浏览量
8222
发布评论请先 登录
相关推荐




 串联和并联组合电阻器
串联和并联组合电阻器
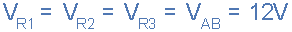











评论