为什么振荡器需要正反馈？LC振荡器如何实现自激式振荡呢？

一、概述

“振荡”（Oscillation），这个词其实就是指“往复运动”的意思。在电子学领域，电压、电流的来回波动，如我们熟悉的正弦波就是一种振荡。

由电容、电感构建的LC回路就能产生振荡。如下图，当开关由A切换至B，充满电的电容给电感充电，紧接着电感再给电容充电，如此往复。由于电路中不可避免的电阻会将电能消耗为热能，所以振荡波形随之衰减，直至消失。

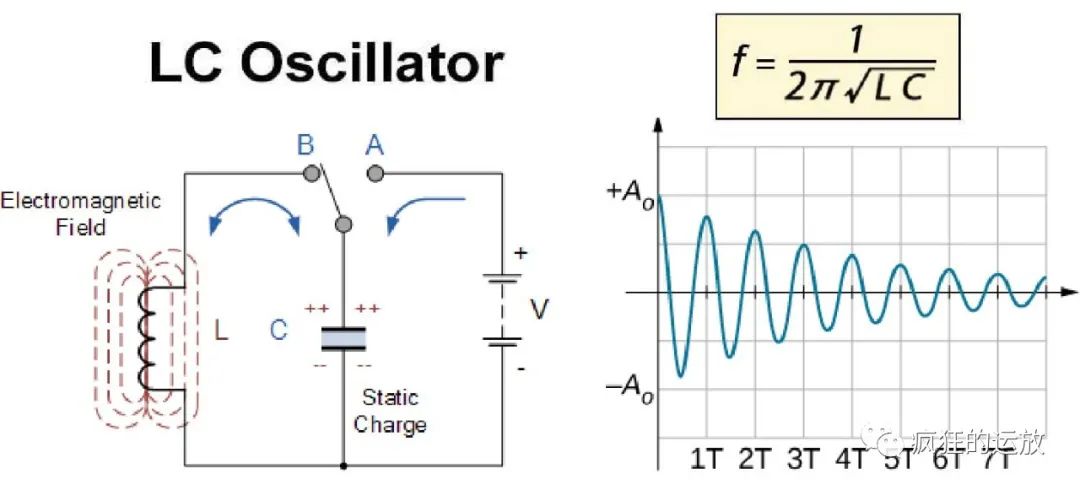
图1-LC振荡器的振荡波形衰减图

为了让振荡波形得以维持，必须采用某种机制，给LC回路源源不断补充能量，以抵抗电阻上的损耗，由此引出“振荡器模型”。

二、振荡器的“正反馈”模型

振荡器模型中有放大器、反馈网络两个模块，涉及的信号有输入信号Vin、反馈信号Vf和输出信号Vout：

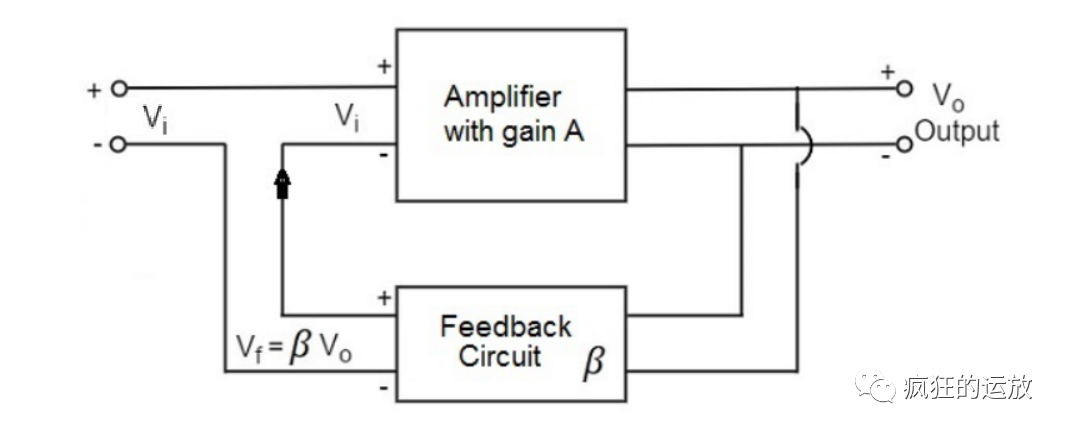
图2-振荡器的模型

先说明一下输入信号Vin是什么？输入信号其实是来自于热噪声（Thermal Noise），是由电子的热扰动引起的，存在于所有电子器件和导体中。虽然热噪声的信号非常微弱，但在频谱中以相同的形态分布（类似白噪声）。

也就是说，热噪声的频率成分非常丰富，这点很重要！如果我们要让振荡器工作在某个频率，只要不断地强化该频率上的成分，使其在热噪声中脱颖而出，这个过程就是“正反馈”。

正反馈的核心在于图2的“反馈网络”（Feedback），反馈网络首先是一个滤波器，它只选出感兴趣的频率成分，即“振荡频率”。其次，经过反馈网络的Vf，和Vin在振荡频率上的相位一致，两者叠加成为新的Vin再被送入放大器进行放大。每次反馈和放大，在振荡频率上，新的Vin都比前一次Vin要大，由此实现正反馈。

反馈网络可以由LC、RC、晶振等构成，对应不同的振荡器类型。特别的，对于LC振荡器模型（如下图），它的振荡频率就是LC回路的谐振频率，大小为1/(2π*(LC)(1/2))。这部分计算我们在之前详细讲过，有需要可以回顾一下。

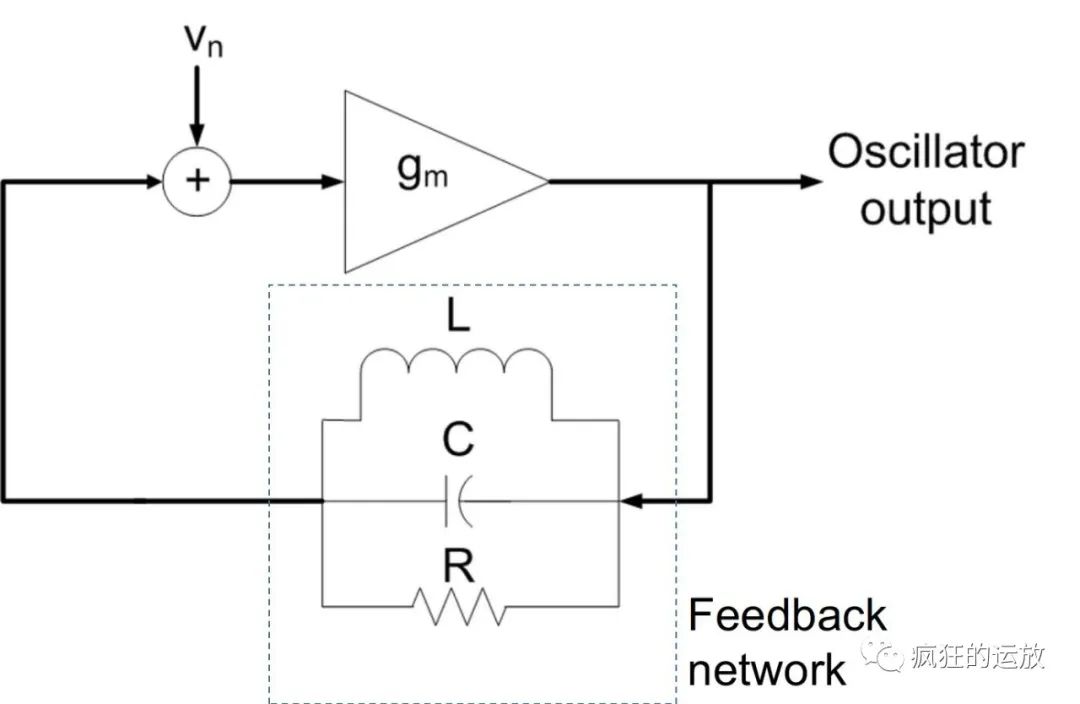
图3-LC振荡器模型

正反馈具体过程为：

1. Vin是热噪声，通过放大器后所有频率的信号成分都被放大，得到Vout，Vout=Av*Vin，其中Av是放大器增益；
2. 将Vout送入反馈网络，筛选出针对振荡频率的反馈信号Vf，Vf=β*Vout，其中β是反馈网络衰减比例；
3. 在振荡频率上，Vf与Vin相位一致，两者叠加成为新的Vin，再次送入放大器，以此循环；

三、Barkhausen（巴克豪森）准则

Barkhausen提出过一个振荡器准则，被认为是振荡器的必要不充分条件，奈奎斯特还对此修改过。此外，它使用的振动器模型稍有不同，所以在此不赘述公式，只简单介绍一下核心思想。

Barkhausen准则反映的是，振荡波形可能会衰减（由于增益不足或相位不一致），或递增（由于增益过高，但不会超过Vcc），只有当设计合理时，才会有稳定的波形：

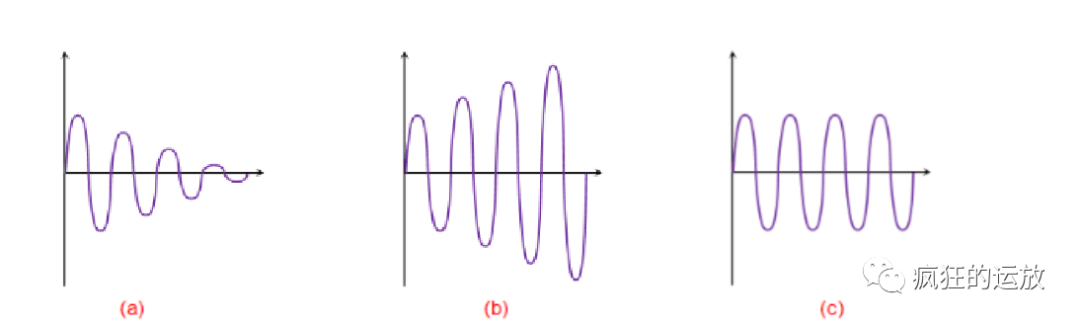
图4-Barkhausen（巴克豪森）准则描述振荡波形的三种情况

实际上，我们可以把振荡器的工作过程分成两个阶段：

• 在起振阶段，希望增益大一些，在输出端快速形成一定幅度的振荡波形；
• 在稳定阶段，增益可以小一些，在输出端获得幅度恒定的振荡波形；

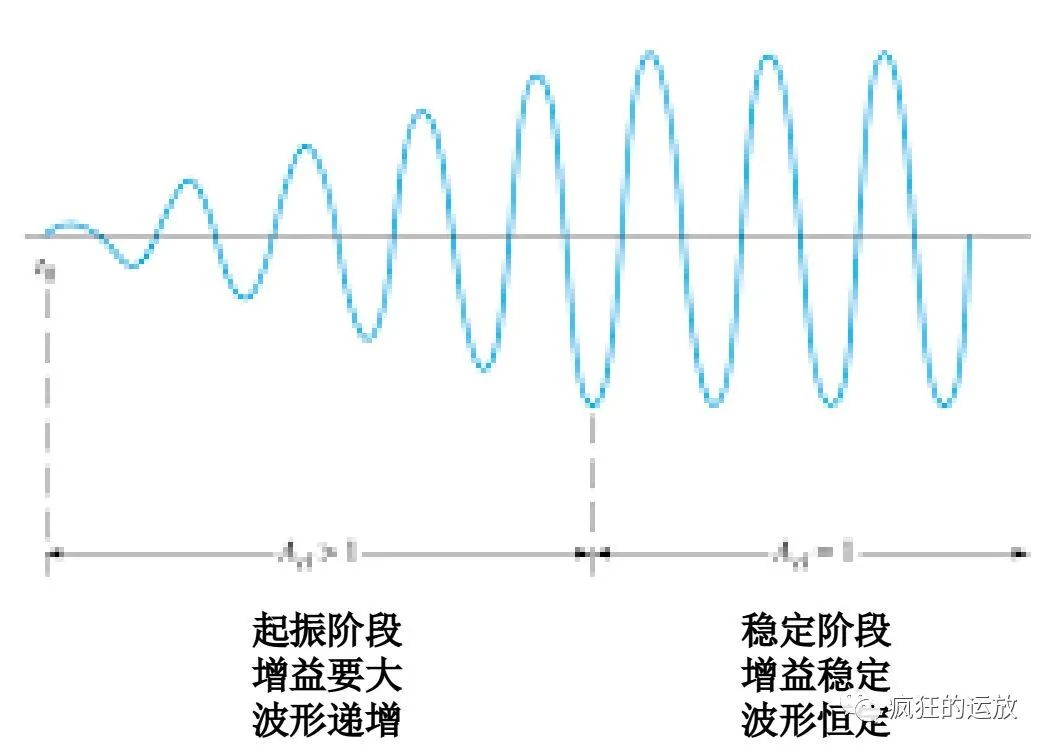
图5-振荡器的起振和稳定阶段

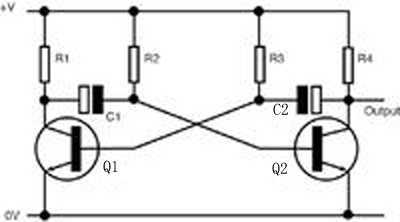
四、LC自激振荡器（电容和电感三点式振荡电路）

基于LC回路的反馈网络有两个基本的振荡器，都是利用热噪声的“正反馈”自己产生振荡，称为“自激振荡器”。

一个是利用两个电感（或一个电感中间抽头）的分压进行反馈，称为Hartley（哈特莱）振荡器或电感三点式振荡器：

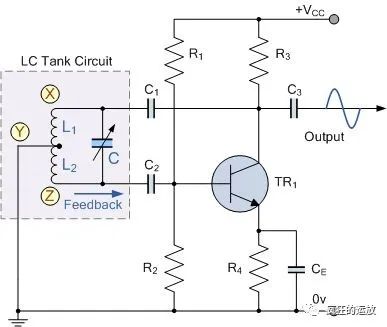
图6-Hartley（哈特莱）振荡器/电感三点式振荡电路

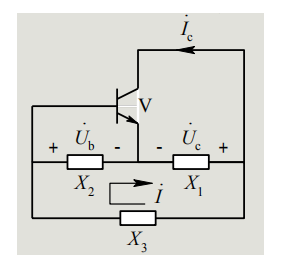
另一个是利用两个电容的分压进行反馈，称为Colpitts（考毕兹）振荡器或电容三点式振荡器：

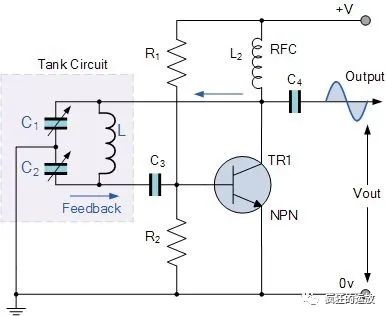
图7-Colpitts（考毕兹）振荡器/电容三点式振荡电路

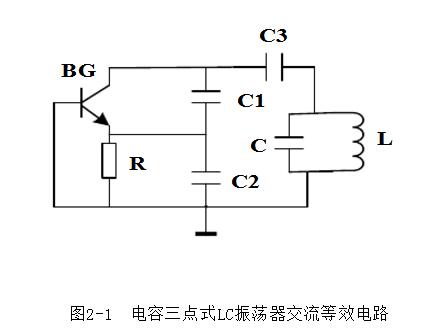
相位上，输入信号/反馈信号同是Z->Y两端，输出信号是X->Y两端，两者相位反向。但由于三极管是集电极输出，输入信号经过放大后与输出信号相位一致。

增益上，起振时，三极管的增益是大的。随着振荡幅度增大，R4上电压上升（由RC滤波），使三极管B-E两端电压降低，这会降低三极管增益，以此实现增益自动调整，维持稳定的振荡幅度。

振荡频率，计算简单，即为LC回路构成的谐振频率。

振荡幅度，计算复杂，可以通过仿真软件来计算结果。

五、总结

今天学习了LC振荡器，它利用了正反馈机制，实现了自激式振荡。